基于PSO算法的GMM改进J-A磁滞模型的参数辨识与验证

滕峰成，王珊珊，杨雪璠，吕登岩

(燕山大学 电气工程学院，河北 秦皇岛 066004)

1 引 言

电力设备的安全在线监测在电力系统安全、经济、稳定的运行中起着至关重要的作用。其中电流检测技术的精确度和可靠性直接影响继电保护系统的运行，而传统的电磁式电流互感器已难以满足电网发展的需求[1]。光学电流传感器以其抗电磁干扰能力强、绝缘性能好、耐高温、耐腐蚀等优点，非常适用于环境复杂的电力系统中[2]。超磁滞伸缩材料(giant magnetostrictive material，GMM)具有频响速度快、能量转换率高等优点，广泛应用于各种驱动和换能领域[3，4]；光学材料中的光纤布拉格光栅(fiber bragg grating，FBG)线性响应好、机械强度高、动态范围宽，可靠实用[5]。GMM-FBG电流传感器将GMM和FBG结合起来作为传感单元进行电流测量。然而，GMM作为一种铁磁性材料，本身固有的磁滞非线性会影响电流传感器的输出，降低系统传感精度。因此，需要建立准确的GMM磁滞模型。

近年来，J-A理论基于材料的物理特性从磁畴机理和能量变化的角度阐述了磁滞特性，被广泛用于铁磁材料的磁滞建模中[6～10]：文献[9]提出了一种动态J-A模型，并以330 kV P级电流互感器为例，搭建了大通流的动态模拟试验平台，验证模型的可靠性；文献[10]采用了人工鱼群与Levenberg-Marqardt混合算法对J-A模型进行了参数辨识，但是实验只能用于频率5 Hz以内的情况下。

为减小由磁滞引起的测量误差，提高GMM-FBG电流传感器的测量精度，本文基于经典的J-A磁滞模型提出了改进的适用于低频条件下的J-A模型。采用粒子群(particle swarm optimization，PSO)算法对模型的参数进行辨识及优化，搭建了相应的GMM-FBG电流传感系统实验平台，并对实验结果与仿真结果进行了对比分析。

2 GMM-FBG电流传感器模型

GMM-FBG电流传感器的原理是：当交变电流产生时，驱动线圈感应产生相应的驱动磁场，置于磁场中的超磁致伸缩材料(GMM)被磁化，产生纵向伸缩现象。由于GMM在交变磁场中会产生磁滞损耗，因此磁场与应变之间是滞回非线性的关系。GMM通过胶粘剂与光纤光栅(FBG)相连，使其中心波长发生漂移。GMM-FBG电流传感器工作时，光纤光栅的波长信号为连续采集量，且波长变化呈现正弦变化规律。同时，光纤光栅波长的周期变化与GMM的磁滞回线的变化为一一对应的关系，因而识别光纤光栅波长的正弦周期变化即可识别GMM磁滞回线的具体变化，进而计算出其线圈电流的瞬时值，实现测量。

电流传感器的模型是由驱动磁场的产生部分、GMM的形变部分和FBG的波长偏移部分组成，模型见图1所示。

图1 GMM-FBG传感模型Fig.1 GMM-FBG sensing model

(1) 驱动磁场强度

在磁路闭合的情况下，不考虑漏磁，向驱动线圈中通入电流，产生相应的驱动磁场H为：

H=NIsin(2π ft+φ)+Hb

(1)

式中：N为单位长度线圈匝数；I为激励电流幅值大小；f为驱动频率；φ为初相角；Hb为偏置磁场强度。

(2)GMM的应变量模型

GMM由驱动磁场作用产生的磁化强度M可以表示为：

(2)

式中：μ0为真空磁导率；B为磁感应强度。

磁致伸缩棒处于磁场中产生的相应的形变量ε为：

(3)

式中：ΔL为棒的伸长量；L为棒的长度；f(M)为与磁化强度相关的函数。

考虑磁滞效应和预应力的影响时，形变量ε与磁化强度M关系为：

(4)

式中：EH为固定磁场强度下的杨氏模量；σ为外加预应力；λs为饱和磁致伸缩系数；Ms为饱和磁化强度。

(3)FBG中心波长偏移量与应变的关系

假设胶粘剂的性能良好，GMM的应变量将完全作用于光纤光栅，当温度不变时，光栅波长的相对变化量ΔλB与施加的纵向应变ε成比例：

(5)

式中Pe为有效光弹系数。

综上，可得光栅波长偏移量与输入电流的关系为：

(6)

由于GMM存在磁滞效应使得输出波长的偏移量与磁场强度之间出现滞回非线性，测得的波长不能完全反应输入电流的特征，引起误差。为消除磁滞效应的影响，需要对GMM进行磁滞建模补偿。

3 改进J-A磁滞模型

3.1 经典J-A模型

J-A磁滞模型建立的基础是铁磁材料的磁畴运动理论，由于磁畴的结构和受力等因素的不同，使得铁磁材料在磁化过程中磁畴的移动和旋转过程不可逆，从而形成磁滞并产生能量损耗[8]。Jiles和Atherton在对磁畴运动研究的基础上共同提出磁化过程分为可逆磁化阶段和不可逆磁化阶段，并以微分方程的形式描述了两个阶段的微分磁化率，最终获得磁化强度与激励磁场强度之间的滞回非线性关系。

在J-A模型中，将总磁化强度M表示为可逆磁化强度Mrev和不可逆磁化强度Mirr之和：

M=Mrev+Mirr

(7)

根据Boltzman原理，完全可逆的无磁滞磁化强度Man为：

(8)

式中：He为有效外加磁场；a为无磁滞磁化强度的形状参数。

磁性材料所受的有效外加磁场He：

He=H+αM

(9)

式中：H为外加磁场；α为磁畴相互作用系数；αM为材料内部磁畴间相互作用产生的磁场。

无磁滞磁化强度Man，不可逆磁化强度Mirr和可逆磁化强度Mrev的关系为：

Mrev=c(Man-Mirr)

(10)

式中c为可逆系数。

不可逆磁化强度为Mirr：

(11)

通过联立式(7)～式(11)，可获得J-A磁滞模型的主方程：

(12)

微分方程(12)表示磁化强度M和磁场强度H之间的关系。Ms、α、a、k、和c这5个参数共同确定了J-A磁滞模型。因此只要确定了GMM励磁特性的这5个参数，便能得到标准的J-A磁滞模型。

但是经典的J-A磁滞模型没有考虑材料的磁机耦合特性、涡流损耗等因素，因此只适用于静态条件下[11]。

3.2 改进J-A磁滞模型

鉴于本文所设计的GMM-FBG电流传感器应用于工频条件下检测交流电流，即准静态条件下，所以经典J-A磁滞模型无法满足GMM-FBG对传感精度的要求，故提出可用于低频磁化条件下的改进J-A磁滞模型。

根据式(9)可知，有效磁场He是由驱动磁场H和磁畴间相互耦合的平均磁场αM组成。当GMM受到机械应力的作用时，内部的磁化也会受到影响，产生磁机耦合的现象。考虑到材料的磁机耦合特性，对力-磁-热多场耦合的GMM非线性本构模型[12]进行简化，忽略温度的影响，得到：

(13)

式中：χm为磁化曲线初始阶段的磁化系数;λs为饱和磁滞伸缩系数；σs为饱和应力。

此处可将有效磁场He修正为：

(14)

根据式(7)，可以得到如下微分方程：

(15)

将式(10)代入式(15)，化简可得：

(16)

当H=(Man-Mirr)<0时，J-A模型会产生负的磁化系数，为防止此现象产生，在此引入参数ξ：

ξ=0.5[1+sgn(H=(Man-Mirr))]

(17)

则总的磁化微分方程变为：

(18)

式(14)～(18)考虑了材料的磁机耦合特性，但没有包含动态磁化时的涡流效应和额外损耗，因此这样建立的磁滞模型只适用于低频磁化条件下。

4 基于PSO算法的参数辨识及优化

4.1 PSO算法

PSO算法最早由Kennedy和Eberhart于1995年提出，该算法模仿鸟类觅食行为，将每只鸟抽象为一个粒子，由初始粒子的适应度值确定个体极值和群体极值，在每次迭代过程中，更新粒子速度和位置，算法所寻找的最优解即等同于鸟类寻找的食物[13]。粒子群算法具有群体智能、迭代格式简单、收敛速度快等优点[14，15]，因而广泛应用于函数优化领域。

4.2 适应度函数

根据最小二乘法，设函数为：

(19)

式中:ym(t)为改进J-A模型中磁化强度的计算值；y(t)为磁化强度的实验值;t为连续采样时间。

实际应用中，采用离散时间n代替连续时间t，适应度函数变为：

(20)

将适应度函数E(θ)作为目标函数，求目标函数的最小值。适应度值越小，改进J-A磁滞模型的预测值与实验值误差越小，个体越优。

4.3 PSO算法参数影响的分析

在PSO算法中，种群数目m，迭代次数T，惯性权重w1、w2，加速度因子c1、c2对算法精度、运行速度均有影响。因此，要分析各参数对算法的影响。

4.3.1 种群数目m对算法的影响

令T=200，w1=0.8，w2=0.3，c1=c2=2。取不同的m值，每个值对算法运行10次，取预测数据和实验数据的平均误差eave，运行结果见表1。由运行结果可知：算法的误差在种群数目为400时基本不变。因此，选择m=400作为算法的运行参数。

表1 种群数目m的影响Tab.1 Impact of population number m

4.3.2 迭代次数T对算法的影响

令m=400，w1=0.8，w2=0.3，c1=c2=2。取不同的T值，每个值对算法运行10次，取预测数据和实验数据的平均误差eave，运行结果见表2。由运行结果可知：算法的误差在迭代次数为100时基本不变。综合考虑，可取T=150作为算法的运行参数。

表2 迭代次数T的影响Tab.2 Impact of the number of iterations T

4.3.3 人惯性权重w1，w2对算法的影响

令m=400，T=150，w2=0.3，c1=c2=2。取不同的w1值，每个值对算法运行10次，取预测数据和实验数据的平均误差eave，运行结果见表3。由运行结果可知：算法的误差在种惯性权重w1为0.7附近时最小。因此，选择w1=0.7作为算法的运行参数。

表3 惯性权重w1的影响Tab.3 Impact of inertia weight w1

令m=400，T=150，w1=0.7，c1=c2=2。取不同的w2值，每个值对算法运行10次，取预测数据和实验数据的平均误差eave，运行结果见表4。由运行结果可知：算法的误差在种惯性权重w2为0.4附近时最小。因此，选择w2=0.4作为算法的运行参数。

表4 惯性权重w2的影响Tab.4 Impact of inertia weight w2

4.3.4 加速度因子c对算法的影响

令m=400，T=150，w1=0.7，w2=0.4。设c1=c2=c，取不同的c值，每个c值对算法运行10次，取预测数据和实验数据的平均误差eave，运行结果见表5。由运行结果可知：算法的误差在种加速度因子c为2.5附近时最小。因此，选择c1=c2=2.5作为算法的运行参数。

表5 加速度因子c的影响Tab.5 Impact of acceleration factor c

综上所述，选取m=400，T=150，w1=0.7、w2=0.4，c1=c2=2.5为算法的最佳参数组合，得到的参数辨识结果见表6。PSO适应度曲线见图2。

表6 模型参数辨识结果Tab.6 Model parameter identification result

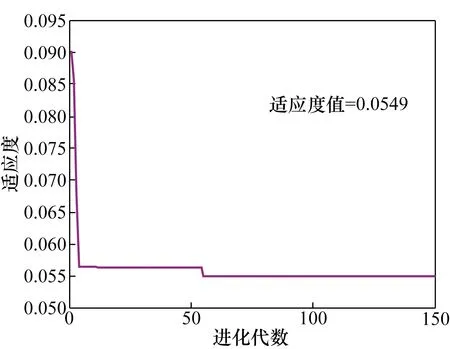
图2 PSO算法适应度曲线Fig.2 PSO algorithm fitness curve

应用改进后J-A模型进行预测，模型预测仿真结果见图3所示，相应的误差曲线见图4中蓝色线条所示。在工频的驱动下，改进后模型能较好地预测实际滞回曲线，模型误差在5.5%以内。

图3 改进后模型仿真与实验对比及误差明显部分Fig.3 Comparison diagram of Improved model simulation and experimental and obvious part of the error diagram

图4 改进后模型与分段模型误差图Fig.4 Error diagram of Improved model and segmented model

4.4 分段变系数模型的建立及参数优化

观察改进后J-A模型预测仿真结果图，可发现图形中间部分预测值大多小于测量值而两端部分预测值大多大于测量值，严重影响了模型精度，于是提出将模型分段进行参数识别。采取同上文的采样方式，即1个周期内有40个采样点，对其按照时间顺序分为[1～7]、[8～16]、[17～27]、[28～36]、[37～41]5部分，其中[1～7]、[17～27]、[37～41]为1组，记为①;[8～16]、[28～36]为另1组，记为②;分别进行参数识别，分段形式见图5。分段辨识结果见表7，分段模型在PSO算法下的适应度曲线见图6。

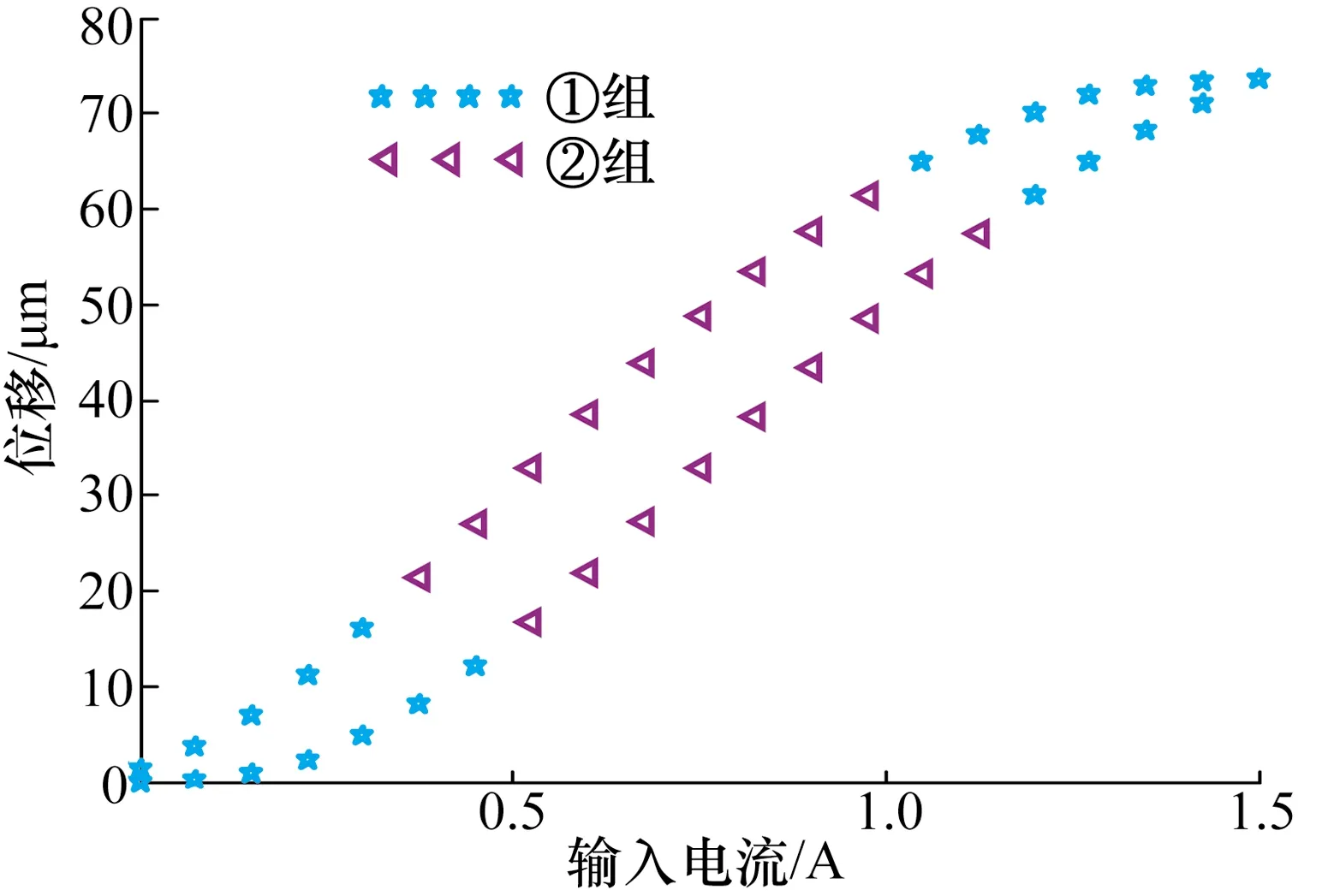
图5 分段形式图Fig.5 Segmentation diagram

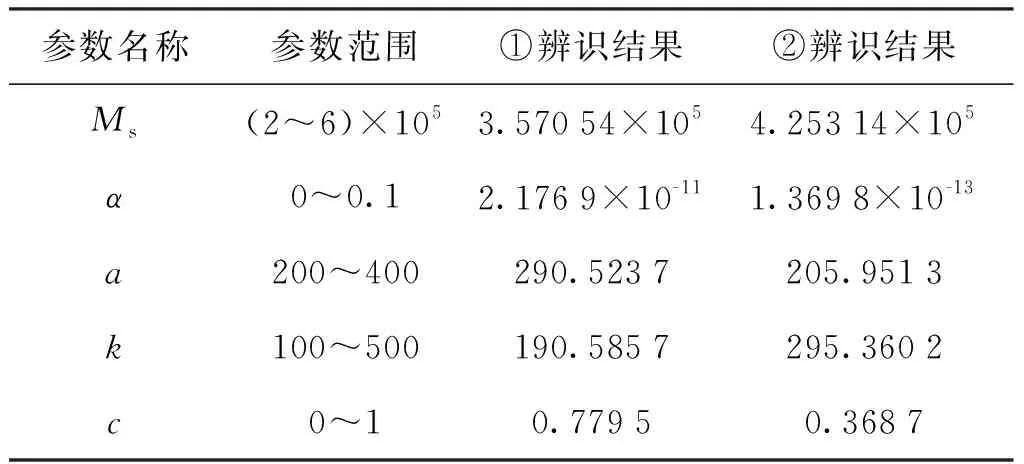
表7 分段模型参数辨识结果Tab.7 Segmented model parameter identification result

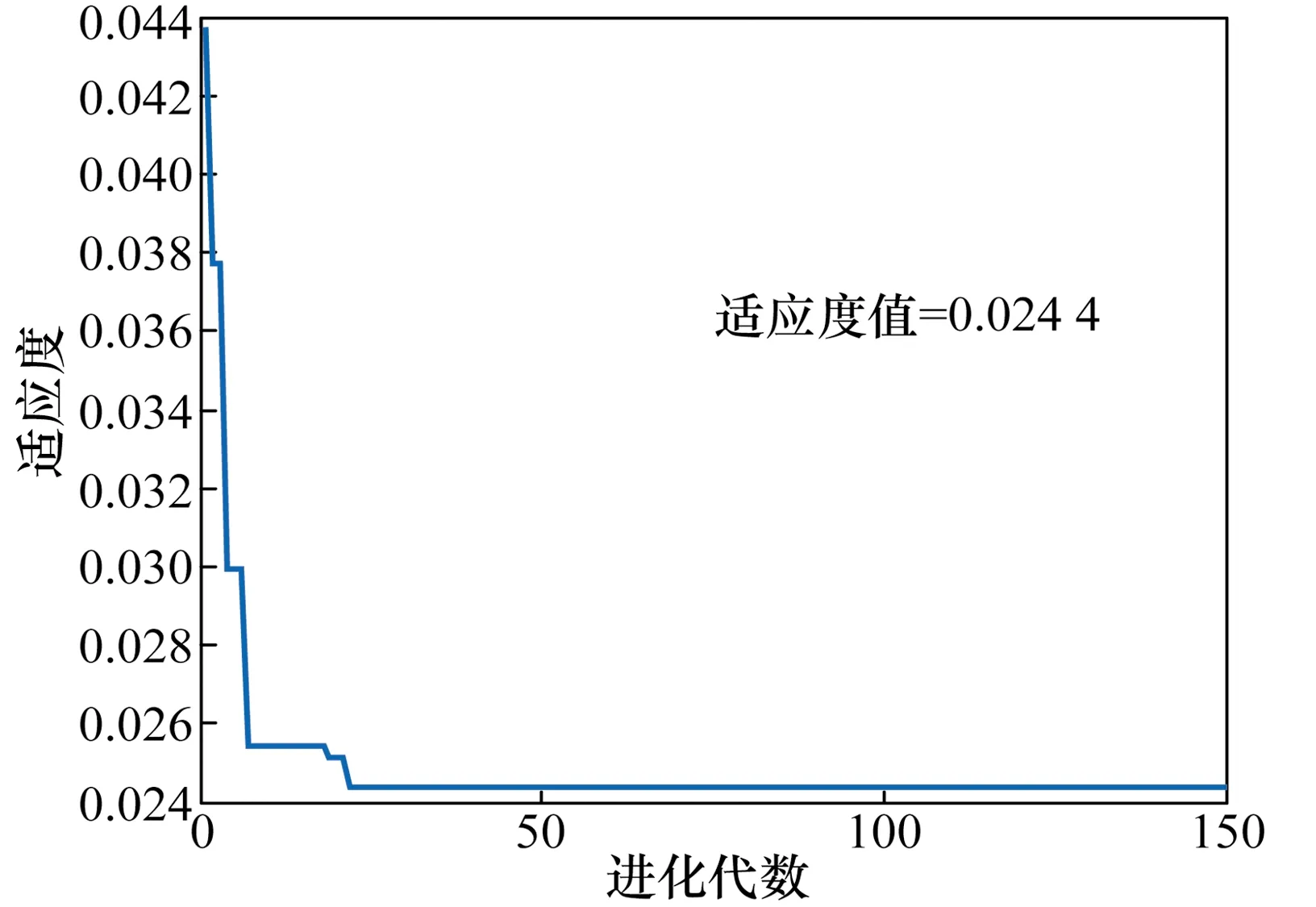
图6 分段模型在PSO算法下的适应度曲线Fig.6 PSO algorithm fitness curve of segmented model

应用分段模型进行预测，预测仿真结果见图7所示，相应的误差曲线见图4中红色线条所示。图4为改进后模型与分段模型误差对比图，由图可见：模型分段后预测值与测量值的误差明显小于分段前，平均误差由5.5%减小到2.5%以内，提高了模型的预测精度。分段后模型预测值与测量值之间相符度良好，能更好地预测实际的滞回曲线。

图7 分段模型仿真与实验对比图Fig.7 Improved model simulation and experimental comparison diagram

5 实验分析

为验证改进模型的有效性，获取实验数据，搭建了交流传感系统试验台，其示意图见图8所示。系统主要分为两大部分，即测量部分和解调部分，两部分之间通过FC/APC连接器相连。图中，交流驱动源提供50 Hz下幅值可调节的激磁电流，直流电源产生直流偏置磁场，FBG波长解调仪测量光纤光栅输出的中心波长的偏移量。

图8 GMM-FBG交流传感试验台示意图Fig.8 GMM-FBG AC sensor test bench diagram

实验中GMM采用的是尺寸为φ5 mm×30 mm的TbDyFe(T-D)棒，其饱和磁致伸缩系数λs为 1 263×10-6。 用环氧树脂胶将FBG粘贴于T-D棒上，并且对T-D棒施加10 MPa的预应力。该T-D棒在10～60 kA/m的磁场强度范围内线性度较好，因此应保证施加在GMM上的磁场强度在该线性范围内。针对温度对测量结果有交叉影响的问题，采用在T-D棒与励磁线圈间加隔热层的方法，同时采用基于2×2和3×3的非平衡马赫-泽德干涉仪，可以解决温度与测量交叉敏感的问题[16]。

驱动线圈施加50 Hz下的交流电流，调节调压器，使电流从0逐次增大到3 A，每次增大0.5 A。通入交流电流对应波长偏移曲线如图9所示。当给激磁线圈通入3 A的正弦交流电时，数据采集系统同步检测到的输入电流信号和波长偏移信号如图10所示,由从图可以看出输入波长信号上宽下窄，这是由于GMM磁滞特性的存在而出现的滞回现象。

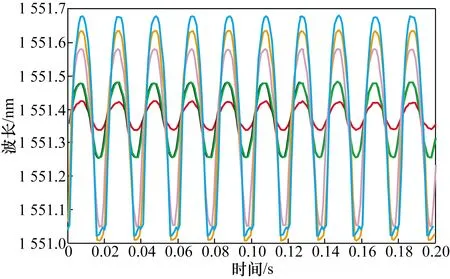
图9 不同交变电流对应的波长偏移曲线Fig.9 Wavelength shift diagram corresponding to different alternating currents

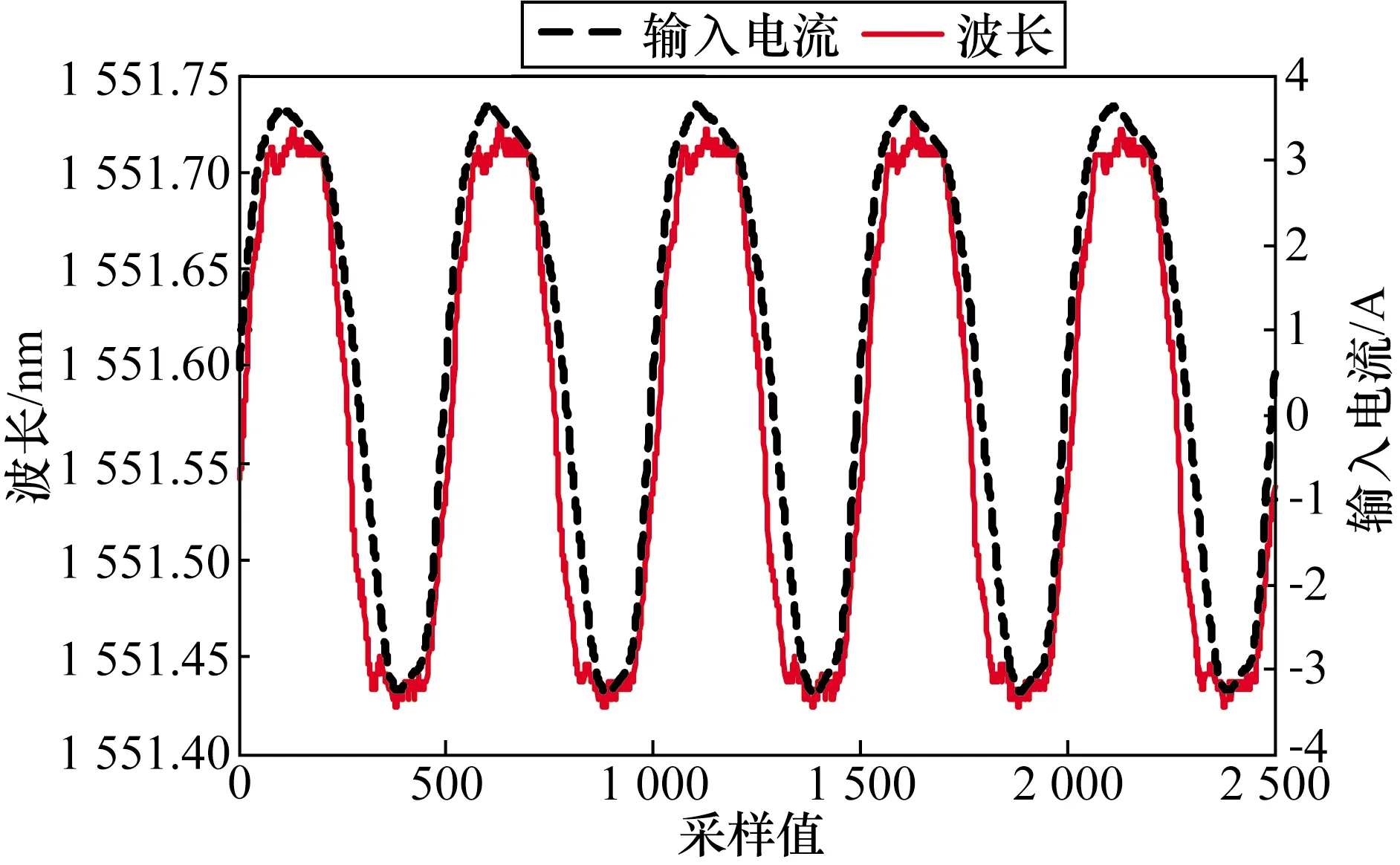
图10 电流与波长对比图Fig.10 Current and wavelength contrast diagram

恒温条件下保持偏置磁场不变，向驱动线圈中通入幅值为3 A的工频交流电流，获得传感器的滞回曲线。分别用经典J-A模型和改进的分段J-A模型对系统的滞回进行模型预测，并得到相应的预测曲线。模型预测曲线与实测曲线对比如图11所示，模型预测误差曲线如图12所示。由图可以看出，在同样通入幅值为3 A的工频交流电流时，改进J-A模型能更好地预测滞回曲线，模型最大预测误差由经典J-A模型的0.45 nm减小至0.1 nm，具有良好的预测能力。经过实验验证，应用改进J-A模型的系统具有良好的输出特性，系统输出能够基本准确地反映被测电流信息，传感系统电流测量灵敏度为0.067 nm/A，最小可测量的交流电流为0.1 A。

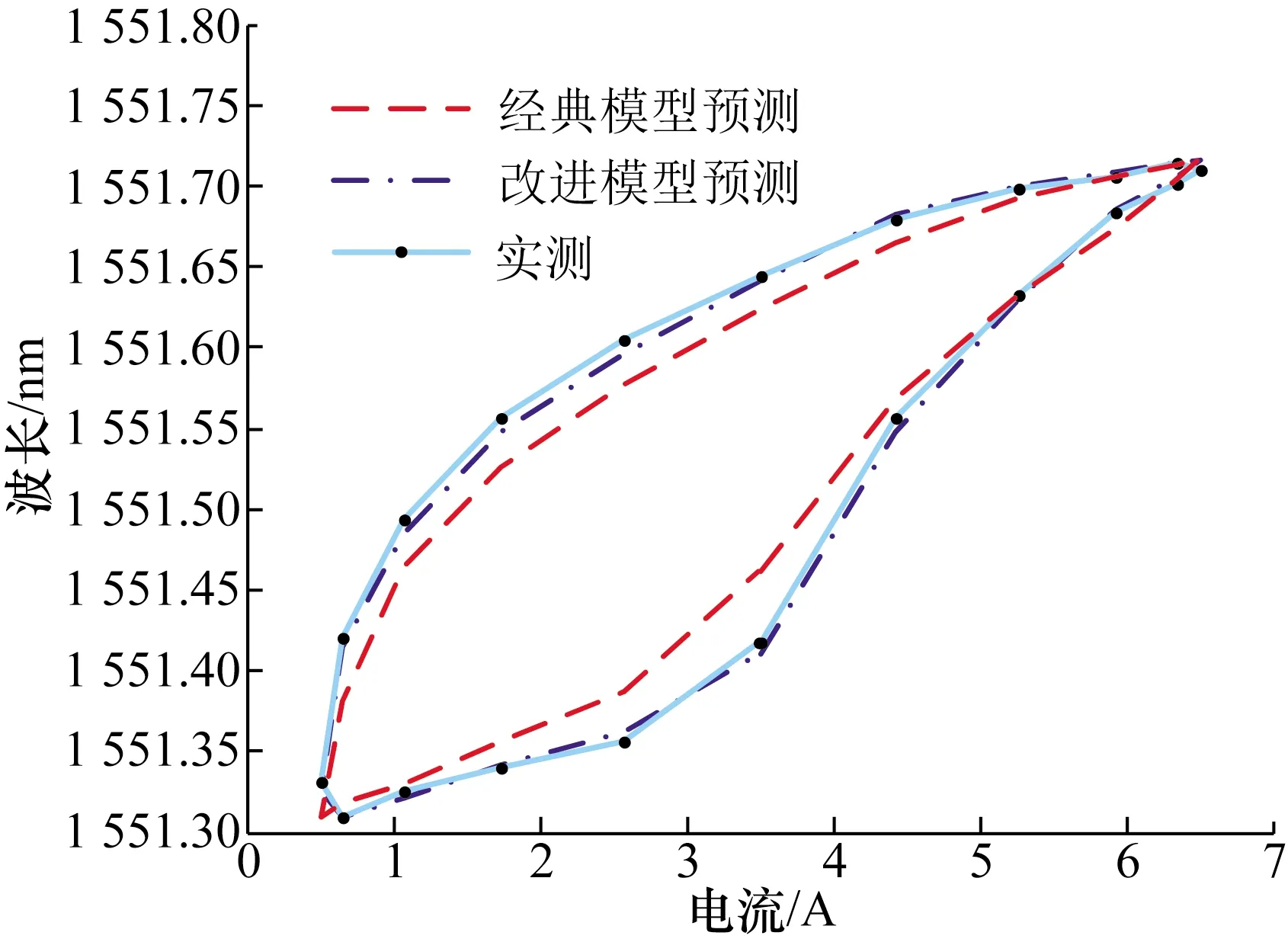
图11 模型预测与实测对比图Fig.11 Model prediction and measured contrast diagram

图12 模型预测误差曲线图Fig.12 Model Prediction Error diagram

6 结 论

为解决GMM-FBG交流电流传感器的磁滞非线性问题，提出了一种改进的J-A磁滞模型。采用PSO算法进行参数的辨识及优化，结合模型的具体情况，提出了分段变系数的方法对模型进行分段辨识。搭建了相应的GMM-FBG交流传感系统实验平台，并运用改进后的J-A模型进行了仿真预测，验证了模型的可靠性。实验及仿真结果表明：改进后模型的误差小于2.5%，电流的测量灵敏度为0.067 nm/A，最小可测量的交流电流为0.1 A。