实正则方形代数系统

徐 嘉

(西南民族大学数学学院，四川 成都 610041)

非线性代数系统求解是计算代数中的基本问题.这个问题出现在了需要处理多项式方程的符号和数值技术当中.作为表示或约束，在计算机代数，鲁棒分析，几何造型的应用中使用了大量的多项式方程[1-2].然而众所周知，一般情况下非线性代数系统是无法求出所谓"精确解"的.退而求其次，零点的隔离被当作是代数系统的精确解的替代(代数系统的解常常也称为零点).在代数系统的自身结构研究以及应用方面，零点的隔离起到了基本的作用.本文中我们主要研究实系数方形代数系统实零点的隔离.

方形代数系统是指变元个数与方程个数相同的代数系统.隔离代数系统的实零点就是寻找一系列互不相交的Box(区间的直积)，每个Box内精确地包含一个零点.系统

在空间ℝn中的一个零点x*，如果满足Jacobian矩阵Jf(x*)是非奇异的，则称x*是实正则零点.我们还需要进一步的假设给定的系统仅仅只有有限个实正则零点.对非正则零点的处理可参考文献[3]，本文不多涉及.

有许多的方法可以被应用到代数系统实零点的隔离.一种较常用的思想是将原始系统转化为三角列形式，再对三角列进行零点隔离.被使用的消去工具有Groebner基方法[4]，吴方法[5]，正则列方法[6]等等.但是消去过程往往需要大量的符号计算，导致效率不高.这些方法都各有自身特点和优点.

本文的方法主要使用Dixon结式[7-8]和伴随多项式方法[9].在第1节，简单地介绍了Dixon结式，以及怎样去获得初始的Box，使得给定系统的所有实正则零点都位于这些Box中.第2节，首先介绍了伴随多项式的概念，总结了伴随多项式的4个基本性质.接着给出了如何检测初始的Box中是否存在给定系统的零点的方法.第3节，建立了一个隔离代数系统实正则零点的算法SAS-Zeros.

1 Dixon结式

1779年，Bezout研究了计算两个单变元多项式的结式.它是用较低阶(相对于Sylvester行列式)的行列式来表示结式.下面的构造方法是由Cayley给出的.

给定两个d次多项式f(x)，g(x)，行列式

是关于x和α的多项式.注意到当x=α时D(x，α)=0.

因此，

是关于α的d-1次多项式.即

这里ci(x)是关于x的≤d-1次多项式.如果x0是f(x)和g(x)的公共零点，则D(x0，α)=0对任意α，这蕴含了

很明显(1)是关于d个变元x0，…，xd-1的线性方程组.这个方程组有非平凡解，因为x0=1.所以其系数矩阵的行列式为0.这个行列式就是著名的Bezout结式.

1908年，Dixon推广了这个思想.构造了一般的Bezout结式.Dixon[7]的工作之后，人们逐渐发现Dixon结式在较大范围的情况是奇异的，也就是res(f1，…，fn)恒等于0，因此得不到关于原方程组的有用信息.

一个重要的进展发生在1994年，D.Kapur，T.Sexena，Lu Yang(杨路)在文献[8]中建立著名的KSY条件，并给出计算Dixon结式的高效率算法.

Dixon结式的基本用法是消元，即从k+1个方程中消去k个变元.对给定的方形系统，Dixon结式在本文中的主要作用是获得单个变元的多项式.

下面看个例子.

例1[12]给定代数系统

第一步:将系统看作变元x2，x3，x4的系统，计算其Dixon结式，我们得到关于x1的多项式(相当于消去了变元x2，x3，x4).

完全类似的，可以得到另外三个单变元多项式

系统(2)的一个解需要满足上面的四个单变元多项式.

第二步:分别对上面的四个单变元多项式做实根隔离[1]，获得隔离区间集(区间长度可选择).

第三步:依次从集合S1，…，S4中各取一个区间作直积，我们就获得了由54个Box组成的集合SB.如果用1，2，3，4，5的一个可重复排列作下标来表示这些Box，例B1111表示依次从S1，…，S4取第一个区间所获得的Box，就是

于是SB={Bi1，i2，i3，i4}.系统(2)的所有实正则零点都位于这些Box中，并且每个Box中至多有一个零点.剩下的工作就是判断SB中哪些Box有系统的零点，哪些没有.这个问题的回答构成了下一节的主要内容.

2 伴随多项式与实正则零点的检测

2.1 伴随多项式与无实零点的检测

给定BoxB=[a1，b1]×…×[an，bn]和实系数方形代数系统

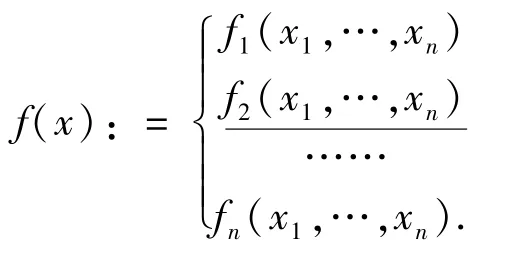
一个基本的问题是:f(x)=0在BoxB上是否存在零点?本文的方法主要依赖于下面的伴随多项式概念.

定义[9]多项式f∈ℝ[x1，…，xn].f相对于变元xi次数记为di(i=1，…，n)对BoxI=[a1，b1]×…×[an，bn]， 我们定义

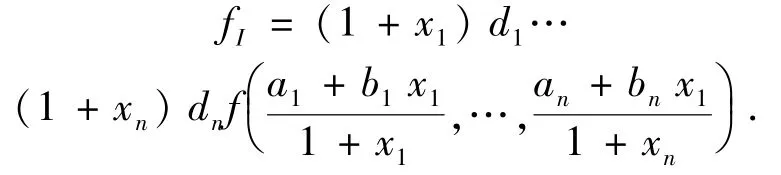
fI称为f相对于BoxI的伴随多项式.

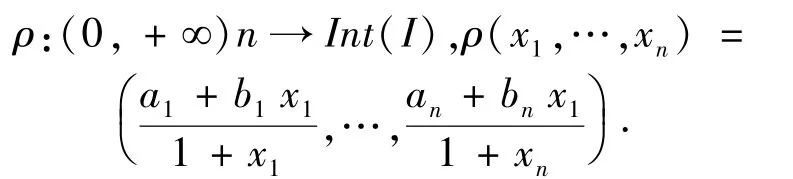
注意到映射是一一映射.这里Int(I)是指BoxI的内部.

下面总结了部分伴随多项式的基本性质，证明都非常简单.

伴随多项式的基本性质

①如果fI的所有非零系数都是正(负)数，则

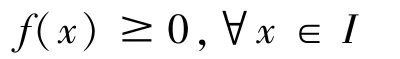
②多项式f在BoxI内部Int(I)存在零点，当且仅当fI在(0，+∞)n上存在零点.

③如果fI的所有非零系数都是正(负)数，则多项式f在BoxI内部Int(I)没有零点.

④如果fI的所有非零系数都是正(负)数且f在BoxI的所有顶点上的值都不是0，则多项式f在整个BoxI(包括内部和边界)上没有零点.

这些性质虽然简单，但应用却非常广泛.比如根据性质④可以容易地证明代数系统在给定的Box上没有实解.

在文献[9]中证明了如下结果，它显示了用伴随多项式方法检测代数系统(不一定是方形的)无实零点是完全的方法.

定理1设多项式f1，…，fm∈ℝ[x1，…，xn]，BoxΛ⊂ℝn.方程组f1=0，…，fm=0在BoxΛ上没有零点，当且仅当存在正常数δ(与BoxΛ有关)，使得对于任意BoxI⊂Λ，当BoxI的长度小于δ时，伴随多项式f1I，…，fmI中至少一个fiI的非零系数全是正(或负)数且fi在BoxI的所有顶点上的值不为0.

2.2 存在实零点的检测

1940年，Miranda[10]证明了关于连续函数零点存在的一个定理.它的一般形式如下.

定理2(Miranda) 设BoxI=[a1，b1]×…×[an，bn]，ai＜bi.记

I-i={x∈I:xi=ai}，I+i={x∈I:xi=bi}映射f=(f1，…，fn):I→Rn是连续的.如果满足

fi(x)fi(y)＜0，∀x∈I-i，∀y∈I+i，i=1，…，n则方程f=(0，…，0)在I上有一个解.

Miranda定理在应用上有一个障碍，即条件

如何检测?

1978年Kioustelidis在文献[11]中，以及Moor和Kioustelidis在文献[12]中对连续函数使用数值方法来检测上述条件(3).但是该方法对符号计算并不合适.另外，文献[11-12]中已经指出，Miranda定理对初始的方程组可能并没有效果.需要考虑方程组

这里A是n×n的可逆矩阵.方程组g(x)=0与方程组f x()=0具有相同的零点.一个恰当的选择是令

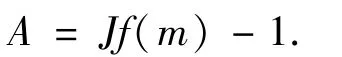
其中Jf(x)是f的Jacobian矩阵，m是BoxI的中点.

定义2非零多项式f，g∈ℝ[x1，…，xn].称多项式对(f，g)具有相对符号性质，如果其中一个多项式的非零系数都是正数同时另一个的非零系数都是负数.

对代数系统，结合伴随多项式的基本性质，我们有如下推论2.

推论2给定BoxI=[a1，b1]×…×[an，bn]和实系数方形代数系统f(x)=0.Jf(x)是f的Jacobian矩阵，m是BoxI的中点.假设行列式|Jf(m)|≠0.令

如果伴随多项式对

具有相对符号性质，则代数系统f(x)=0在BoxI上至少有一个零点.

证明由伴随多项式的基本性质1，如果伴随多项式对

具有相对符号性质，则显然有

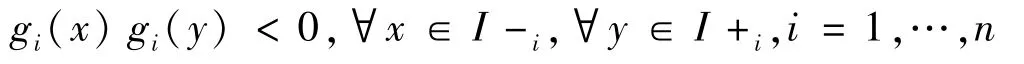
由Miranda定理，代数系统g(x)在BoxI上至少有一个零点.即代数系统f(x)=0在BoxI上至少有一个零点.

推论2比原始的Miranda定理应用方便许多，它仅仅只需要检查多项式的系数的符号就可以了.

3 算法

根据第2节的主要结果，我们能够建立如下算法

算法SAS-Zeros

输入:整系数的方形代数系统f(x)∈Z[x1，…，xn]n.

输出:正则零点的隔离Box集合.

①依次计算系统f (x)=0关于变元x1，…，，…，xn(i=1，…，n)的Dixon结式(记号x1，…，，…，xn表示去掉变元xi).获得仅含单个变元的多项式D1，…，Dn.

②令t:=2，区间长度设定为10-2，隔离D1，…，Dn的实根.获得区间集Si，i=1，…，n，并记Si中元素个数为.计算Si的直积，获得Box的集合SB

③使用伴随多项的基本性质4排除SB中不含有系统f(x)=0实零点的Box.剩余Box的集合记为SR.

④使用推论2判断SR中的Box是否含有f(x)=0的实零点.将返回"是"的Box的集合记为SY.

⑤如果SY=SB，则程序停止.如果SY≠SB，则令t:=t+1，重复以上的步骤2至5.

⑥输出:集合SY.

程序结束.

讨论算法SAS-Zeros的正确性是明显的.步骤1的计算可能失败.因为Dixon结式并不是一个完全的方法，作为替代的方法可以使用Macaulay结式，Wu方法或Groebner基方法.算法SAS-Zeros可能不终止，主要原因是重零点没有考虑.前文已指出对重零点的处理可参考文献[3].使用Maple平台，我们实现了上述算法.

4 结论

针对方形的代数系统，本文提出了一种隔离实正则零点的方法.方法主要分两大步，首先使用符号计算工具(结式或Groebner基方法均可)去获得单个变元需要满足的方程，并对单变元多项式实施实根隔离，从而得到一系列的Box.这些Box包含了原代数系统所有的实正则零点.然后利用伴随多项式方法，区分出不含零点的Box和仅仅含有一个零点Box.计算实例显示出了该方法是简洁有效的.其中的关键技术是伴随多项式方法.类似的代换方法已被应用于许多其它问题[13-14].