轨道车辆底架吊装接线箱随机振动疲劳及瞬态冲击性能研究

王剑,王兆明,李嘉明,邹庆薇

(大连交通大学 机车车辆工程学院，辽宁 大连 116028)*

轨道车辆接线箱，具有电线过渡连接的重要功能.由于轨道不平顺等原因，以吊装方式安装在轨道车辆底架位置的接线箱将会承受不同程度的振动和冲击载荷.如果在车辆运行过程中接线箱发生脱落或者振动疲劳损坏，将直接威胁行车安全.因此，在设计阶段，对接线箱的冲击强度以及随机振动疲劳性能进行分析至关重要，分析结果将作为结构设计是否合理的重要依据.BS EN 61373标准[1]目前已被广泛应用于机车车辆部件的冲击强度检验及振动疲劳寿命评估[2-3].基于频域法的随机振动疲劳寿命分析由于计算方便、仿真成本低、计算精度能够满足工程需要，在工程上应用较为广泛[4-5].瞬态动力学分析能够获得结构在惯性力和阻尼作用下的应力随时间的变化情况.验证结构冲击强度的同时，也为结构动力学特性分析提供了重要参考依据.由于结构动力学分析时，经常用经验确定阻尼比，需要对不同阻尼比下的冲击响应规律进行了研究.

本文以轨道车辆底架吊装接线箱作为研究对象，基于BS EN 61373:2010标准对接线箱进行随机振动疲劳寿命计算，验证接线箱的抗疲劳性能.基于瞬态动力学方法验证接线箱在冲击载荷作用下强度，并对比分析了不同Rayleigh阻尼系数对接线箱冲击特性的影响.

1 相关原理

1.1 随机振动基本理论

对于一个随机过程x(t),它的自相关函数定义为乘积x(t)x(t+t)的平均值[6].

(1)

式中，τ是时间坐标的移动值,T为振动的周期.

平稳随机过程中对自相关函数Фxx进行傅里叶变换，得到随机过程x(t)的功率谱密度函数:

(2)

式中,ω为圆频率.

功率谱密度函数定义了功率如何随频率分布.

而谱矩则描述随机过程谱密度的数字特征，平稳过程x(t)的谱矩定义为:

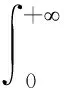
(3)

mi表示i阶谱矩.

对于一个高斯随机过程，随机应力以正斜率通过均值的平均频率为[5]:

(4)

1.2 高斯分布三区间法

对于随机振动疲劳破坏的计算，通常采用Steinberg提出的应力服从Gaussian分布的三区间法.Steinberg将应力分布分为三个区间，分别为-1σ～1σ、-2σ～2σ、-3σ～3σ，这三个区间发生振动的时间符合高斯分布，分别为总时间的68.30%、27.10%、4.33%.

结合Miner疲劳累计损伤理论，结构的疲劳损伤计算公式为：

(5)

式中：N1σ、N2σ和N3σ分别为至疲劳破坏的循环次数；N1σ为1σ区间的实际循环次数，N2σ为2σ区间的实际循环次数，N3σ为3σ区间的实际循环次数.其中：

n1σ=0.683vT

n2σ=0.271vT

n3σ=0.0433vT

(6)

式中,v为平均频率，T为试验时间.

1.3 瞬态动力学求解原理

瞬态动力学分析方法是用于计算结构对随时间变化载荷动力学响应的技术.对于某些特定结构，采用瞬态动力学方法来分析，能更好地分析惯性力和阻尼对结构振动特性的影响.

瞬态动力学分析基本方程为：

(7)

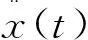
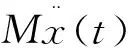
1.4 Rayleigh阻尼模型

结构的Rayleigh阻尼为刚度矩阵[K]和质量矩阵[M]的线性组合，即:

[C]=α[M]+β[K]

(8)

α和β分别为质量阻尼系数和刚度阻尼系数.

阻尼系数可以通过振型阻尼比ξi计算得到，ξi是某个振型i的实际阻尼和临界阻尼的比值.

根据Rayleigh阻尼公式，阻尼系数可用式(9)和式 (10)计算：

(9)

(10)

式中：f1和f2为任意两阶模态频率.

工程上f1～f2应该涵盖关心的频率范围.

2 接线箱模型

接线箱材质为5083.H111铝合金，接线箱通过螺栓固定在轨道车辆底架下面，如图1.一位左侧接线箱，箱体机械结构理论重量为4.848 kg，箱盖理论重量为0.985 kg，内部安装端子排重量为0.5kg，标准件共0.541 kg，箱体内部线缆共2.89kg，总计9.764 kg.一位右侧端部接线箱箱体机械结构理论重量为5.311 kg，箱盖理论重量为1.098 kg，内部安装端子排重量为1.52 kg，标准件共0.641 kg，箱体内线缆共约3 kg.穿线管及相关固定法兰共重2.534 kg，穿线管内部电缆为4.4 kg.

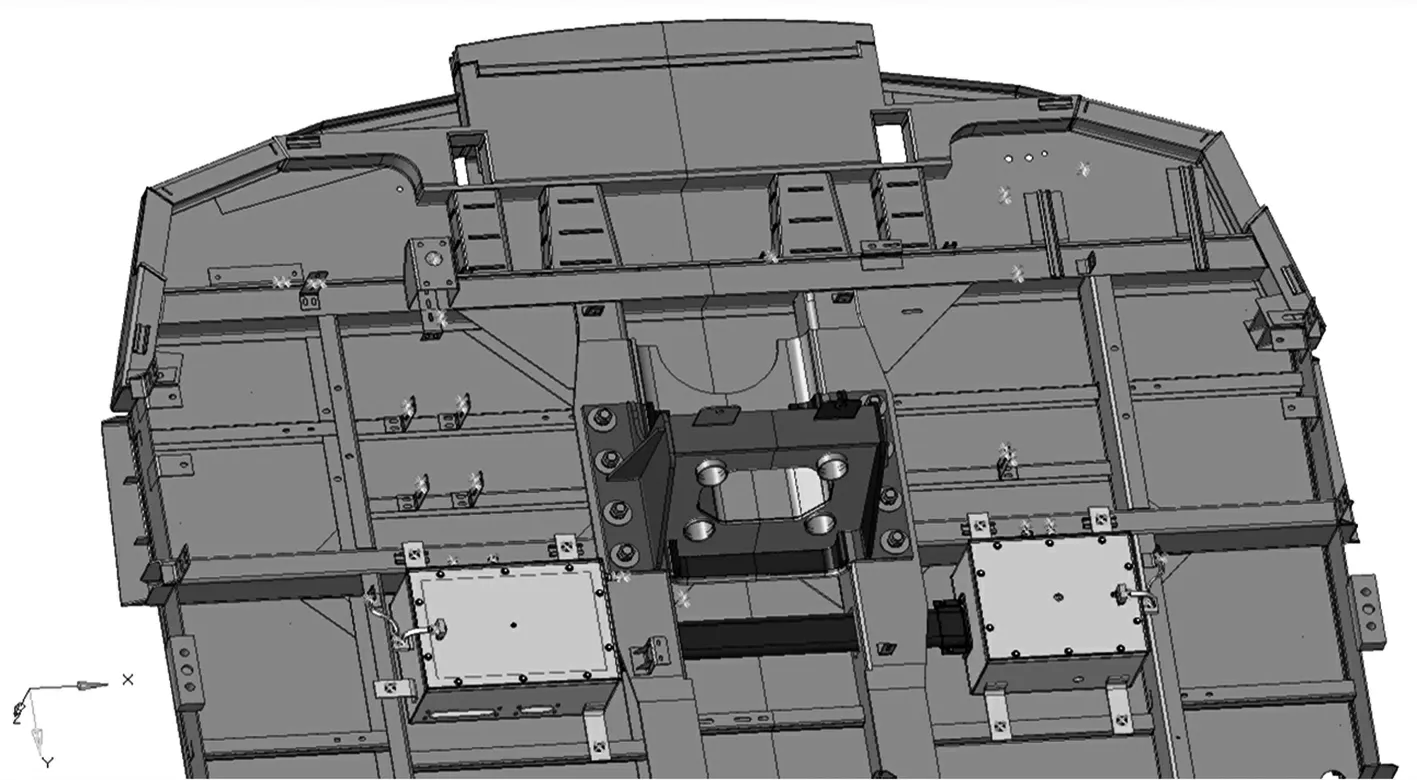
图1 接线箱在轨道车辆一位端底架布置图

规定车体横向为接线箱y向，列车行进方向为接线箱x向，垂直轨面的方向为接线箱z向.采用壳单元对接线箱模型进行离散，采用梁单元模拟>螺栓连接，接线箱有限元模型见图2.

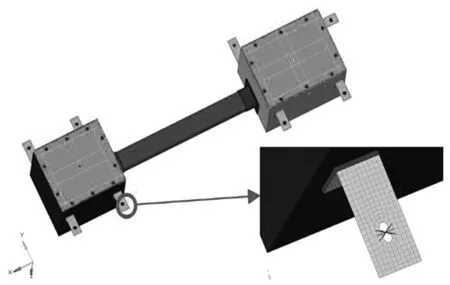
图2 接线箱有限元模型

3 接线箱随机振动疲劳分析

根据BS EN 61373:2010标准规定，接线箱随机振动疲劳寿命分析分为纵向(x向)、横向(y向)和垂向(z向)激励工况，接线箱质量小于500kg，同时接线箱直接受到车辆底架激励，因此选用1类A级的加速度功率谱，三个方向激励时，输入的ASD谱见图3.随机振动计算结果利用高斯分布三区间法，同时结合文献[7]提供的S-N曲线进行疲劳性能分析.

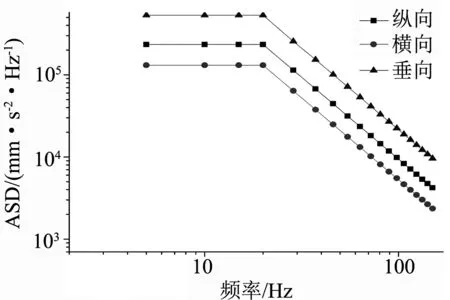
图3 接线箱施加的加速度功率谱

随机振动分析是基于模态分析结果的，因此为了进行接线箱结构的随机振动分析必须先进行有约束模态计算.

3.1 模态计算结果

本文计算模态频率范围至225 Hz，并进行振型扩展，以保证随机振动计算精度.接线箱前10阶固有频率如表1所示.其中一阶模态振型云图如图4所示.

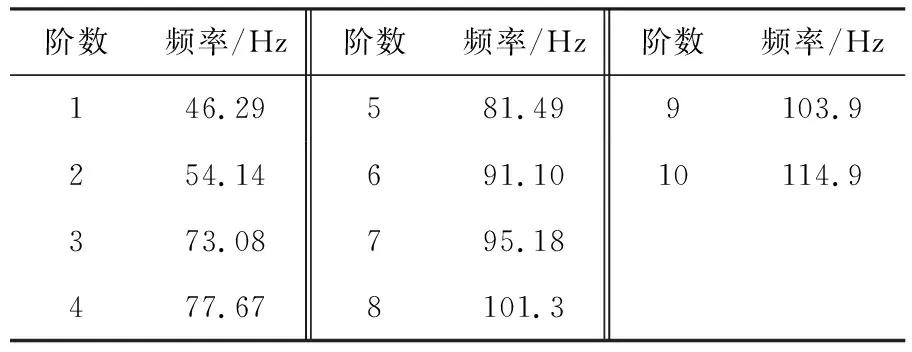
表1 接线箱前十阶模态频率

图4 接线箱一阶模态振型云图(端子排安装槽局部振动)

3.2 随机振动疲劳寿命计算

接线箱随机振动计算时，与底架连接的螺栓孔处施加六个自由度约束与ASD谱激励.

本文选取垂向激励时，接线箱等效应力1σ标准差最大位置(接线箱吊耳处)进行随机振动疲劳评估.ANSYS随机振动分析的结果值是标准差，因此采用未修匀的单元应力结果更为合适,等效应力云图如图5所示.通过应力PSD响应计算得到，接线箱在垂向随机振动载荷作用下吊耳最大应力处应力功率谱密度如图6所示，对功率谱密度曲线下方面积贡献较大的频率范围集中在一阶模态频率(46.29 Hz)和二阶模态频率(54.14Hz)附近，因此最大应力位置等效应力响应主要受一阶模态频率和二阶模态频率影响.

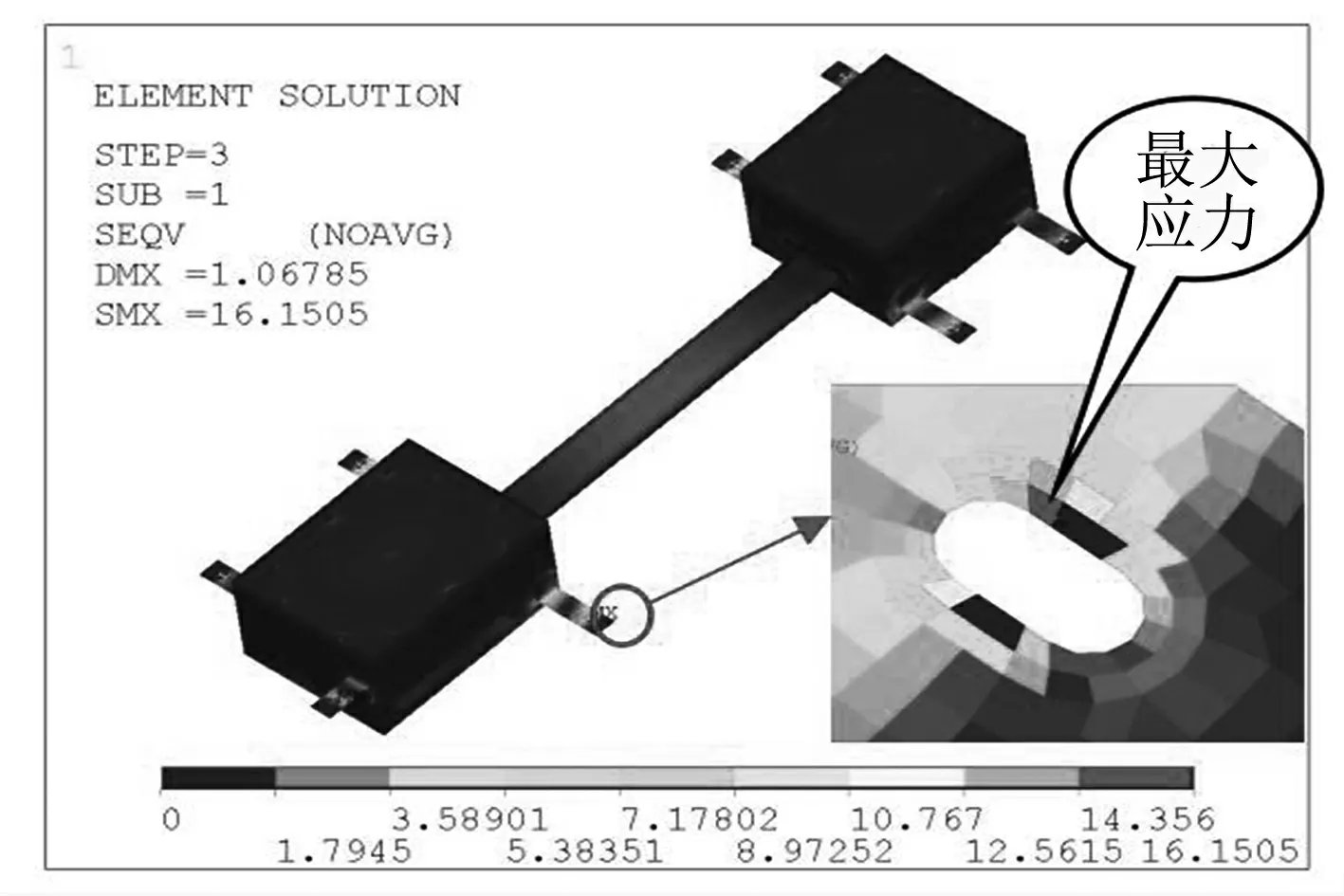
图5 垂向激励时接线箱等效应力标准差云图

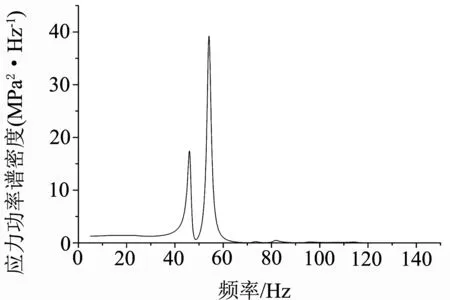
图6 吊耳最大应力处应力响应功率谱密度

结合5083铝合金母材S-N曲线[7]分别可得到1σ区间、 2σ区间、3σ区间相应应力幅下吊耳处螺孔位置至疲劳破坏的循环次数N1σ、N2σ和N3σ.纵向、横向和垂向的循环次数见表2.

表2 吊耳处螺孔位置疲劳循环次数和损伤比

根据BS EN 61373:2010标准长使用寿命试验时间规定，接线箱在横向、纵向、垂向每个方向试验时间T不得小于5 h即18 000 s.根据式(4)计算得到评估位置平均振动频率v=305 Hz,根据高斯三区间法计算可得：

n1σ=0.683vT=3749670

n2σ=0.271vT=1487790

n3σ=0.0433vT=237717

(11)

将表2中N1σ、N2σ和N3σ的值及式(11)计算的数值带入式(5)可分别得三个方向累积损伤比见表2.

由表2以及Miner累积损伤理论可知，接线箱疲劳总损伤为三个方向各激励五小时损伤的总和约为0，表明吊装接线箱满足随机振动疲劳寿命设计要求.

上述过程，基于BS EN 61373标准对接线箱进行频域方法的随机振动分析，研究了高斯三区间法在随机振动疲劳寿命评中的应用.

4 接线箱冲击性能研究

4.1 冲击载荷施加

由于接线箱模型规模较小，本文选用基于完整矩阵计算的完全法进行接线箱瞬态动力学冲击分析.

根据BS EN 61373:2010标准规定，接线箱冲击响应分析的计算工况分为垂向、横向和纵向冲击工况.垂向冲击加速度峰值为30 m/s2，横向冲击加速度峰值为30 m/s2，纵向冲击加速度峰为50 m/s2，脉冲宽度均为30 ms.其中垂向的冲击加速度半正弦脉冲时间历程如图7所示.

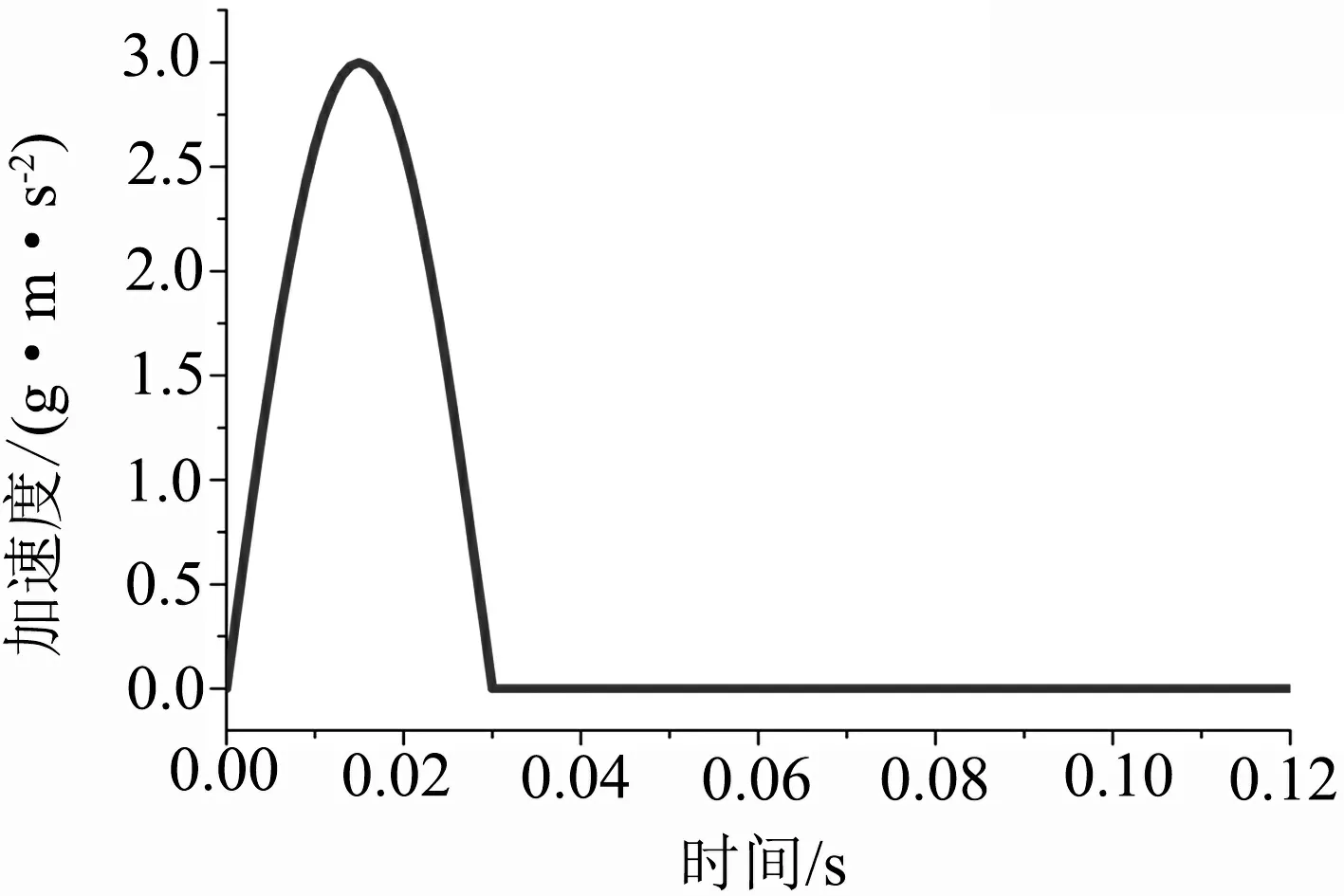
图7 接线箱垂向冲击响应分析的加速度曲线

接线箱冲击响应分析时，冲击载荷从0 s开始加载荷，脉冲宽度为30 ms，计算总时间设为0.12 s，计算时间间隔为0.001 s.

瞬态加速度冲击采用大质量法进行模拟，在接线箱和底架螺栓连接位置约束除了冲击方向的其他五个自由度.并用刚性单元把约束位置耦合在一起，主节点位置添加一个1×106t大质量单元，施加载荷函数到大质量点上，不同方向的冲击函数见式(12)和式(13).

X向通过施加整体坐标X方向载荷函数:

(12)

整体坐标系下Y、Z方向施加的载荷函数均为：

(13)

4.2 接线箱冲击计算结果

接线箱在纵向冲击时在0.015 s达到最大应力为31.35 MPa，见图8(a).横向冲击时在0.015 s达到最大应力为16.84 MPa， 见图8(b). 垂向冲击时在0.015 s达到最大应力为64.13 MPa，见图8(c)，均不会对结构产生永久破坏.

(a)纵向冲击结果

(b) 横向冲击结果

(c)垂向冲击结果图8 接线箱冲击结果(0.015 s)

4.3 Rayleigh阻尼系数对接线箱冲击特性影响

根据接线箱模态计算结果，选取一二阶模态频率作为频率范围的最小频率和最大频率，分别选取1%、2%、3%、4%、5%阻尼比，按照式(9)和(10)计算阻尼系数α和β如表3所示.

表3 不同阻尼比下的阻尼系数

以接线箱垂向冲击计算为例，分别计算不同阻尼比下接线箱冲击强度，得到等效应力-时间曲线如图9所示.

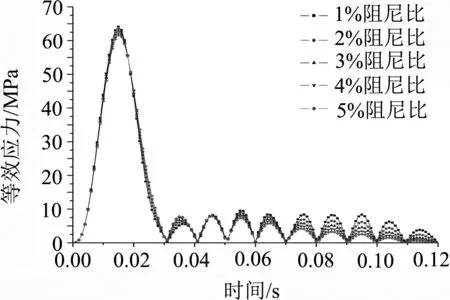
图9 不同阻尼比下评估位置应力-时间曲线

根据模态计算结果选取不同频率宽度，计算2%阻尼比时Rayleigh阻尼系数如表4所示.不同频率范围最大应力位置等效应力-时间曲线如图10所示.

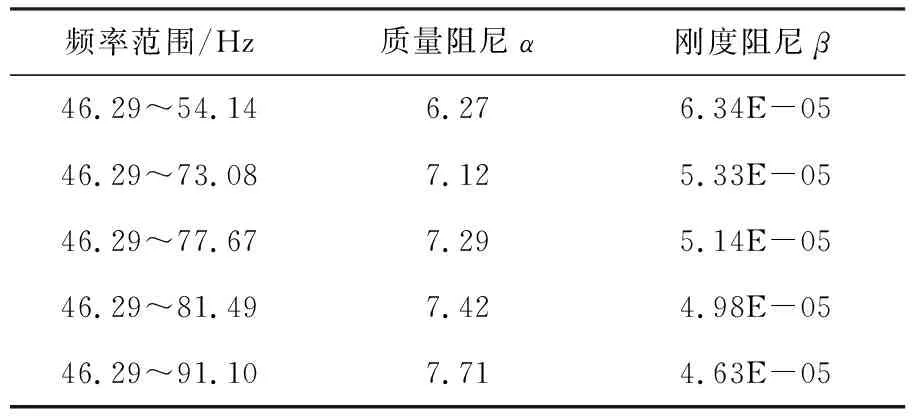
表4 阻尼比2%时不同频率范围阻尼系数

图10 不同频率范围评估位置应力-时间曲线

图9表明，不同阻尼比对接线箱最大等效应力第一个波峰应力值影响最小，随后依次增大.基于BS EN 61373标准对轨道车辆吊装接线箱冲击强度计算，等效应力峰值出现在第一个波峰，凭借经验选择阻尼比进行冲击强度计算，能够满足工程需求.图10表明，频率范围只要涵盖了关心的主要频率范围，频率范围扩大计算的Rayleigh阻尼系数对整个结构冲击特性影响极小.

5 结论

(1)对接线箱进行频域方法的随机振动分析，研究了高斯三区间法在接线箱随机振动疲劳寿命评估中的应用.计算结果为三个方向累积损伤比接近0，满足结构疲劳寿命设计要求;

(2)接线箱在经受基于BS EN 61373:2010标准规定的冲击载荷时，结构强度满足设计要求;

(3)基于Rayleigh阻尼模型验证了不同阻尼比对冲击响应第一个波峰值应力影响最小，而频率范围扩大对冲击特性影响极小.