基于节点耦合技术的螺栓强度可靠性分析

李永华，王百发，殷浩，孙琦

(大连交通大学 机车车辆工程学院，辽宁 大连 116028)*

螺栓作为起紧固连接作用的机械基础件，标准和通用程度极高，具有结构简单，拆装方便等优点.螺栓的材料属性以及工作过程中所受载荷具有随机性，螺栓失效会导致机械零部件甚至整个机械系统的功能失效，因此对螺栓强度进行可靠性分析是十分必要的.传统的螺栓强度可靠性分析基于MPC接触方法和蒙特卡罗法进行.接触分析耗时长，蒙特卡罗法抽取的样本点数量庞大，导致传统的螺栓强度可靠性分析耗时，难以实现.

惠烨等[1]基于结合面变形和构件变形的耦合关系，提出在构件间增加虚拟材料层反映结合部非线性特性的假设并建立包含结合部特性的模型，提高了螺栓和构件整体分析的准确性；李玲等[2]对螺栓与结合面因素进行综合考虑，运用功率谱函数以及WM函数表征结合面微观特征，利用Mindlin理论和统计学方法建立了能正确反映螺栓结合面刚度的分析模型；姚星宇等[3]将层单元方法应用到螺栓连接部位模拟中，给出其参数化建模方法，并证实了该方法在实际结构应用中的有效性；孙志勇等[4]基于薄层单元参数与模态参数的关系，建立响应面，并采用遗传算法实现薄层单元参数的优化辨识；Mael Couchaux等[5]基于增强束理论，建立了预测螺栓连接弹性行为的机械模型，可对螺栓力进行较为精确的评估.以上研究提高了接触区域建模的精确度，使螺栓强度分析结果更接近于工程实际，然而并未解决传统螺栓强度可靠性分析耗时严重的问题.

本文以某地铁司机室座椅连接螺栓为研究对象，建立其节点耦合模型进行强度分析，并与接触非线性分析的结果进行对比.基于节点耦合技术和响应面法对螺栓强度可靠性进行分析，该可靠性分析方法可在极大程度上节省分析时间.

1 理论基础

1.1 节点耦合技术

螺栓在实际工作的过程中，通过预紧力将多个部件连接起来.各个部件主要通过接触来传递力和力矩.可以采用在接触位置添加节点耦合的方法模拟接触行为，这种方法基于小变形理论，使部件间连接变得更加简单[6].

节点耦合就是将有接触关系的不同部件的网格节点连接，使连接的网格节点在指定坐标方向上的位移取相同数值.

根据节点耦合技术需要建立不同节点间的耦合自由度集，该集合包含一个主自由度和一个或多个其他自由度，在计算时只将主自由度在分析的矩阵方程里进行保存，而将耦合集内的其他自由度删除.计算的主自由度值将分配到耦合集内的所有其他自由度中[7-8].

一般情况下，对两个不同节点的所有自由度进行耦合，所需创建的约束方程为

UX(i)-UX(j)+0.1ROTZ(j)=0

UY(i)-UY(j)+0.1ROTZ(j)=0

ROTZ(i)-ROTZ(j)=0

(1)

当对多个节点的自由度进行耦合时，约束方程的通用关系式为

(2)

式中，i为节点的下标号，Ci为自由度系数，ui为节点自由度，C0为常数项.

1.2 响应面法

响应面法就是用一系列基函数来近似隐式极限状态函数[9-10].多项式响应面基本思想为，通过确定性试验得到一系列输入和输出值，采用最小二乘法拟合多项式函数来近似设计变量和响应值之间的映象关系.

二阶响应面(不包含交叉项)的基本形式为

(3)

式中，α0、αi、αii均为待求系数.

写成向量的形式为

X×α=Y

(4)

把样本点的值代入式(5)，利用最小二乘法得到系数向量

(5)

1.3 结构可靠性

在实际使用过程中，由于螺栓本身的材料属性及受载的不确定性，导致其工作强度会发生一定波动，当螺栓的工作强度超过其材料的屈服强度时，就会发生断裂，无法完成规定的连接功能；当螺栓的工作强度小于材料的屈服强度，则其处于安全状态，可以继续工作[11-12].

根据应力-强度干涉理论建立螺栓强度的极限状态函数

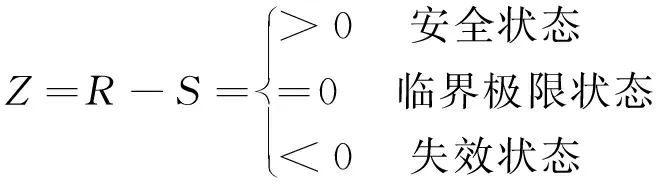
(6)

式中，R为螺栓材料的屈服强度，S为实际工况下螺栓的最大Von. Mises应力.

结构的可靠度就是Z>0的概率.

2 工程案例

2.1 节点耦合模型强度分析

为验证基于节点耦合技术和响应面法的螺栓强度可靠性分析方法可行性，以地铁司机室座椅连接螺栓为研究对象，进行螺栓强度可靠性分析.

地铁司机室座椅有限元模型如图1～2所示，主要包括头枕、靠背、座垫、座椅架和底座等结构，座椅通过螺栓与司机室地板连接.

图1 地铁司机室座椅有限元模型

图2 连接螺栓位置局部放大图

司机室座椅连接螺栓的静强度工况包括螺栓预紧力工况和紧急制动工况，其具体工况见表1.

在对接触区域进行节点耦合建模时，首先根据模型的总体受力和约束情况初步确定节点耦合区域，再根据应力和变形的分布确定耦合节点的范围，最后根据模型的传力情况确定主节点、从属节点和需要耦合的自由度.

基于节点耦合技术对接触区域进行建模，得到其有限元模型如图3所示，在螺栓预紧力工况下和紧急制动工况下分别包括13和15个耦合集.对基于节点耦合技术的有限元模型进行线性分析，所得螺栓Von. Mises应力结果如图3所示.

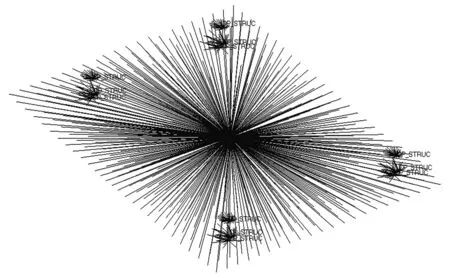
(a) 螺栓预紧力工况接触区域有限元模型

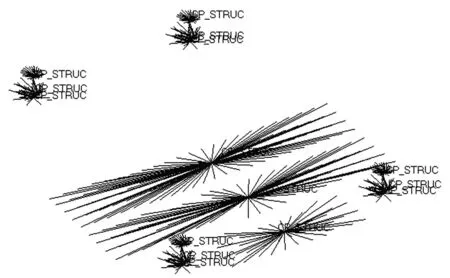
(b) 紧急制动工况接触区域有限元模型图3 基于节点耦合技术的接触区域有限元模型

由图4可知，在螺栓预紧力工况下，其最大应力出现在螺帽螺杆过渡区域，这是由于节点耦合区域过约束造成的；在紧急制动工况下，螺栓最大应力出现位置为螺杆与地板的连接位置，其分析结果符合工程实际.两个工况下的螺栓最大Von. Mises应力值为243.63 和538.12 MPa，小于螺栓材料的屈服强度640 MPa，满足强度要求.

(a) 螺栓预紧力工况螺栓Von.Mises应力云图

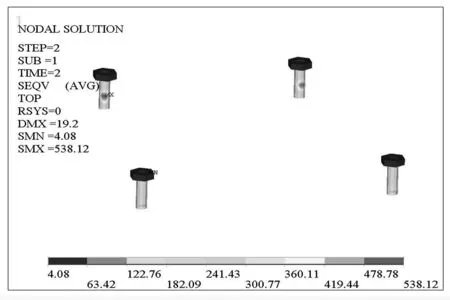
(b) 紧急制动工况螺栓Von.Mises应力云图图4 节点耦合模型的螺栓Von. Mises应力云图

2.2 接触模型强度分析

对地铁司机室座椅连接螺栓进行基于MPC接触算法的非线性分析，并将强度分析结果与节点耦合模型的强度分析结果进行对比，验证节点耦合模型强度分析结果的正确性.

进行螺栓强度的接触非线性分析前，为保证强度分析结果的准确性，需要对接触计算参数进行合理的赋值.按照工程实际经验，法向惩罚刚度(Normal Penalty Stiffness)和穿透容差(Penetration Tolerance)取0.5，摩擦系数(Friction Coefficient)取0.15，同时打开大变形开关.为加快迭代收敛速度选用牛顿-拉普森迭代法(Full Newton-Raphson).

根据表1中的静强度工况，对座椅连接螺栓进行接触非线性分析，得到螺栓预紧力工况和紧急制动工况下的迭代曲线和螺栓Von. Mises应力结果如图5 ～ 6所示.

由图5可知，在螺栓预紧力工况下，非线分析迭代到第4步时， 力F，位移U以及转矩M的范数均低于收敛准则，迭代到第11步时计算结束；在紧急制动工况下分析迭代到第13步时，力F，位移U以及转矩M的范数均低于收敛准则，迭代到第19步计算结束.两个工况的非线性分析迭代次数较少，说明分析的非线性程度较低，证明可以考虑采用线性节点耦合技术进行接触区域建模.

(a) 螺栓预紧力工况迭代曲线图

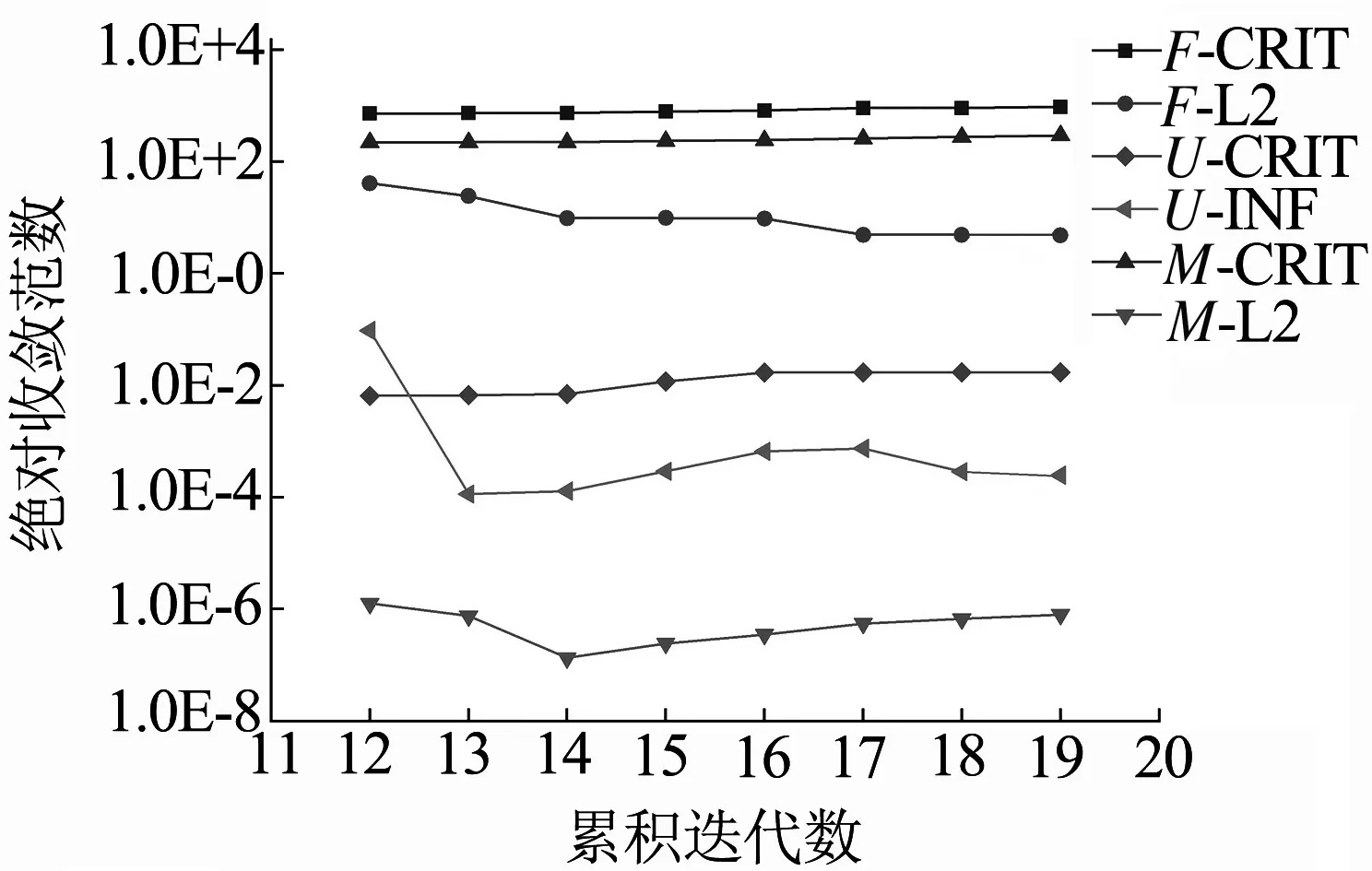
(b) 紧急制动工况迭代曲线图图5 非线性分析迭代曲线图

由图6可知，在螺栓预紧力工况和紧急制动工况下，螺栓最大应力均出现在螺杆与地板连接位置，说明在螺栓工作过程中螺杆受力较大.螺栓应力值较大的位置存在形状突变，属于应力集中高发区，说明分析结果符合工程实际.两个工况下螺栓最大Von.Mises应力值分别为249.34 和562.55 MPa，小于螺栓材料的屈服强度640 MPa.两种建模方式和工况下的螺栓最大Von.Mises应力值对比见表2.

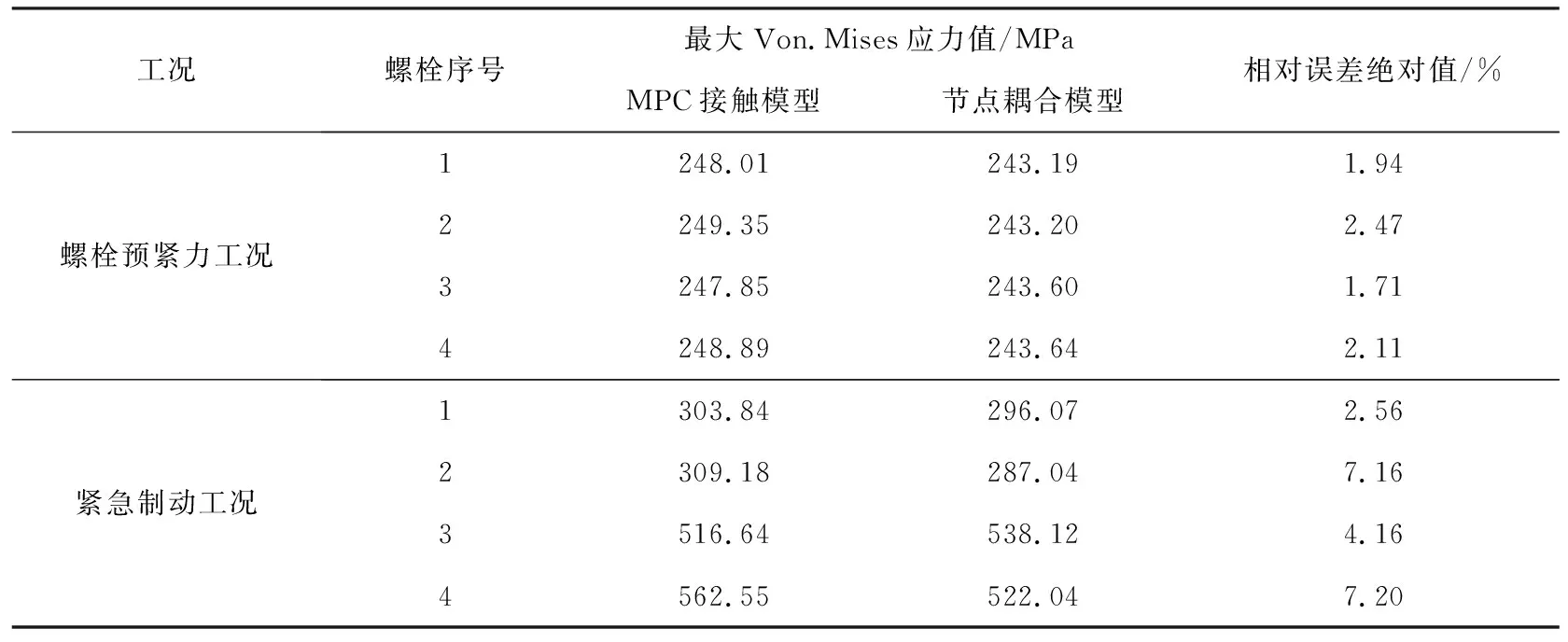
表2 螺栓最大Von.Mises应力值对比

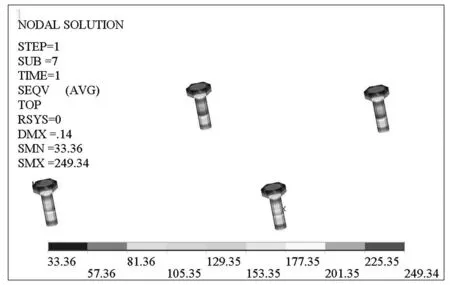
(a)螺栓预紧力工况螺栓Von.Mises应力云图

(b)紧急制动工况螺栓Von.Mises应力云图图6 接触模型的螺栓Von.Mises应力云图

由表2可知，在螺栓预紧力工况下，两种建模方式下分析所得螺栓最大Von.Mises应力值结果最大相对误差绝对值为2.47%；在紧急制动工况下，两种建模方式下分析所得螺栓最大Von.Mises应力值相对误差绝对值最大值为7.20%，保持在10%以内，证明在满足一定的计算精度要求的前提下，可以使用节点耦合技术进行接触区域建模并进行强度分析.

对两种建模方法下的分析时间进行记录，发现基于节点耦合技术的线性分析时间仅为接触非线性分析时间的4.89%.

2.3 螺栓强度可靠性分析

上文已经证明在保证一定计算精度的前提下，可以使用节点耦合技术对接触区域进行建模，且可以减少大量强度分析时间.为进一步节省可靠性分析所耗时间，在节点耦合技术进行建模的基础上，采用响应面法代替传统的蒙特卡罗法进行螺栓强度可靠性分析.

将司机室座椅两种材料的弹性模量、泊松比、螺栓预紧力以及工作外载作为设计参数，对有限元模型进行参数化，各设计参数以及分布类型见表3.

表3 设计参数及分布类型

运用中心复合设计选取初始样本点，并将其带入有限元模型中进行确定性分析，得到对应的螺栓最大Von.Mises应力值，试验设计所得部分样本点及响应值见表4.

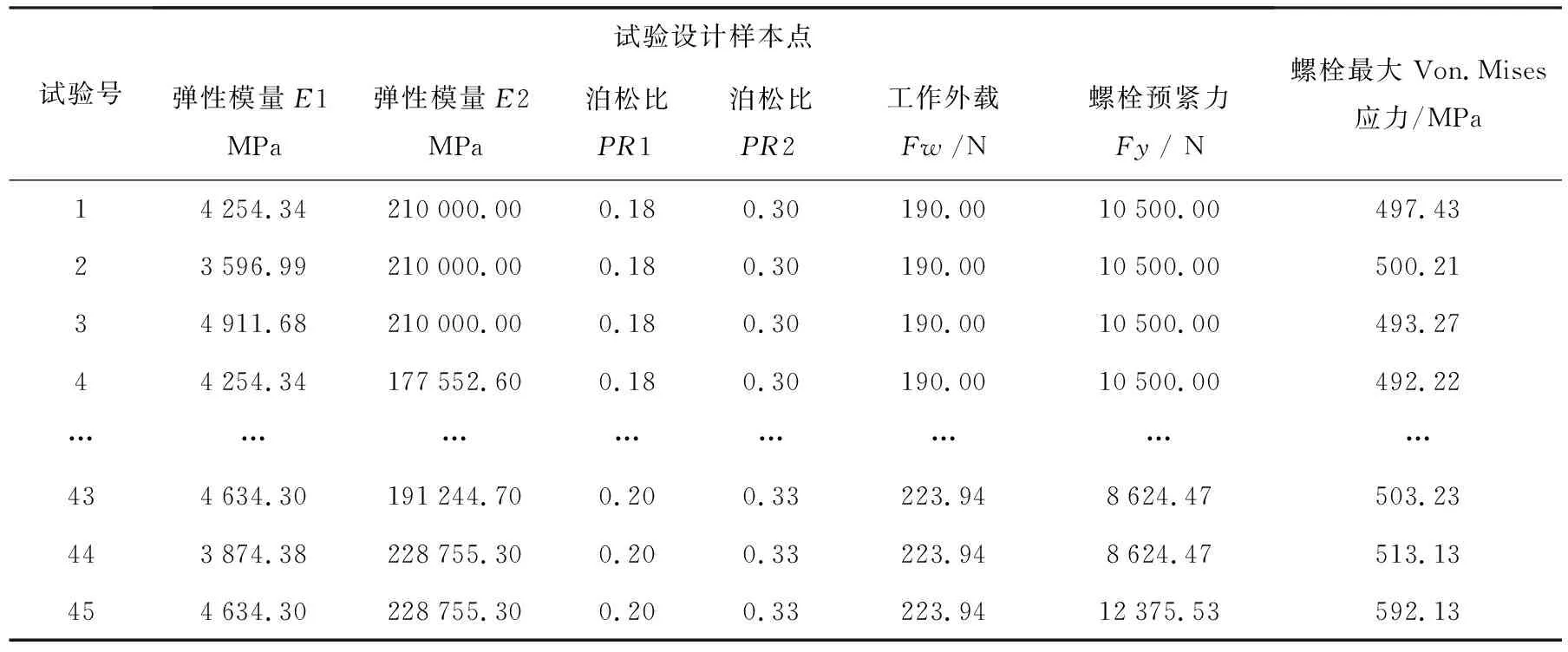
表4 试验设计及响应值

根据表4的45组样本点数据，利用最小二乘法拟合二次项系数，建立螺栓强度的多项式响应面函数为

(7)

式中，x1、x2、x3、x4、x5以及x6分别对应弹性模量E1、弹性模量E2、泊松比PR1、泊松比PR2、工作外载Fw以及螺栓预紧力Fy.

各设计参数对螺栓最大Von.Mises应力值的三维响应曲面如图7所示.

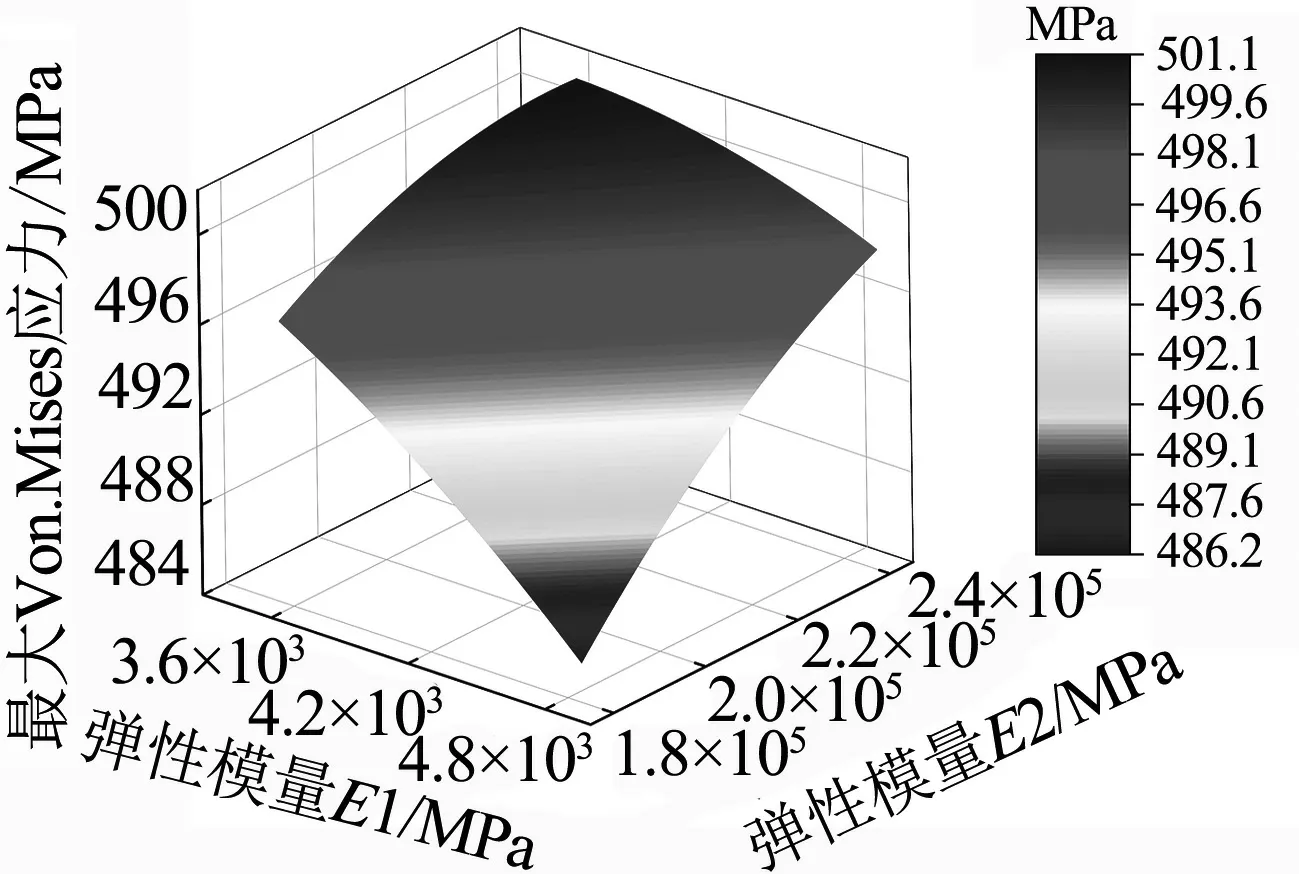
(a)弹性模量E1、E2的响应曲面

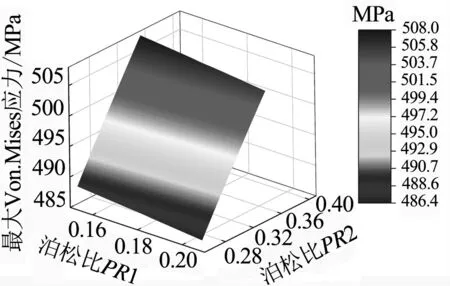
(b)泊松比PR1、PR2的响应曲面

(c)载荷Fw、Fy的响应曲面图7 设计参数对螺栓最大Von.Mises应力值的响应曲面

由图7可知，各设计参数的变化对螺栓最大Von.Mises应力值均具有一定影响，弹性模量E1和泊松比PR1的增加会导致螺栓最大Von.Mises应力值的减小，工作外载Fw、螺栓预紧力Fy、弹性模量E2和泊松比PR2的增加会导致螺栓最大Von.Mises应力值的增大，符合工程实际中的情况.工作外载Fw以及螺栓预紧力Fy对螺栓最大Von.Mises应力值的敏感性较强.

运用拉丁超立方抽样技术进行100 000次抽样，进行可靠度计算，得到极限状态函数Z的概率密度以及各设计参数对螺栓强度可靠性的灵敏度水平分别如图8 ～9所示.

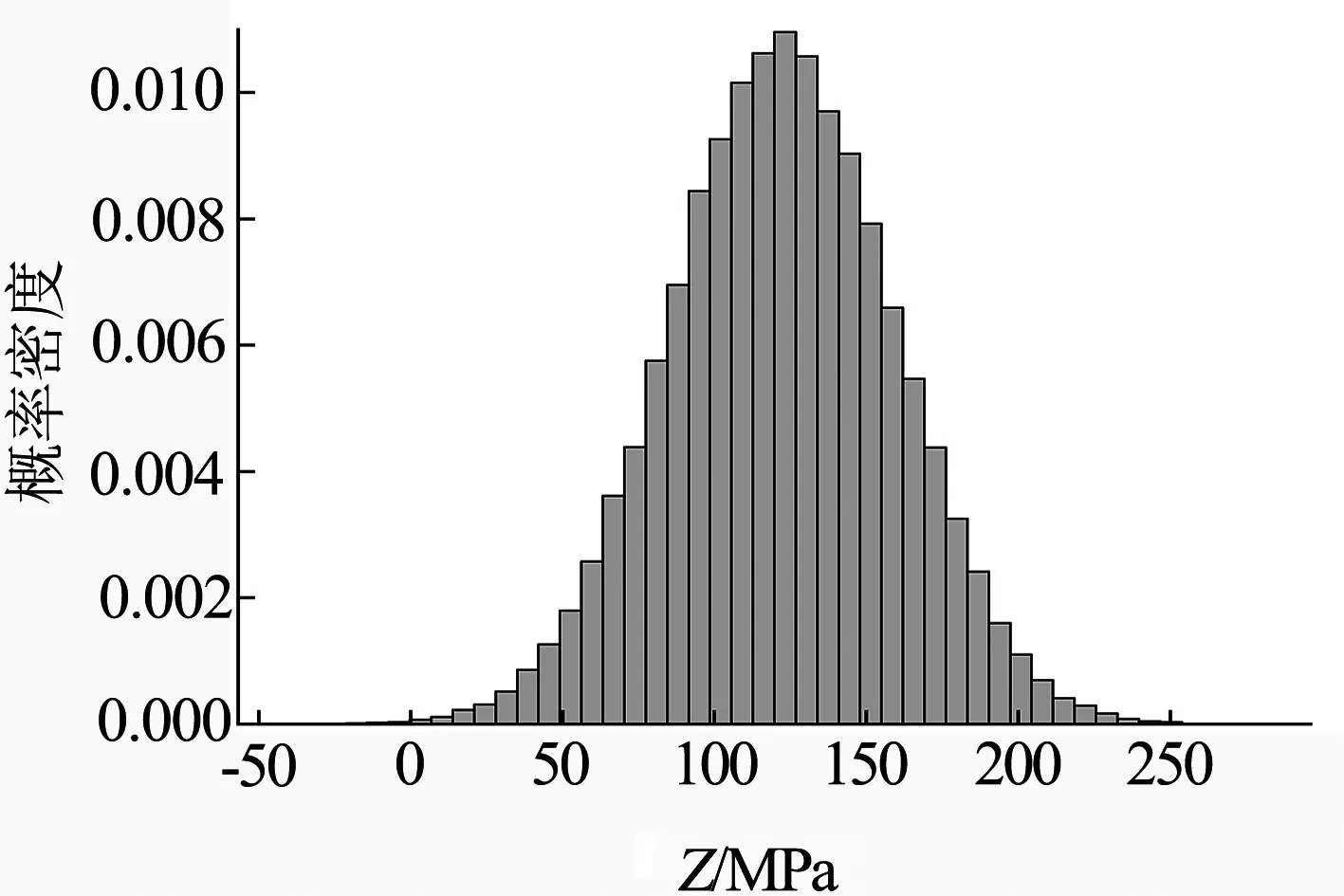
图8 极限状态函数Z的概率密度

图9 各设计参数对极限状态函数Z的灵敏度水平

由图8可知，极限状态函数Z的抽样结果接近正态分布曲线，样本点落在50 ～200 MPa之间的数量较多.提取可靠性分析结果可得到极限状态函数Z大于0的可靠度为0.999 6，即螺栓最大Von.Mises应力小于材料屈服强度，结构不会发生失效的概率为99.96 %.

由图9可知各设计参数对极限状态函数Z的影响程度.对螺栓强度可靠性影响较大的设计参数为工作外载Fw和螺栓预紧力Fy，且与工作外载和螺栓预紧力成负相关，即螺栓强度可靠性随着工作外载和螺栓预紧力的增大而减小，与工程实际情况相符.弹性模量E1、弹性模量E2，泊松比PR1以及泊松比PR2对螺栓强度可靠性的影响相对较小，可以忽略不计.螺栓强度可靠性主要受到工作外载和螺栓预紧力的影响，工作外载受现场实况的影响较大，不可控程度高，而螺栓预紧力属于人工施加，可控程度高，所以可以通过提升螺栓预紧力施加的精确度来保证螺栓强度具有较高的可靠性.

3 结论

(1)基于节点耦合技术对地铁司机室座椅连接螺栓建模并进行强度分析，解决了基于MPC接触方法的螺栓强度分析耗时问题;

(2)提出了一种基于节点耦合技术和响应面法的螺栓强度可靠性分析方法，该方法可以在极大程度上节省可靠性分析时间;

(3)可靠性分析结果显示螺栓结构不会发生失效的概率为99.96 %.由灵敏度结果可知，对螺栓强度可靠性影响最大的设计参数为工作外载Fw和螺栓预紧力Fy.在实际工程中可以通过提高螺栓预紧力施加的精确度来保证螺栓强度具有较高的可靠性.