函数凸性条件“弱化”的可能性探索

◎张逸辉 潘霄 徐莲花 王利梅 (.对外经济贸易大学，北京 0009;.中国航天系统科学与工程研究院，北京 00048)

《数学分析》教材(文献[2])给出了凸函数的如下代数定义:

定义1 设f为定义在区间I上的函数，若对I上任意两点x1,x2和任意实数λ∈(0，1)总有

f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2), (*)

则称f为I上的凸函数；反之，如果总有

f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2)，

则称f为I上的凹函数.

若将上述两个不等式改为严格不等式，则相应的函数分别称为严格凸函数和严格凹函数.

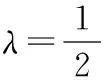
则y=f(x)是否仍为I上的凸函数.

不妨称满足不等式(**)的函数为中值凸函数.定义在开(闭)区间上的函数，其凸性和中值凸性有以下几个等价关系.

定理1(文献[3]，P101) 设y=f(x)为区间[a,b]上的连续函数，则y=f(x)为[a,b]上的凸函数的充要条件是y=f(x)为[a,b]上的中值凸函数.

证明:根据凸函数和中值凸函数的定义，只需证明充分性.

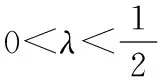
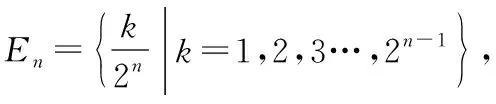
首先用数学归纳法证明：对任意正整数n，以及任意的x1,x2∈[a,b],对一切λ∈En，都有不等式(*)成立.

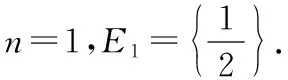
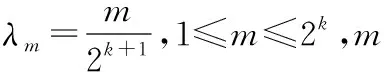
f(λmx1+(1-λm)x2)

≤λmf(x1)+(1-λm)f(x2)，

即当n=k+1时，不等式(*)对λ∈Ek+1成立.

因为f(x)在[a,b]上连续，所以对任意的x1,x2∈[a,b]，有

=λf(x1)+(1-λ)f(x2).

综上，f(x)为[a,b]上的凸函数.证毕.

定理2 区间(a,b)上的有界中值凸函数处处连续.

定理2的证明见[文献1，P288].

定理3 区间(a,b)上的可测中值凸函数处处连续.

定理3的证明见[文献4,P122].

注:由定理1、定理2和定理3可知，若f(x)为开区间(a,b)上的有界或可测函数，则f(x)为凸函数的充要条件是其为中值凸函数.

通过考察下例，我们可以看到定义在离散点集上的中值凸函数，即使有界，也不一定为凸函数.

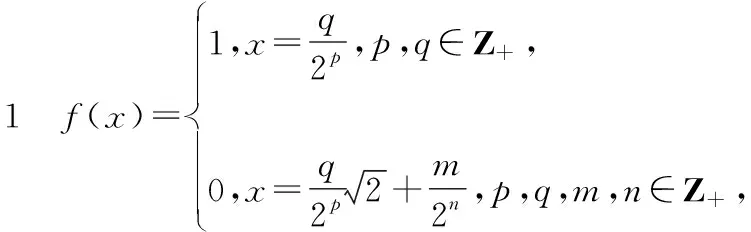
其中Z+代表正整数集.

若取x1,x2均为第一类(或第二类)的x，则显然有

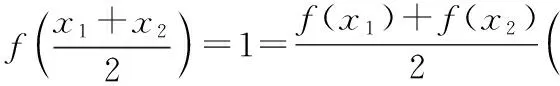
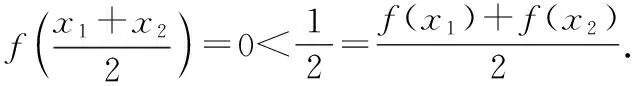
这个反例的构造，灵感源于狄利克雷函数.同样地，反例的图像也不能画出.在这里，高等数学的抽象性得以体现.