两类Beta算子的收敛阶

蔡清波,周国荣

(1.泉州师范学院数学与计算机科学学院,福建 泉州 362000；2.厦门理工学院应用数学学院,福建 厦门 361024)

1 预备知识

设f是定义在[0,1]上的可积函数,Lupas[1]提出了如下正线性积分型Beta算子：

(1)

本文在此基础上结合若干数值例子对算子(1)的收敛性质做进一步研究. 由于算子(1)仅为常数保持算子,所以提出如下线性保持的修正的Beta算子：

(2)

2 一些引理

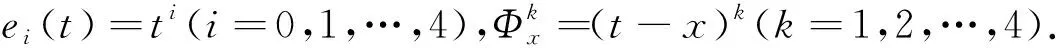
引理1令x∈(0,1)， 以下等式成立：

βn(e0;x)=1;

βn(e4;x)=

证明由式(1)及Beta函数的定义和性质, 显然有βn(e0;x)=1成立. 当i=1,2,…时,有

从而, 引理1证毕.

引理2令x∈(0,1)，以下等式成立：

(3)

(4)

(5)

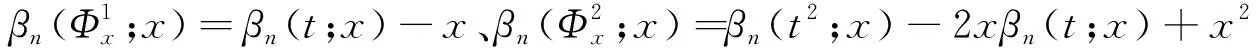
6x2βn(e2;x)-4x3βn(e1;x)+x4βn(e0;x)=

引理2证毕.

推论1令x∈(0,1)，由引理1和引理2易知以下极限式成立：

(6)

(7)

(8)

证明由式(2)、引理1和引理2经简单计算易知引理3成立.

(9)

(10)

(11)

(12)

(13)

3 收敛阶的估计

首先给出βn(f;x)的局部逼近定理.

证明构造辅助算子：

x∈(0,1).

(14)

此外,又因为

‖f‖βn(e0;x)+2‖f‖≤3‖f‖，

(15)

所以由式(14)和(15)可得

对式(15)右端的g∈C2(I)取下确界, 可得

|βn(f;x)-f(x)|≤

从而,

其中,M为正常数. 定理1证毕.

由定理1、式(2)、(9)和(10)易知以下定理成立.

定理3设f∈C(I)，对于算子βn(f;x),有

证明对于取定的x∈(0,1)，由Taylor公式,有

f(t)=f(x)+f′(x)(t-x)+

由Cauchy-Schwartz不等式,有

定理3证毕.

4 数值结果

例1令f(x)=sin(2πx)，在图1(a)中给出了f(x)和n分别取10,50，100的βn(f;x)算子的曲线像. 在图1(b)中给出了n分别取10,50,100时的逼近误差|f(x)-βn(f;x)|的曲线.

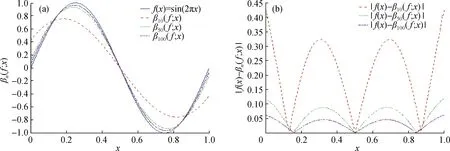
图1 βn(f;x)算子的逼近趋势(a)和逼近误差(b)Fig.1 The approach trend (a) and approximation error (b) of βn(f;x) operators

图算子的逼近趋势(a)和逼近误差(b)Fig.2 The approach trend (a) and approximation error (b) of operators

图3 βn(f;x)和的逼近趋势(a)和逼近误差(b)比较Fig.3 The comparison of approach trend (a) and approximation error (b) of βn(f;x) and operators

表1 n取不同值时βn(f;x)和的逼近误差上界Tab.1 The approximation error upper bound ofβn(f;x) and operators with different n

5 结 论

本文首先引入了一类常数保持和一类线性保持的Beta算子, 通过对这两类Beta算子的矩量和中心矩量的估计, 分别得到它们的收敛阶和Voronovskaja型渐近展开公式. 然后, 通过若干数值例子的图像给出了两类算子对不同函数的收敛效果并进行数值误差估计.