例谈运算教学中算法模型的建构策略

高峰龄 韦波富

【摘 要】数的运算，重在理解算理，形成算法。教学中可通过操作、想象、事理分析等活动来明晰算理，进而逐步抽象算法;通过猜想验证或整体归纳概括，渗透数学思想，构建算法模型。在解决实际问题过程中，教师可引导学生运用算法模型，积累活动经验，体悟数学思想。

【关键词】算理 算法 模型 数学思想

运算一直以来就是数学学习中首要的学习任务。从小学数学课程编排和教学实践看，整数、小数、分数的计算贯穿始终，运算是小学数学学习的主要内容之一。《义务教育数学课程标准（2011年版）》中提出：运算能力是指能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解算理，寻求合理简便的运算途径解决问题。运算不仅仅是要会算，形成技能，还要在运算学习过程中明晰算理、理解算法、提升思维、运用思想，要正确理解算理和对象，掌握运算法则，分析数量关系以解决问题。

现结合教学实例，谈谈运算教学中算法模型构建的策略。

一、循理入法，构建算法模型

一步运算是运算教学的基础，运算的掌握有助于算理的理解，而算理又能帮助解决实际问题。在理解算理的基础上抽象算法，需要以数学思想为指引，先构建算理与算法的联系。

【案例1】三年级上册“两位数除以一位数”的例题如图1。

1.逐层深入，理解算理

教材中提供了3种理解算理的途径，逐层抽象：

（1）实物操作。利用小棒分一分，先平均分4捆，每份2捆;再平均分6根，每份3根。这一途径通过半具体半抽象的活动，让学生理解算理，感悟算法。

（2）看图想象。从题图中观察得出，每班先分得2筒羽毛球，再分得3个羽毛球。这一途径通过建立表象活动，让学生理解算理。

（3）口算方法。先用十位数40除以2，再用个位数6除以2，最后将两个得数相加得到23。这一途径通过抽象活动，让学生理解算理。

教师引导学生在分小棒和看图分羽毛球的半具体半抽象操作过程中感知到分与合的思想，对应数学算法，深刻理解将被除数46分成40和6，先用40除以2，再用6除以2，最后将两次分得结果合并的算理，逐步上升为抽象的数学运算。同时运用数形结合，感悟分合思想，借助口算理解46÷2的算理。

三种途径清晰地分析了这一道算式的算理，学生虽然听清楚了，但还需要内化理解算理，真正学会除法计算的算理和算法。运用以上理解算理的方法途径，可以让学生自主开展理解算理的活动。

2.以理驭法，构建模型

仅仅依靠一道题的分析，就让学生联系算理、算法间的关系，构建算法模型显然不够。教学时教师可增加事例帮助学生理解算理，强化具体操作与抽象算法之间的关联，帮助学生深入理解算理和算法，构建算法模型。学生通过对题组的观察，借助已有的活动经验，丰满对算理的理解，建立算理与算法之间的联系;通过对一些事例的观察、比较，发现都是将被除数按数位分成十位数和个位数，分别除以除数，再将结果合并这一规律，在此基础上概括、归纳后，提炼算法，构建算法模型，深化数学思想的渗透运用。

用竖式形式进行运算时，学生只要结合对算理的理解，将算理与竖式计算过程一一对应，规范书写形式即可。

3.解决问题，运用模型

学生构建出两位数除以一位数的算法模型后，由此可以扩展到三位数除以一位数的算法模型构建，如639÷3，运用模型能够自主建构算理与算法的联系。对于以后学习类似45÷3、206÷5的运算，学生有了算法模型的构建方法后，可以形成探究运用模式，这就是模型思想的力量。

学生经历了理解算理、建构算法的过程，感悟到模型思想的实用性后，我们还可以把除法口算与乘法口算的过程进行横向比较，丰富算法模型，提升学生的数学思维能力。

二、猜想验证，构建算法模型

到小学高年级，学生积累了丰富的活动经验，抽象、推理能力较低年级明显提升。教学时可引导学生通过观察、比较的方法，逐层抽象算法，构建算法模型。

【案例2】六年级上册“分数乘分数”的例题。

1.寻根溯源，猜想算法

教师可从抽象的分数意义和乘法意义入手，在画图操作中引导学生得到计算结果。

（1）图2中斜线部分是涂色部分的几分之几？也就是谁的1— 4？1— 2的1— 4是整张纸的几分之几？

通过2个4是8，知道把这张纸平均分成8份。那么，1— 2的1— 4是多少你能用算式表示出来吗？同理，结合图3抽象出1— 2的3— 4的算式和结果。

（2）一台拖拉机，每小时耕地2— 3公顷，1—5 小时耕地多少公顷呢？

学生结合情境，通过画图（如图4）抽象出2— 3乘1— 5的意义，并得到结果。同时利用已有探究经验，在图5中表示出4— 5  小时耕了多少公顷，得到2— 3乘4— 5的意义和结果。

教師应引导学生回顾探究这几道算式意义和结果的过程，让学生在抽象概括活动中，形成对算法的合理猜想。

2.举例验证，构建模型

算法猜想是否合理正确，需要进行验证。通过举例，学生验证算法猜想的正确性，再联系分数乘整数的算法，形成分数乘法算法模型。

在初步理解算理的基础上，教师可引导学生合理猜想，开展“猜想——验证”数学探究活动（见表1）。经历算法模型构建的过程，有助于学生感悟、运用数学思想方法，提升思维能力。

我们的猜想 分子相乘的积作分子，分母相乘的积作分母？

我的验证 1.按照猜想算一算：

1—3  ×1— 4 =1×1—3×4  =1— 123—4  ×3— 5 =3×3—4×5  =9— 20

2.根据算式的意义画图验证：

我的结论 猜想     成立（） 不成立（）

三、以事明理，构建算法模型

混合运算重在对运算顺序的理解，教学中需要让学生明晰运算顺序是什么，为什么是这样，并能构建运算顺序模型加以运用。

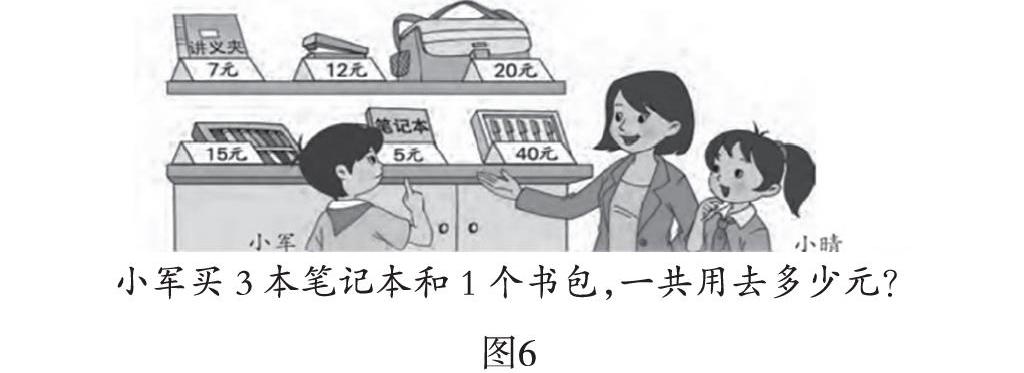
【案例3】三年级下册“不带括号的两步运算”的例题，如图6。

1.分析数量关系，理解算理

教师可引导学生借助数量关系解决实际问题，用事理明白算理。学生尝试列出综合算式5×3+20或20+5×3，通过数量关系，理解需算出3本笔记本多少元的原因，所以先算5×3。教学中教师还可以用运算的意义让学生明晰运算顺序，观察算式5+5+5+20或20+5+5+5，其中5+5+5表示3本笔记本的价钱，可以写成5×3。乘法是加法的简单写法，且比加法高级，所以先算乘法。通过不同途径让学生初步感知到运算顺序的算理。

2.归纳题组算法，构建模型

让学生在理解算理的过程中构建运算顺序模型，从中感悟运用数学思想的必要性，有利于提升思维能力。仅仅用一道混合运算能概括出有乘法和加、减法的运算顺序吗？显然不能，还需要对较多的题组素材进行观察、比较，开展抽象、归纳、概括活动，发现不同事例中运算顺序的相通之处，从而建构运算顺序模型。

3.解决实际问题，运用模型

学生建构了运算顺序模型后，还要能够会运用该模型。教师可设计解决实际问题的题组：某公园的儿童票每张4元，成人票每张8元，现一共有50元。根据已知信息，解释以下算式表示的意义：（1）8+4×5;（2）8×2+4;（3）50-4×6;（4）8×7-50。

要知道这些算式表示的意义，学生需在数量关系的支撑下运用运算顺序模型解决问题，在厘清綜合算式里每一步运算顺序的前提下，真正理解算式的意义，知道算式解决的是什么问题。

对于三步及以上混合运算的顺序教学，我们可以在分析数量关系的基础上，理解运算顺序，构建运算顺序模型。如四年级上册第七单元《整数四则混合运算》中的例2、例3（见图7）直接出示算式，利用学生对小括号的已有认知，迁移到有小括号和中括号的多步运算中，得到混合运算的顺序。这样的编排其实不利于构建算法模型，提升学生思维。

其实，教师可以为例2、例3创设情境，学生在问题解决的过程中，从分析数量关系入手，尝试列综合算式，探究运算顺序。探究过程中，学生可以对一组算式进行研究，发现运算顺序特点后构建模型;也可以采用“猜想——验证”的探究路径。不管采用哪一种学习方法，都是对已有数学思想的渗透运用，都能够有效提升学生的数学思维。

学生在学习三步计算运算顺序后还会遇到更多步数的计算，在明晰运算顺序的“理”之后，经历了“化繁为简”的过程后，可以感受到多步运算顺序的“序”，构建出运算顺序模型，感悟数学思想，并最终运用运算顺序模型解决问题。

我们要关注学生学习过程中思维的培养，让学生感悟思想方法。在“四则混合运算”的教学中，注重推理、转化思想的渗透，教给学生用联系沟通的方法学会学习，在教学中抓住数量关系在运算顺序学习中的关键作用，以事理明算理，使学生内隐的思维外显，培养思维能力。

综上，教师在运算教学中，可以引导学生集中操作，将抽象算理具象化，形成算法表象;可以让学生利用已有知识经验迁移类推，合理猜想算法，进而验证猜想;还可以指导学生通过数量关系分析，在明晰事理的基础上理解算理，形成算法。教材编排“数的运算”知识时，多采用一事一例的方法，让学生对具体事例进行探究，理解算理，抽象归纳算法。实际教学中教师也可以重组教材的例题和习题，多呈现一些事例，丰富学习探究的素材，在抽象、推理、模型数学思想的渗透运用过程中，教会学生构建算法模型。