二次矩阵方程异类约束1-3-7解的迭代算法

陈世军， 余胜斌

(阳光学院 基础教研部，福建 福州 350015)

在工程学、控制理论等领域中很多问题都可以归结为求矩阵方程约束解.近年来，诸多学者对单变量二次矩阵方程进行了许多研究，取得了丰富的成果并建立了一些有效的算法[1—4].例如，崔学莲[1]提出了二次矩阵方程X2+AX-B=O在矩阵区间[L,U]的约束解的迭代算法，并证明了该算法的收敛性；金继承[2]提出了保结构加倍算法,用于阻尼系统的二次方程的数值求解，并给出了算法的迭代格式和收敛性证明；李媛媛[4]利用固定点理论和矩阵范数的相关知识, 给出了二次矩阵方程X2+2AX+B=O有解的充要条件和有唯一解的判定定理.共轭梯度算法是求矩阵方程约束解的有效算法之一.近几十年来，很多学者研究了基于共轭梯度算法的矩阵方程(组)的约束解.对于非线性矩阵方程求解，牛顿算法和共轭梯度算法是一种有效的算法[5—17].孙颖异[5]通过修正共轭梯度参数，构造新的搜索方向, 提出两类修正的WYL共轭梯度法，证明了算法的全局收敛性； J.H.Long[6]等建立了求解二次矩阵方程的改进牛顿算法，且给出了算法的收敛性证明；张凯院[10]建立了双矩阵变量Riccati矩阵方程AX1B+CX2D+X1E1X2+X2E2X1=E3对称解的牛顿-MCG算法.对于多变量二次矩阵方程异类约束解，目前还没有得到研究，因此本文基于牛顿算法和修正共轭梯度算法，建立了求多变量二次矩阵方程的异类约束解，这里的约束解是指对称解、中心对称解和自反解.

本文研究三变量二次矩阵方程的异类约束解，矩阵方程形式如下：

M1X1N1+M2X2N2+M3X3N3+

X1H1X2+X2H2X3+X1H3X3+Q=O.

(1)

1 求矩阵方程(1)异类约束解的牛顿算法

定义1划分n阶单位矩阵I=(e1,e2,…,en)，称S=(en,en-1,…,e1)为n阶次单位矩阵．若矩阵X∈Rn×n满足SXS=X，则称X为中心对称矩阵.

定义2设P∈Rn×n满足PT=P，P2=I，若X∈Rn×n满足PXP=X，则称X为关于矩阵P的自反矩阵.

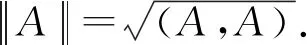
为了使表达式更简洁，引进以下矩阵记号：

对矩阵函数ψ(X+tY)在t=0处求导，得

M1Y1N1+M2Y2N2+M3Y3N3+

X1H1Y2+Y1H1X2+X2H2Y3+

Y2H2X3+X1H3Y3+Y1H3X3.

记

φX(Y)=φX(Y1,Y2,Y3)=

M1Y1N1+M2Y2N2+M3Y3N3+

X1H1Y2+Y1H1X2+X2H2Y3+

Y2H2X3+X1H3Y3+Y1H3X3.

γ(Y)=Y1H1Y2+Y2H2Y3+Y1H3Y3.

因此可得

ψ(X+Y)=ψ(X1+Y1,X2+Y2,X3+Y3)=

ψ(X)+φX(Y)+γ(Y)，

(2)

其中φX(Y)是指矩阵函数ψ(X)在“点X”处沿着“方向Y”的Frechet导数.

不妨假设(X1,X2,X3)∈Ω1-3-7是二次矩阵方程(1)的一组近似解，则求二次矩阵方程(1)的一组解(X1,X2,X3)等同于求一组校正值(Y1,Y2,Y3)∈Ω1-3-7使之满足方程ψ(X+Y)=O，当(Y1,Y2,Y3)谱半径均小于1时，由牛顿算法原理可以忽略矩阵(Y1,Y2,Y3)的高次项γ(Y)，因而方程(2)可以近似为ψ(X+Y)≈ψ(X)+φX(Y).因此求解ψ(X+Y)=O可转化为求(Y1,Y2,Y3)∈Ω1-3-7使之满足线性矩阵方程

φX(Y)=-ψ(X).

(3)

结合牛顿算法原理，建立求矩阵方程(1)异类约束1-3-7解的牛顿算法：

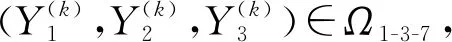
φX(k)(Y(k))=-ψ(X(k)).

Step 3 计算X(k+1)=X(k)+Y(k)，令k∶=k+1，转到Step 2.

牛顿算法中有收敛性结论：假设矩阵X*是二次矩阵方程(1)的一个单根，并且初始矩阵X(1)能充分接近X*，则牛顿算法迭代所得矩阵序列{X(k)}能二次收敛于X*.

2 问题的提出

记A1=M1,B1=N1,C1=M2,D1=N2,E1=M3,F1=N3，A2=I,B2=H1X2,C2=X1H1,D2=I,E2=X2H2,F2=I，A3=I,B3=H3X3,C3=I,D3=H2X3,E3=X1H3,F3=I,G=-ψ(X).建立求线性矩阵方程(3)异类约束解的MCG算法，给出方程(3)的一般形式：

(4)

其中Ai,Bi,Ci,Di,Ei,Fi,G∈Rn×n(i=1,2,3).主要讨论下面2个问题：

问题1假设关于Y1,Y2,Y3的方程(4)有解，则求(Y1,Y2,Y3)∈Ω1-3-7，使方程(4)成立.

问题2假如方程(4)无异类约束1-3-7解，则求(Y1,Y2,Y3)∈Ω1-3-7，使得

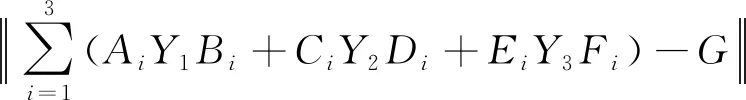
3 求解问题1的MCG算法

基于共轭梯度算法的基本思路，结合方程(4)中矩阵特点，修改有关矩阵的类型，建立求解问题1的MCG算法.先引入记号：

算法1 (问题1的MCG算法)

Step 2 若Rk=O，或者Rk≠O且Qk=O，则停止计算；否则，继续计算

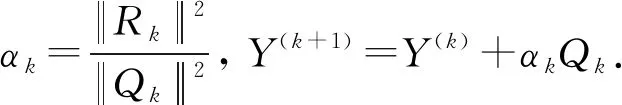
Step 3 计算

Rk+1=G-μ(Y(k+1))，

Qk+1=

Step 4 令k∶=k+1，转Step 2计算.

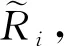
性质2若k≥2，则算法1中得到的矩阵Ri和Qj满足

i≠j；i,j=1,2,…,k.

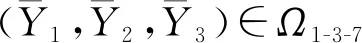
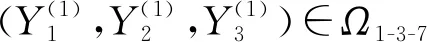
4 求解问题2的MCG算法

由定理1可知当Rk≠O而Qk=O时算法1中断，即方程(4)无异类约束1-3-7解.因此，需要求方程(4)的最小二乘异类约束解，即求矩阵(Y1,Y2,Y3)∈Ω1-3-7使得

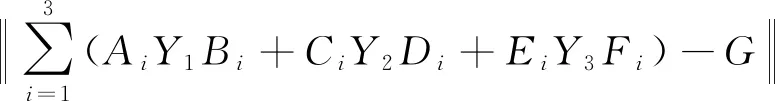
下面通过将矩阵方程组按行拉直，构造方程(4)的等价正规矩阵方程，将求解问题2转化为求解等价矩阵方程异类约束1-3-7解的问题.然后参照算法1，建立求解问题2的MCG算法.

引进记号：

u(Y1,Y2,Y3)=

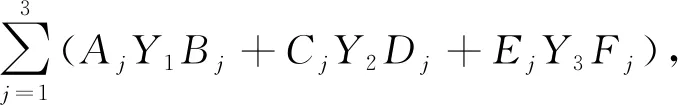
v(Y1,Y2,Y3)=

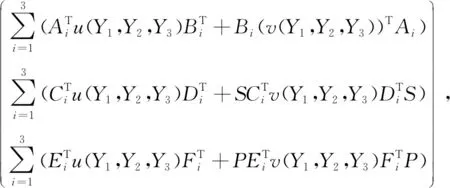
M=

定理2求解问题2等价于求约束正规矩阵方程f(Y)=K的异类约束1-3-7解，且该正规矩阵方程一定有异类约束1-3-7解.

证明求解问题2等价于求(Y1,Y2,Y3)∈Ω1-3-7，使得

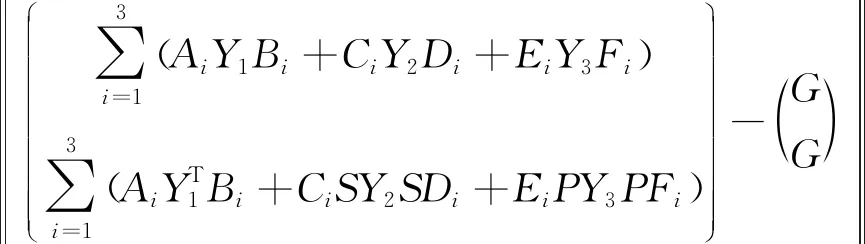
(5)

下面证明求解极小值问题(5)等价于求矩阵方程f(Y)=K的异类约束解.将矩阵方程组

(6)

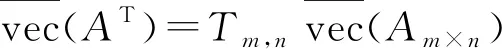
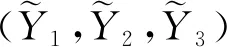
参照算法1以及MCG算法原理，建立求矩阵方程f(Y)=K异类约束解，即求解问题2的MCG算法如下：

算法2(问题2的MCG算法)

Step 2 若Rk=O，则停止算法2计算；否则，继续计算

Step 3 计算

Step 4 令k∶=k+1，转Step 2.

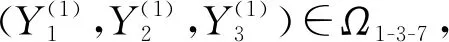
5 数值算例

下面给出算例1，在算例1中通过改变矩阵的阶数，说明文中建立的MCG算法1和MCG算法2是可行的，具有很高的效率，且能求出矩阵方程(1)异类约束1-3-7解或异类约束最小二乘解.这里计算时间(s)、系数矩阵的阶数、MCG算法1、MCG算法2、MCG算法1中断次数、实际误差的F-范数分别用time、n、k1、k2、k12和error表示.结合牛顿算法以及MCG算法1、MCG算法2，采用如下步骤计算：

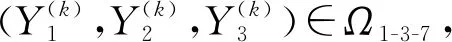
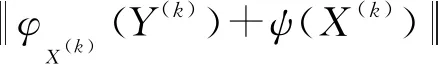
Step 3 计算X(k+1)=X(k)+Y(k)，置k∶=k+1，转Step 2.

例1用文中建立的牛顿-MCG双迭代算法求矩阵方程(1)的一组异类约束1-3-7解和最小二乘解，方程(1)系数矩阵均为n阶方阵，系数矩阵、终止准则ε如下：

Mi=Ni=Hi=I(i=1,2,3)，

选取初始矩阵X1=1.3I,X2=0.94I,X3=1.05I，Y1=Y2=Y3=O，按计算步骤求得矩阵方程(1)的异类约束1-3-7解.结果见表1(MATLAB软件2014版-PIV3.0 GHZ微机).

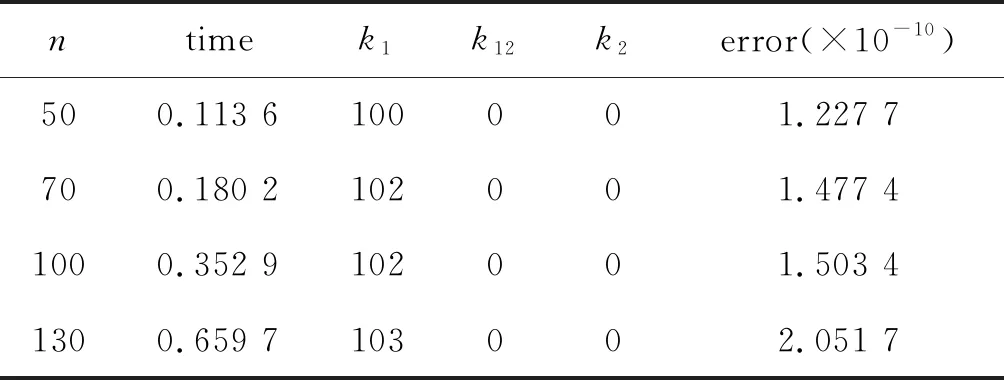
表1 方程(1)的异类约束解计算结果

当n=5时，可得矩阵方程(1)的异类约束1-3-7解为

若选取初始矩阵为X1=2I,X2=0.2I,X3=3I，Y1=Y2=Y3=O，n=5，按计算步骤得到矩阵方程(1)的异类约束1-3-7解为

从表1可以看出，本文建立的牛顿-MCG双迭代算法可以求出矩阵方程(1)的一组异类约束1-3-7解，且有很高的计算效率.当n=5时，取不同的初始矩阵，得到了不同的异类约束1-3-7解，这说明矩阵方程(1)异类约束1-3-7解不唯一，这也是牛顿-MCG算法的特点，不要求方程解唯一，只要求方程(1)有解即可.