求解广义Nash均衡问题的同伦方法

范晓娜， 陈 燕， 蒋 俐

(南京邮电大学 理学院， 江苏 南京 210023)

广义Nash均衡问题(GNEP)由经典Nash均衡问题发展而来. 不同之处在于广义Nash均衡问题中的每一位博弈者的决策都不仅依赖于自身的决策变量，还取决于其他博弈者所做的决策. 因此广义Nash均衡问题更具有现实意义，更适用于模拟竞争市场的真实状况. 随着对广义Nash均衡问题的深入研究，广义Nash均衡在金融经济、政治、军事、电子通信、生物科技、工程技术、环境和交通运输等众多社会领域都有其广泛的应用价值. 不可否认的是，当前对广义Nash均衡问题的研究还远不如对经典Nash均衡问题的研究那样丰富和完善. 2009年，Xu、Yu[1]等人在有界域内用同伦方法对GNEP进行研究和求解，该方法克服了已有方法(文献[2—5])的收敛困难、收敛条件强等缺点，得到了较好的收敛结果. 2019年，Fan[6]等在文献[1]的基础上给出一种新的同伦方法求解GNEP，该方法扩大了初始点的选取范围，为问题的解决带来了方便. 本文考虑改进文献[6]的结果，通过引入两个辅助映射，从而扩大收敛的范围并加快收敛的速度.

1 预备知识

考虑一个共有N人的非合作博弈，每个博弈者的决策集不仅依赖于自身的决策变量，还取决于其他博弈者所做的决策.给定一个集值映射Xi:

x=(x1,…,xi,…,xN)T=(xi,x-i)T,xi∈Rni.

对任意x-i∈Rn-i，gi:Rn→Rmi,hi:Rni→Rli,第i个博弈者的决策集记为Xi(x-i)≡{xi∈Rni:gi(x)≤0,hi(xi)=0}.记指标集为

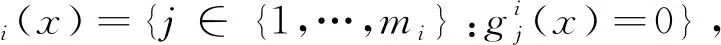
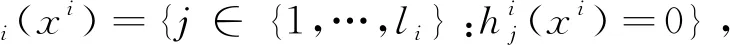
其中

Xi(x-i)的内部记为Xi(x-i)0≡{xi∈Rni:gi(x)<0,hi(xi)=0}，边界集记为∂(Xi(x-i))≡{xi∈Rni:gi(x)=0,hi(xi)=0，j∈Ii(x)}.

对于GNEP，每个博弈者做出的决策都依赖于其他玩家的决策.当其他竞争对手的决策确定以后，第i个博弈者的目标就是要选择一个决策xi解决最优化问题:

其中ui称为第i个博弈者的效用函数.

为了简化起见，本文引用以下符号

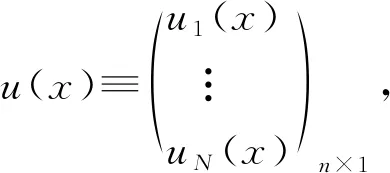
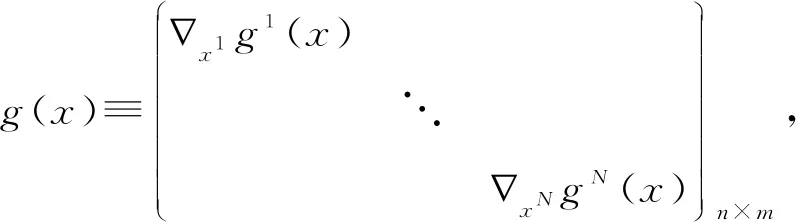
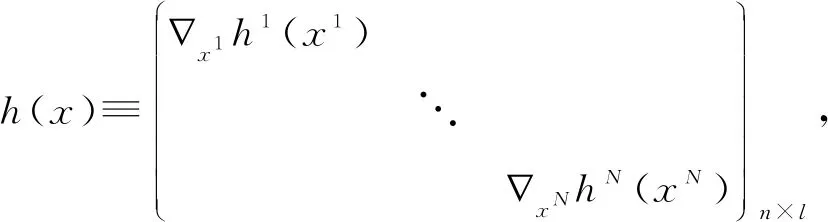
其中m=m1+…+mN,l=l1+…+lN,n=n1+…+nN.

2 同伦方程的构造

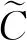
基于KKT系统:

(1)

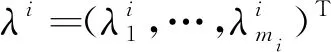
H(ω,ω(0),μ)=

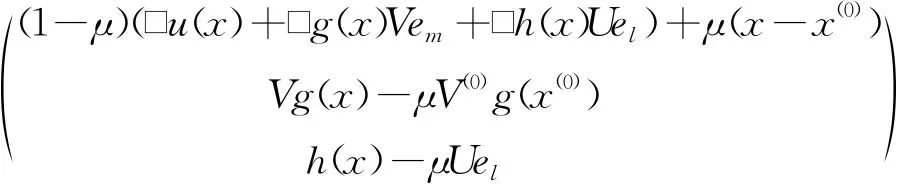
(2)

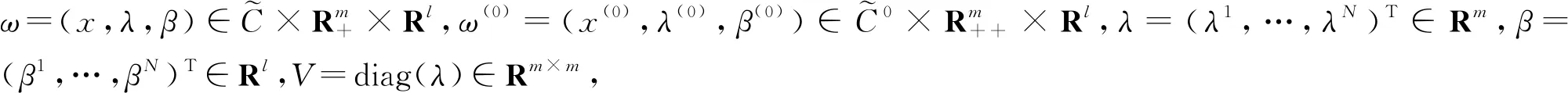
在一定的假设条件下，同伦路径的存在性和收敛性可以得到证明.

从而得到x=x(0)，β=β(0)=h(x(0))，由于g(x(0))<0，故λ=λ(0).因此,方程H(ω,ω(0),1)=0有唯一解ω=ω(0).当μ=0时，上述同伦方程即简化为GNEP中的KKT系统.

为得到本文的主要结果，先介绍以下引理.

则y∈Rp是φ的一个正则值.

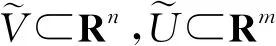
引理3(一维光滑流形分类定理)[8]一维光滑流形与单位圆或单位区间同胚.

假设1

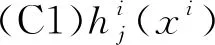
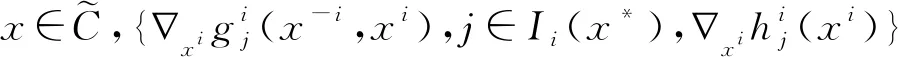
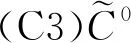
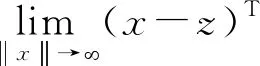
3 主要结果

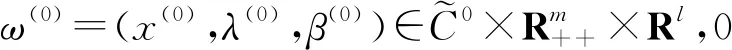
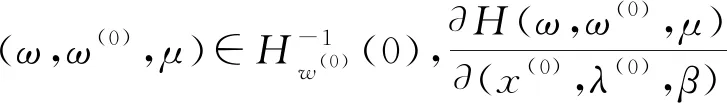
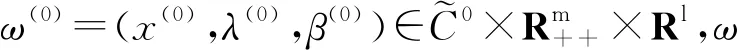
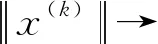
(4)

将(4)式的第1个方程变形，并在等式两边同时乘以(x(k)-z)，z∈C，则有

(x(k)-z)T(□u(x(k))+μkα(x(k))V(k)2em+

μkγ(x(k))U(k)2el)=

(x(k)-z)T□g(x(k))V(k)em-

(x(k)-z)T□h(x(k))U(k)el，

即

(z-x(k))T(□u(x(k))+

μkα(x(k))V(k)2em+μkγ(x(k))U(k)2el)=

(x(k)-z)T□g(x(k))V(k)em+

(x(k)-z)T□h(x(k))U(k)el≥

(g(x(k))-g(z))TV(k)em+

(h(x(k))-h(z))TU(k)el=

μkg(x(0))TV(0)em-g(z)TV(0)em+

μkelTU(k)TU(k)el≥

μkg(x(0))TV(0)em+μkelTU(k)TU(k)el=

(1-μk)g(x(0))TV(0)em+

(1-μk)elTU(k)TU(k)el]=

(1-μk)g(x(0))TV(0)em+

(1-μk)elTU(k)TU(k)el].

根据函数g的凸性和h的线性性质可推出第一个不等式，即

(x(k)-z)T□g(x(k))=

(x(k)-z)T□h(x(k))=

由方程(4)的第2个式子可推出第2个等式，推导如下：

(g(x(k))-g(z))TV(k)em=

(g1(x(k))-g1(z),…,gm(x(k))-gm(z))×

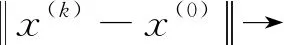
(1-μk)g(x(0))TV(0)em+

(1-μk)elTU(k)TU(k)el>M，

故(z-x(k))T(□u(x(k))+μkα(x(k))V(k)2em+

μkγ(x(k))U(k)2el)>0，即(x(k)-z)T(□u(x(k))+μkα(x(k))V(k)2em+μkγ(x(k))U(k)2el)<0，这与假设(C4)矛盾，因此ω的分量x是有界的.

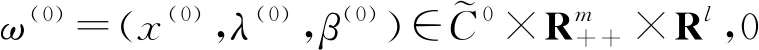
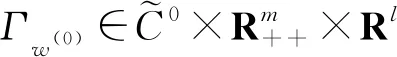
(1-μk)(∇xiui(x(k,-i),x(k,i))+∇xigi(x(k,-i),x(k,i))λ(k,i)+

μkαxi(x(k,-i),x(k,i))(λ(k,i))2+∇xihi(x(k,i))β(k,i)+

μkγxi(x(k,-i),x(k,i))(β(k,i))2)+μk(x(k)-x(0))=0.

(5)

对于μ*∈[0,1]，分以下两种情况讨论β(k)的有界性：

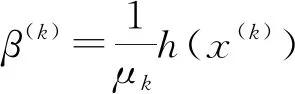
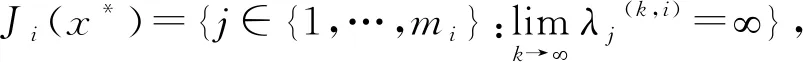
方程(5)可改写为

(1-μk)∇xiui(x(k,-i),x(k,i))+μk(x(k,i)-x(0,i))+

μkγxi(x(k,-i),x(k,i))(β(k,i))2]=0.

(6)

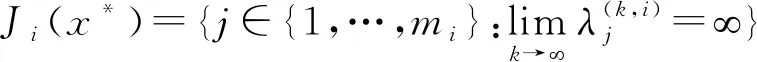
(ⅰ)当μ*=1时，将(5)式改写为

μk(x(k,i)-x(0,i))=

(7)

根据引理5以及上述分析，令k→∞，x(k)→x*，β(k)→β*，由(7)式得

(8)

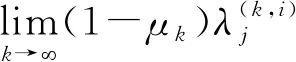
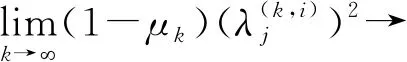
与假设(C2)矛盾.

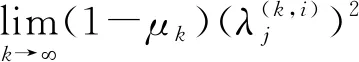
从而x(*,i)+υαxi(x(*,-i),x(*,i))=x(0,i)，与假设(C5)矛盾.

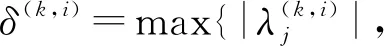
这与假设(C2)矛盾.

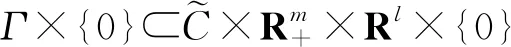
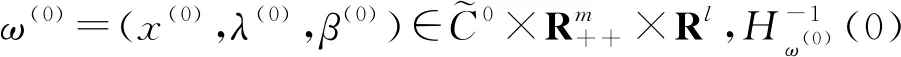
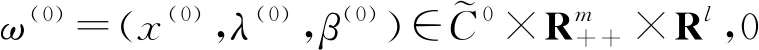
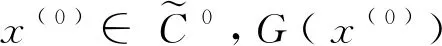
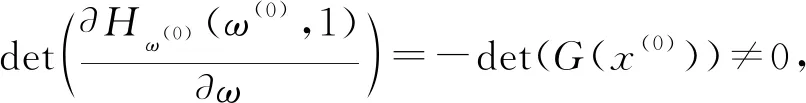
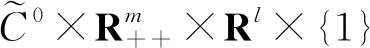
(9)

拆分(9)式的第1个等式，我们得到以下结果.

定理2同伦路径Γω(0)由以下常微分方程组的初值问题决定:

且对于μ(s*)=0，方程(9)的解(ω(s*),μ(s*))的分量x是GNEP的解.

根据定理1和定理2，可以用标准预估矫正法对同伦路径Γω(0)进行数值追踪，从而找到同伦方程(3)的解.

4 数值例子

在MATLAB中用Euler Newton算法对同伦路径进行追踪，并将产生的结果与已有的同伦方法作比较.对以下所有算例，选取相同的精确度参数：ε1=10-4,ε2=10-1,ε3=10-6,μ0=1.0.数值结果见表1和表2，其中A1表示本文构建的同伦方法，A2表示文献[6]中所用的同伦方法.IT表示迭代次数，CPU表示程序运行时间，x0表示初始点，x*表示问题的近似解. 数值结果表明本文的同伦方法对于求解GNEP是有效的.

表1 例1的数值结果

表2 例2的数值结果

例1

例2

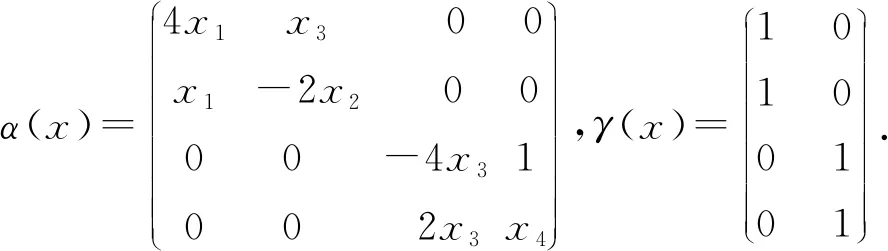
例3

x1+x2=1;

x3+x4=1.

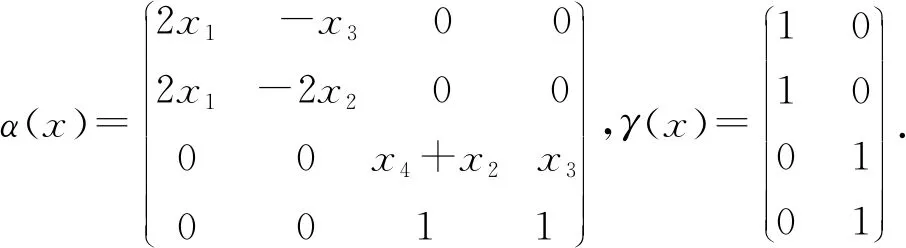
表3 例3的数值结果

5 结语

对于求解带有等式和不等式约束的GNEP，本文通过引入2个二次连续可微映射α(x)，γ(x) 构造出一个新的同伦方程，并在给出的假设条件下，证明了同伦路径的存在性和全局收敛性.相较于文献[1]中的同伦方法，本方法同样减弱了收敛的条件，扩大了初始点的选取范围，并且相较于文献[6]中的同伦方法具有更高的计算效率. 数值例子证明了新的同伦方法的有效性.