交超格上的素超理想定理

赵雪欣, 谢祥云

(1.五邑大学 数学与计算科学学院， 广东 江门 529020; 2.江门职业技术学院 教育系， 广东 江门 529030)

超结构理论最初是由F.Marty在1934年第八届数学家代表大会上提出的[1].从那以后,超代数系统理论被应用到很多方面.例如,文献[2]研究了超群,文献[3]对超环进行了研究,文献[4]提出了超BCK-代数.超结构理论在纯应用科学的许多领域都有应用,包括几何学、图论、模糊集、粗糙集、自动机和码等[5].

超格理论是由Konstantinidou和J.Mittas在1977年提出的[6].随后文献[7]研究了超格和子超格理论，文献[8—9]研究了分配超格与超格中的理想，文献[10]研究了超格的直积.此外,文献[11]讨论了分配超格上的素理想定理，文献[12]讨论了超格上的素滤子以及理想与滤子的等价刻画，文献[13]探讨了强交超格上的理想和超滤子,并研究了强交超格上的素超滤子定理.

本文介绍交超格上超理想的概念并研究超理想的相关性质,然后探讨带“*”条件的交超格并在此基础上给出素超理想定理.

1 预备知识

本节给出需要用到的交超格的一些性质.

定义 1[1]设Δ是一个非空集合,P(Δ)表示非空集合Δ的幂集,P*(Δ)=P(Δ)-∅.映射f:Δ×Δ→P*(Δ)称为Δ上的超运算.

定义 2[13]设L是一个非空集合,“∧”和“∨”分别是L上的超运算和普通二元运算.若对任意的a,b,c∈L,满足

(ⅰ)a∈a∧a,a=a∨a，

(ⅱ)a∧b=b∧a,a∨b=b∨a，

(ⅲ)(a∧b)∧c=a∧(b∧c),(a∨b)∨c=a∨(b∨c)，

(ⅳ)a∈[a∧(a∨b)]∩[a∨(a∧b)]，

则称L为交超格.进一步,若再满足

(ⅴ)a∈a∧b⟹a∨b=b，

则称交超格L为强交超格.

对任意的A,B∈P*(L),记A∧B=∪{a∧b|a∈A,b∈B},A∨B={a∨b|a∈A,b∈B},特别地,若B={b},则A∧B记为A∧b.

由定义2知,若a,b∈L且a=a∨b,则

b∈[b∧(a∨b)]∩[b∨(a∧b)]=

(a∧b)∩[b∨(a∧b)],

因此b∈a∧b.

进一步地,我们在L上定义二元关系“≤”:

(∀a,b∈L)a≤b⟺b=a∨b.

容易证明,“≤”为L上的一个偏序关系.在(L,≤)中,若存在最小元,则记为0;若存在最大元,则记为1.

若存在0,1∈L,即(∀x∈L)0≤x≤1，则称交超格L为有界的.

定义 3[13]设L为交超格,

(ⅰ)若对于任意的a,b,c∈L,

a∨(b∧c)=(a∨b)∧(a∨c),

则称交超格L为分配的.

(ⅱ)若对于任意的a,b,c∈L,

a∧(b∨c)=(a∧b)∨(a∧c),

则称交超格L为对偶分配的.

引理1设(L,∧,∨)是一个交超格,则下列命题成立:

(ⅰ)对任意的a,b∈L,存在a1,b1∈a∧b,使得a1≤a,b1≤b，

(ⅱ)若L是强交超格且a∧b=L,则a=b，

(ⅲ)若a∧b={1},则a=b=1，

进一步地,若L是分配的且有最大元1,则

(ⅳ)1∧1={1}，

(ⅴ)对任意的a∈L,a是a∧a中的极小元.

证明(ⅰ)～(ⅲ)的证明见文献[13].

(ⅳ)因为1是最大元,所以有

{1}=1∨(a∧b)=(1∨a)∧(1∨b)=1∧1.

(ⅴ)设a∈L,且x∈a∧a使得x≤a,则

x∨a=a,

(x∨a)∧(a∨a)=a∧a=(x∧a)∨a.

因此，存在y∈x∧a,使得x=y∨a≥a,故x=a.

2 主要结果

本节主要给出交超格上的素超理想定理.

定义4设I是交超格L上的一个非空子集,若

(ⅰ)(∀x,y∈I)x∨y∈I,

(ⅱ)(∀x∈I,y∈L)x∧y⊆I且(∀a∈x∧y)a≤x,

则称I为超理想.若对任意的a∈x∧y,a≤x,则记为x∧y≤x.若超理想I满足

(∀x,y∈L)x∧y⊆I⟹x∈I或y∈I,

则称超理想I为素的.

性质1设I是交超格L上的一个超理想,若x∈I,y∈L且y≤x,则y∈I.

证明由定义2知

y∈[y∧(x∨y)]∩[y∨(x∧y)]=

(x∧y)∩[y∨(x∧y)],

因此y∈x∧y⊆I.

定义5[13]设F是交超格L上的一个非空子集,若

(ⅰ)∀x,y∈F⟹x∧y⊆F,

(ⅱ)∀x∈F,y∈L,x≤y⟹y∈F,

则称F为超滤子.对于超滤子F,若(∀x,y∈L)x∨y∈F⟹x∈F或y∈F,则称超滤子F为素的.

例1设L={0,a,1},定义L上的∧-超运算和∨-运算(表1～表2),则(L,∧,∨)是一个有界的交超格,{0,a}是L上的超理想.

表1 L上的∧-超运算(例1)

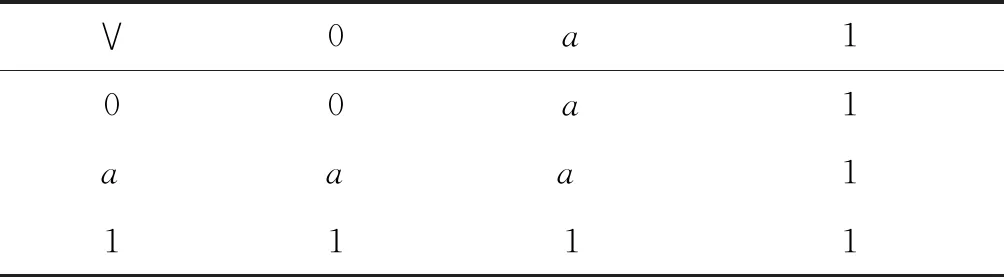
表2 L上的∨-运算(例1)

例2设L={0,a,b,1},定义L上的∧-超运算和∨-运算(表3～表4),则(L,∧,∨)是一个交超格.{0,a}是L上的素超理想,由a∧b={0}和a,b∉{0}知{0}是超理想但不是素的;{b,1}既不是超理想也不是超滤子;{1}是L上的超滤子但不是素的.

表3 L上的∧-超运算(例2)

表4 L上的∨-运算(例2)

例3设L={0,a,b,c,1},定义L上的∧-超运算和∨-运算(表5～表6),则(L,∧,∨)是一个交超格.{0,b,c}是L上的素超理想,{0,c}是超理想但不是素的;{a,1}是L上的素超滤子,{1}是超滤子但不是素的.

表5 L上的∧-超运算(例3)

表6 L上的∨-运算(例3)

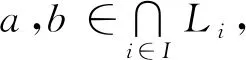
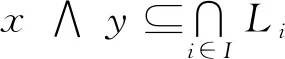
定理2设I和J是L的超理想,则I∪J是L的超理想当且仅当I⊆J或者J⊆I.

证明″⟸″.若I⊆J或J⊆I,则有I∪J=J或I.因此I∪J是L的一个超理想.

″⟹″.若I∪J是L的一个超理想,则有I⊆J或J⊆I.事实上,若I⊄J且J⊄I,则存在a∈IJ,b∈JI.由假设知a,b∈I∪J且a∨b∈I∪J,若a∨b∈I,则b≤a∨b∈I,从而b∈b∧(a∨b)⊆I,矛盾;若a∨b∈J,则a≤a∨b∈J,因此a∈a∧(a∨b)⊆J,矛盾.

定理3设L是一个对偶分配交超格,I和J是L的超理想,定义

I∨J={x∈L|(∃a∈I)(∃b∈J)x=

a∨b},

则I∨J是L的超理想.

证明若x,y∈I∨J,则存在a1,a2∈I,b1,b2∈J使得x=a1∨b1,y=a2∨b2.因此

x∨y=(a1∨b1)∨(a2∨b2)=

(a1∨a2)∨(b1∨b2).

因为I和J是L的超理想,从而a1∨a2∈I和b1∨b2∈J,所以x∨y∈I∨J.

若x∈I∨J,y∈L,则存在a1∈I,b1∈J使得x=a1∨b1.因此

x∧y=(a1∨b1)∧y=(a1∧y)∨(b1∧y),

从而对任意t∈x∧y,存在t1∈a1∧y,t2∈b1∧y使得t=t1∨t2.因为a1∈I,b1∈J,从而a1∧y⊆I,b1∧y⊆J,所以t1∈I,t2∈J,因此t∈I∨J,x∧y⊆I∨J.

另一方面,因为t=t1∨t2,t1∈a1∧y,a1∈I,所以t1≤a1.类似地,由t2∈b1∧y可得t2≤b1,因此t=t1∨t2≤a1∨b1=x,即x∧y≤x.

定义6设L是一个交超格,若

(∀x,y∈L)∀t∈x∧y⟹t≤x,t≤y,

(*)

则称L为一个满足条件“*”的交超格.

特别地,若L是一个格,则L是一个带“*”条件的交超格.进一步地,若(L,∨,∧)是一个∧-超格,其中L上的∧-超运算定义为a∧b={x∈L|x≤a,x≤b},则(L,∨,∧)是一个带“*”条件的交超格,inf{a,b}是a∧b的最大元.显然例1～例3都是一个带“*”条件的交超格.

定理4设L是一个带“*”条件的交超格,则I={x∈L|x≤a}是L上的一个超理想,记为I(a).

证明对任意x,y∈I,x≤a,y≤a,有x∨a=a,y∨a=a.于是

x∨a∨y∨a=x∨y∨a=a∨a=a.

因此x∨y≤a,x∨y∈I.

另一方面,对任意的x∈I,y∈L,有x≤a.由定义6知,对任意的t∈x∧y,t≤x≤a,因此t∈I,x∧y⊆I且x∧y≤x.

定理5设L是一个带有最小元0的交超格,I是L的一个超理想,则0∈I.

证明因为I是L的一个超理想,所以对任意的a∈I,由性质1知0≤a,从而0∈I.

引理2设L是一个满足条件“*”且带有最小元0的对偶分配交超格,若I是L的超理想,且a∈L但a∉I,则I∨I(a)是一个超理想且I⊂(I∨I(a)).

证明根据定理4可知I(a)是L的一个超理想,再由定理3知我们只需证明I⊂(I∨I(a)).

事实上,∀x∈I,x=x∨0∈(I∨I(a)),所以I⊆(I∨I(a)).但a∉I且a=0∨a,由定理5知0∈I且a∈I(a),所以a∈(I∨I(a)).

最后给出下列素超理想定理.

定理6设(L,∧,∨)是一个带有最小元0的对偶分配交超格,且满足条件“*”.若I和F分别是L的超理想和超滤子使得I∩F=∅,则存在L的一个素超理想D使得I⊆D且D∩F=∅.

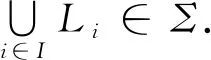
下面证明D是L的一个素超理想.事实上,假设a,b∈L,a∧b⊆D且a,b∉D.因为D是极大理想,由引理2知[D∨I(a)]和[D∨I(b)]是L的超理想,且有

[D∨I(a)]∩F≠∅, [D∨I(b)]∩F≠∅.

从而存在d1,d2∈D,a1∈I(a),b1∈I(b)使得d1∨a1∈F,d2∨b1∈F.因为a1≤a,b1≤b,所以

d1∨a1≤d1∨a,d2∨b1≤d2∨b,

从而d1∨a,d2∨b∈F,因为F是一个超滤子,所以(d1∨a)∧(d2∨b)⊆F,由L的对偶分配性知

(d1∨a)∧(d2∨b)=

[(d1∨a)∧d2]∨[(d1∨a)∧b]=

(d1∧d2)∨(a∧d2)∨(d1∧b)∨

(a∧b)⊆D,

从而D∩F≠∅,矛盾.