次分数跳扩散过程下亚式期权的保险精算定价

胡 攀

(四川文理学院 数学学院,四川 达州 635000)

亚式期权作为一种强路径依赖性新型期权,其价格取决于期权到期前一段时间内或整个有效期内的平均值[1]. 相比于普通期权,亚式期权的波动较小, 能较好地规避投资风险,深受投资者喜爱.亚式期权,按照合同中买卖标的资产来划分可分为看涨和看跌两种; 按照其平均值的不同计算方式可分为算术平均和几何平均两种; 按照其执行价格又可分为固定执行价格和浮动执行价格两类.

基于经典BS模型的亚式期权定价[2—3], 假设标的资产价格是一个连续扩散过程,且利率和波动率均为常数, 由此得到的定价结果与真实值之间存在较大偏差.对此许多学者做了大量的改进研究, 主要体现在以下3个方面：①对利率和波动率的改进模型[4—5];②在连续扩散模型基础上考虑存在 “跳跃”的情况[6]; ③对连续扩散项的改进, 主要考虑股票价格遵循分数布朗运动、双分数布朗运动以及混合分数布朗运动的亚式期权定价问题[7—8]. 2004年Bojdecki[9]等建立了比分数布朗运动更一般的中心高斯过程——次分数布朗运动. 2007年Tudor[10]研究发现次分数布朗运动的退化速度优于分数布朗运动, 能更好地刻画标的资产的长记忆性. 基于次分数布朗运动模型下的期权定价问题参见文献[11—12]. 2019年胡攀[13]在次分数Ho-Lee随机利率模型假设下,利用△对冲原理，建立了次分数跳-扩散过程下带有红利支付和交易成本的几何平均亚式期权的偏微分方程模型，并利用有限差分法和复合梯形法给出了定价模型的数值解.最后,通过数值模拟验证了解法的有效性.

1998年, Bladt和Rydberg[14]提出了将期权定价转化为公平保费确定问题的保险精算法. 由于该方法不仅对完备、均衡和无套利的市场有效, 而且对不完备、非均衡和有套利的市场也有效. 因此, 自从该方法被提出以后, 已然成为一种高效的期权定价方法. 基于保险精算法的期权定价问题参见文献[15—16].

本文考虑具有浮动执行价格和固定执行价格的几何平均亚式期权的定价问题, 在次分数跳扩散机制下, 利用保险精算法给出看涨、看跌期权的定价公式及二者之间的平价关系.最后，以次分数跳扩散过程下具有固定执行价格的几何平均亚式期权为例,通过数值模拟讨论模型参数对期权价值的影响.

1 预备知识

cov[WH(t),WH(s)]=

(1)

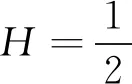
假设金融市场无摩擦, 其中有两种资产: 一种是无风险债券, 其价格过程Pt满足

dPt=rPtdt；

(2)

另一种是风险资产(如股票), 其价格过程{St，t≥0}遵循如下次分数跳-扩散过程：

dSt=

St[(μ-q-λθ)dt+σ0dWH(t)+JtdNt],

(3)

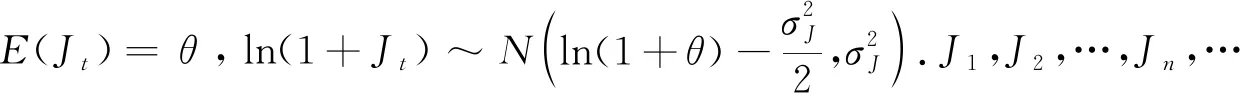
定义1[13]标的资产价格{Su，u≥0}在[0,t]时间段内的期望收益率βu定义为

即风险资产在[0,t]的期望收益率定义为风险资产期末价格的期望与初始价格之比.

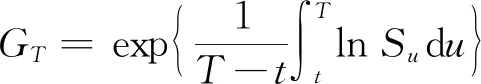
C(Gt,St,t)=

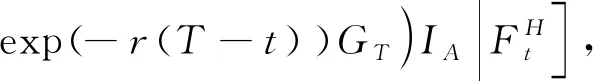
(4)

P(Gt,St,t)=

(5)

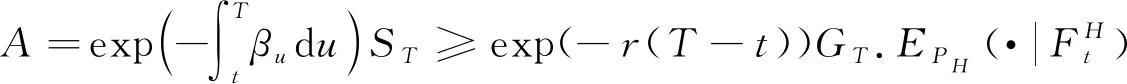
定义3固定执行价格为K的几何平均亚式看涨、看跌期权在任意时刻t∈[0,T]的保险精算价格定义为

C(Gt,St,t)=

(6)

P(Gt,St,t)=

(7)

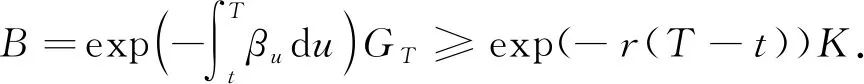
定义2与定义3中期权的保险精算价格定义为风险资产价格按期望收益率折现，无风险资产价格按无风险利率折现的期望收益.

引理1标的资产价格{St，t≥0}满足(3)式, 其解为

(8)

证明假设标的资产价格{St，t≥0}在随机时间t1,t2,…,tn,…处发生跳跃,对应的跳跃高度分别为J1,J2,…,Jn,…, 在相邻的两次跳ti，ti+1之间,St遵循次分数BS模型.跳跃时间tn服从参数为λ的Poisson过程. 在[ti,ti+1)上有

dSt=St[(μ-q-λθ)dt+σ0dWH(t)].

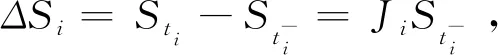
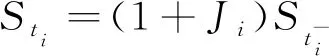
对∀t∈[t1,t2)有

从而

重复上述迭代过程, 并考虑在[0,t]内股票价格没有发生跳跃的情况即可得引理结论.

证明由于Jt与WH(t)相互独立, 根据(8)式可得

又

(9)

(10)

从而

由定义1即得结论.

引理3[17]设随机变量Y1,Y2∈N(0,1) , 且cov(Y1,Y2)=ρ，则

(11)

其中N(·)为标准正态分布函数.

2 几何平均亚式期权的保险精算定价

定理1次分数跳扩散过程下, 到期时间为T,具有浮动执行价格的几何平均亚式看涨、看跌期权在时刻t∈[0,T]的价格为

C(Gt,St,t)=

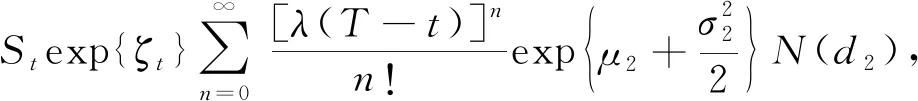
(12)

P(Gt,St,t)=

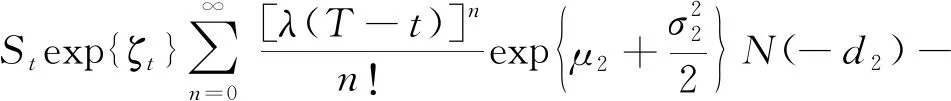
(13)

其中

(14)

(15)

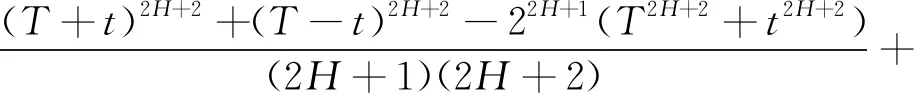
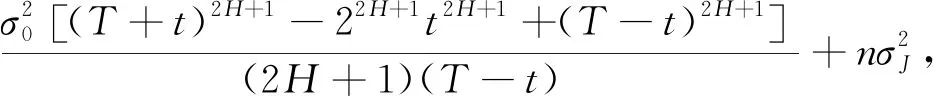
(16)

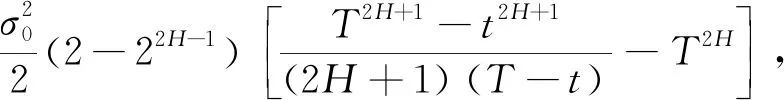
(17)

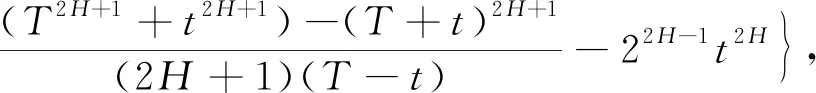
(18)

(19)

ξt=-λ(θ+1)(T-t)-

(20)

(21)

证明记Nt,T=NT-Nt，根据(8)式可得

由定义2得

C(Gt,St,t)=

(22)

记

显然,在给定Nt,T=Nt,u=n的条件下，

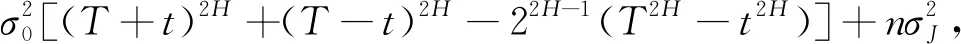
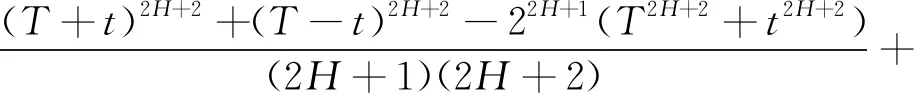
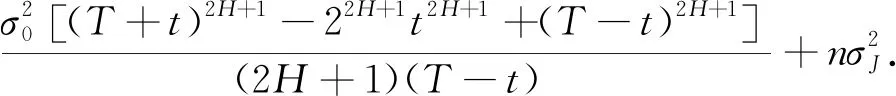
由A=exp{-β(T-t)}ST≥exp{-r(T-t)}GT,两边取对数得X1-X2≥k，其中

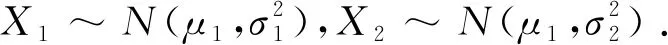
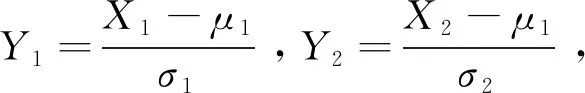
ρ=

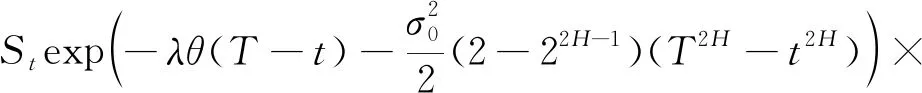
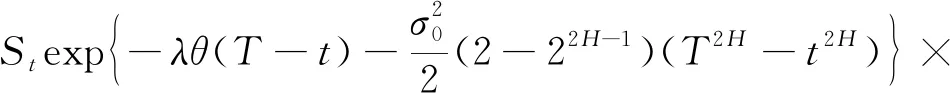
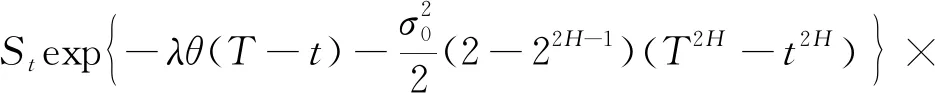
利用引理3的结果可得

记

ξt=-λ(θ+1)(T-t)-

即得(12)式的第一部分.同理可得

I2=

其中d2，ζt见(19)、(21)两式.将I1,I2的结果代入(22)式可得看涨期权的定价公式.

看跌期权的定价公式可类似证明.

定理2次分数跳扩散过程下, 到期时间为T,具有浮动执行价格的几何平均亚式看涨、看跌期权在时刻t∈[0,T]的平价关系为

C(Gt,St,t)-P(Gt,St,t)=

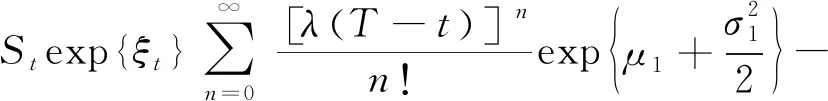
(23)

证明利用累积标准正态分布的对称性N(-x)=1-N(x), 对公式(13)进行化简即得定理结论.

类似定理1和定理2的证明,可证固定执行价格几何平均亚式看涨、看跌期权的定价公式和平价关系.

定理3次分数跳扩散过程下, 到期时间为T,执行价格为K的几何平均亚式看涨、看跌期权在时刻t∈[0,T]的价格为

C(t,Gt,K)=

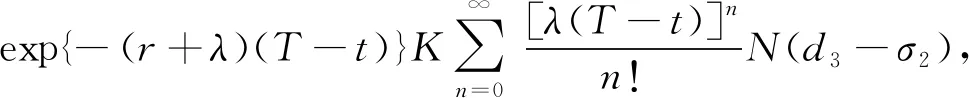
(24)

P(t,Gt,K)=exp{-(r+λ)(T-t)}×

N(-d3)，

(25)

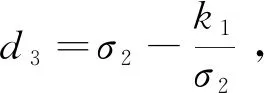
定理4次分数跳扩散过程下, 到期时间为T,执行价格为K的几何平均亚式看涨、看跌期权在时刻t∈[0,T]的平价关系为

C(t,Gt,K)-P(t,Gt,K)=

exp{-(r+λ)(T-t)}K.

(26)

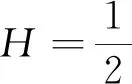
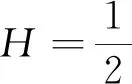
3 数值模拟

本节以次分数跳扩散模型下具有固定执行价格的几何平均亚式期权为例，通过数值模拟讨论Hurst指数H,跳跃强度λ和到期时间T对期权价格的影响.

3.1 数值模拟的基本步骤

第一步：由(24)～(25)式可知，固定执行价格几何平均亚式期权的定价模型均为数项级数的代数和，利用优级数判别法和比值判别法，容易验证两个模型均收敛；

第二步：置n=0，并设定模型中除Hurst指数H,跳跃强度λ和到期时间T外的其他参数；

第三步：对Hurst指数H,跳跃强度λ和到期时间T分别取不同值，代入(24)～(25)式，计算与级数前n项和前n+1项对应的期权价格；

第四步：以10-5为绝对误差限，若第三步中计算出的期权价格的绝对误差小于10-5，则停止迭代，输出期权价格、收敛项数和绝对收敛误差，否则，令n=n+1，返回第三步.

3.2 数值模拟结果

设置模型中的相应参数如下：t=0,S0=10,σ0=0.4,r=0.05,q=0.01,μ=0.06,θ=0.3,σJ=0.2,K=10.Hurst指数H，跳跃强度λ和到期时间T的取值及期权价格的计算结果见表1.

表1给出了次分数条件下，具有固定执行价格的几何平均亚式看涨、看跌期权的价格计算结果，及绝对误差限为10-5时，期权价格收敛的项数和收敛误差.计算结果表明：

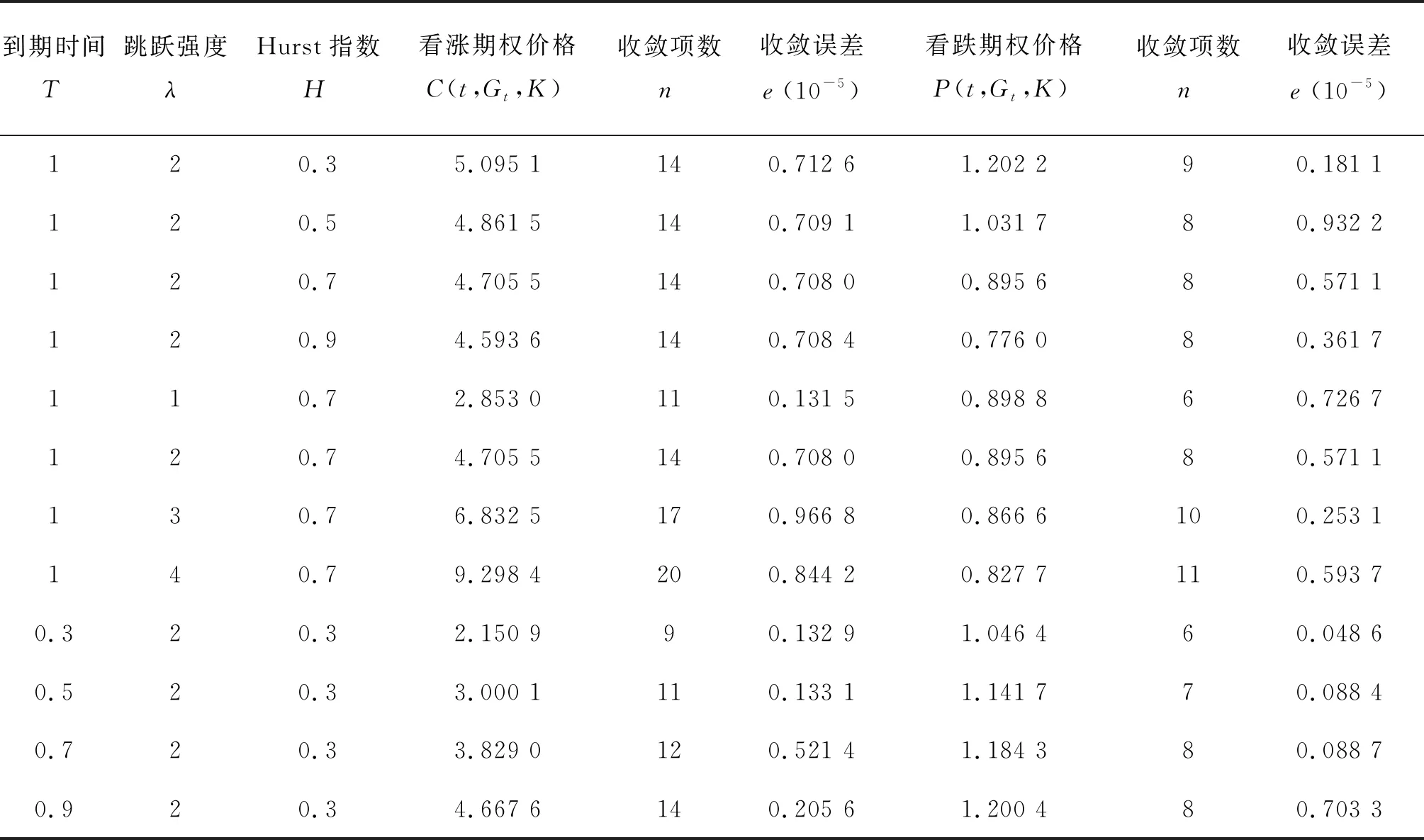
表1 次分数跳扩散过程下亚式看涨、看跌期权的数值模拟结果

(ⅰ)在参数给定的条件下，次分数跳扩散过程下具有固定执行价格的几何平均亚式看涨期权的价格要高于看跌期权的价格，价格高出的部分可由期权的平价关系式(26)给出合理解释，即看涨期权价格高出看跌期权价格的部分为

Kexp{-(r+λ)(T-t)}.

(ⅱ)在其他参数固定的情况下,亚式看涨、看跌期权的价格随着Hurst指数H的增加而减小,这表明几何平均亚式看涨、看跌期权价格是Hurst指数H的减函数.

(ⅲ)给定其余参数的条件下，标的资产价格的跳跃强度λ增加，看涨期权的价格增加，看跌期权的价格降低. 这是因为：一方面，当Hurst指数H=0.7∈(0.5,1)时，标的资产价格具有持久性和自相似性.持久性表现为:若前一阶段股价走高，则下一阶段也走高，反之亦然.当标的资产价格由于持久性持续升高时，看涨期权的价格升高，看跌期权的价格反而降低;另一方面，标的资产的跳跃强度λ增大，标的资产的波动就增加，由于标的资产的收益率μ=0.06>0，所以标的资产的这种波动不会影响其价格的大致走势，尽管投资者面临的风险在变大，但是亚式期权的价格变化主要依赖于标的资产价格的走势.因此，几何平均看涨期权的价格升高，看跌期权的价格反而降低.

(ⅳ)在其余参数固定的条件下，几何平均亚式看涨、看跌期权的价格随着到期时间T的增加而增加.这是因为期权作为一种合约，是有时间价格的，随着期权剩余时间的增加，期权价格也增加.

(ⅴ)几何平均亚式看涨看跌期权的收敛性和收敛误差与模型中的参数密切相关.

4 小结

在市场无摩擦且Hurst指数H∈(0,1)的假设下, 在标的资产价格服从次分数跳扩散过程时, 利用保险精算法建立了带有红利支付的浮动执行价格和固定执行价格几何平均亚式看涨、看跌期权的定价公式, 并给出了看涨、看跌期权的平价关系.数值模拟的结果显示, 在其他参数固定的情况下,几何平均亚式看涨、看跌期权的价值与Hurst指数H呈反变关系,与到期时间T均成正变关系，看涨期权价格与跳跃强度λ成正比，看跌期权价格与跳跃强度λ成反比,期权价格的收敛项数与绝对收敛误差和模型参数有关.次分数跳扩散过程下几何平均亚式期权的定价模型是跳扩散过程下定价模型的推广. 定价模型中将无风险利率和标的资产的波动率视为常数并不符合实际金融市场的特点, 建立利率和波动率的改进模型是后续研究的主要内容.