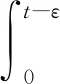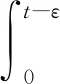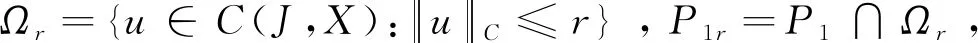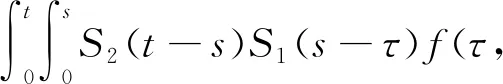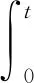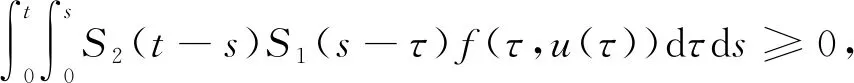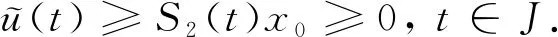Banach空间中阻尼弹性系统正mild解的存在性

王倩倩

(兰州交通大学 数理学院， 甘肃 兰州 730070)

对阻尼弹性系统结构的研究, 是结构力学和数学领域的热点之一, 这不仅是因为它具有较高的理论价值, 而且还有着广阔的应用背景. 例如, 振动改进和控制在维持高性能与生产效率, 延长工业机械有效寿命方面起着关键性的作用. 自1982年以来, 国内外许多学者对具有阻尼的弹性系统

u″(t)+Bu′(t)+Au(t)=0，

(1)

在Hilbert空间H中进行了卓有成效的研究, 就该系统相应解半群的可微性、解析性及该系统的谱性质获得了一系列重要结果(见文献[1-5]).

近年来, 文献[6—9]在Banach空间框架下利用算子半群理论和不动点理论等工具, 研究了初值问题(1)相应解半群的解析性与指数稳定性、mild解的存在唯一性及全局mild解的渐近行为. 据我们所知, 鲜有文献利用锥上的不动点定理研究初值问题(1)正mild解的存在性. 因此, 本文的结论在一定意义上丰富了阻尼弹性系统已有的工作.

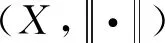
(2)

正mild解的存在性, 其中ρ≥2是阻尼系数,A:D(A)⊂X→X是闭线性算子, -A生成X上的C0-半群T(t) (t≥0),f:[0,a]×X→X为非线性映射,x0∈D(A),y0∈X.

1 预备知识

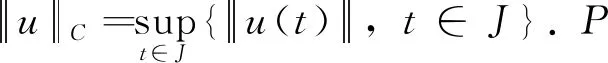
P1={u∈C(J,X)|u(t)≥0, ∀t∈J},

则P1为C(J,X)中的一个锥, 其中0为X中的零元.

以下列出本文用到的主要定义和引理.

定义1[8]设X是实Banach空间, 若P是X中某非空凸闭集, 并且满足下面2个条件:

(ⅰ)x∈P,λ≥0⟹λx∈P，

(ⅱ)x∈P, -x∈P⟹x=0,

则称P是X中的一个锥.

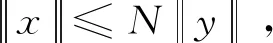
由正规锥的定义可知, 若P是X中的正规锥,N为正规常数, 则P1为C(J,X)中的正规锥, 且其正规常数为N.

定义3[9]设T(t) (t≥0)是X上的一个C0-半群, 若对于任意x>0 ,t>0均有T(t)x≥0成立, 则称C0-半群T(t) (t≥0)是正的.

定义4[9]设T(t) (t≥0)是X上的一个C0-半群, 若对于任意t>0, 算子T(t):X→X是紧的, 则称C0-半群T(t) (t≥0)是紧的.

引理1[6]设A:D(A)⊂X→X是闭线性算子, -A生成X上的C0-半群T(t) (t≥0),f:[0,a]×X→X为非线性映射, 则积分方程

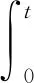
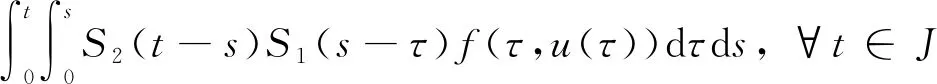
(3)

的一个连续解称为初值问题(2)的mild解, 其中S1(t) (t≥0)和S2(t) (t≥0)是由-σ1A和-σ2A分别生成的C0-半群，且满足S1(t)=T(σ1t),S2(t)=T(σ2t),t≥0.这里σ1+σ2=ρ,σ1σ2=1,v0∶=y0+σ2Ax0.

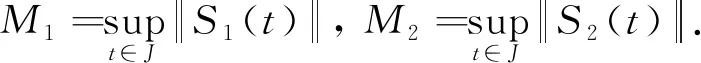
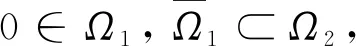
Axx, ∀x∈P∩∂Ω2,
Axx, ∀x∈P∩∂Ω1，

(4)

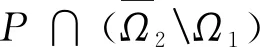
2 主要结果

根据方程(3)定义算子Q:C(J,X)→C(J,X)，满足

(Qu)(t)=

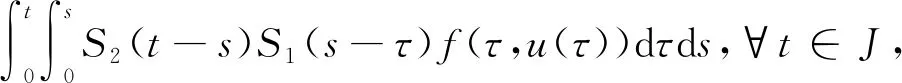
(5)

则初值问题(2)解的存在性转化为算子Q在C(J,X)上不动点的存在性.

下面给出本文所需的假设：

(H1)-A生成的C0-半群T(t) (t≥0)是紧的且是正的；

(H2)f:J×P1→P1连续, 且存在一个正的函数φ∈L∞(J,[0,+∞)), 使得

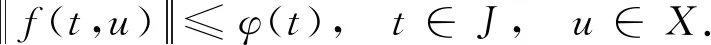
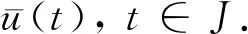
证明第一步,证明算子Q:P1→P1是连续的.

由C0-半群T(t) (t≥0)的强连续性和f的连续性可知(Qu)(t)关于t连续. 由x0>0,v0>0及条件(H1)和(H2)可知

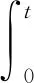
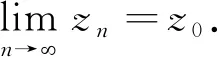
对于任意t∈J, 由f的连续性可知, 当n→∞时

所以,

第二步,证明算子Q:P1→P1是紧算子.

设有界集B⊂P1, 下证Q(B)是相对紧集. 对于任意u∈B,t∈J, 由(H2)可得

则Q(B)在J上一致有界.

对任意t1,t2∈J, 设t1

当t2→t1时, 由C0-半群按一致算子拓扑连续可知

所以,Q(B)在J上等度连续.

当t=0时,Q(B)(0)=x0为单点集; 当0

(Qεu)(t)=

因为

由S2(ε)的紧性可知, 对于任意t∈J,X中的相对紧集{(Qεu)(t):u∈B}无限逼近于集{(Qu)(t):u∈B}, 所以Q(B)(t)是相对紧的.

第三步,验证算子Q满足引理2中(4)式.

由定义3、(H1)和(H2)知

∀t∈J.

(ⅱ)取实数

由锥P的正规性知

即

这与β2的取法矛盾, 从而对于任意u∈∂P1β2,Qu