船舶舷侧与小型冰山碰撞数值模拟分析

杨碧野，黄志刚，刘宁，孙哲，张桂勇*,3,4

1 大连理工大学 船舶工程学院，辽宁省深海浮动结构工程实验室，辽宁 大连，116024 2 中汽研汽车检验中心（天津）有限公司，天津 300399 3 大连理工大学 工业装备与结构分析国家重点实验室，辽宁 大连，116024 4 高新船舶与深海开发装备协同创新中心，上海 200240

0 引 言

北极有着丰富的自然资源以及独特的战略位置，近年来，北极的开发逐渐成为国际热点[1]。在北极，冰区航路环境十分复杂，海面上存在很多尺度不一的浮冰，甚至是体积巨大的冰山和冰脊。得益于现代造船技术的发展，目前冰区航行船舶的性能及结构强度一般能够满足其在一定厚度的层冰和浮冰区内自由航行，但冰山对于极区船舶来说仍然是一种威胁。虽然船舶与冰山碰撞的概率并不大，但是一旦发生，就会给船舶结构以及船上人员安全带来危险。据Hill[2]的统计，在1619～2004 年间，共发生了约670 起船舶与冰山的碰撞事故，这些事故不但造成了人员伤亡和经济损失，还给周围环境带来了严重破坏。海冰的密度与海水非常接近，规模庞大的冰山位于海面以上部分的体积很小，隐蔽性很高，即便是借助船用雷达，也很难及时观测到这些海面上尺度较小的冰山[3]。特别是近年来随着全球气候变暖，小规模的冰山从融化的大型冰山中分离，导致航道内小型冰山出现的概率增加，因此，船舶与小型冰山的碰撞问题以及考虑碰撞载荷下船舶结构的设计问题亟待研究。

在船舶与冰山的碰撞问题中，涉及接触、大变形、流固耦合等多种复杂的非线性问题，给理论计算和数值模拟带来了挑战。为方便预测碰撞力，有学者提出了相应的理论和经验公式。Cammaert等[4]在考虑海冰挤压破坏时的能量损失的基础上，提出了浮冰或者冰山与海洋结构物碰撞的简化公式；Liu 等[5]基于Stronge 的碰撞力学模型，从外部动力学的角度提出了用于分析船−船或者船−冰碰撞的三维数学模型；Timco[6]通过分析大量的全尺度实测数据以及模型试验数据，认为海冰与海洋结构物之间碰撞力的大小与海冰的动能直接相关。这些理论或经验公式在一定程度上可以快速预测冰山与船舶的碰撞力，方便研究碰撞过程中的机理，但假设众多，过于简化，无法捕捉到碰撞中一些细节现象，并且不能满足现代船舶的需要。为了能够较为精细地模拟船舶与冰山的碰撞过程，以非线性有限元法为主的数值模拟方法在近些年逐渐得到应用。Gagnon[7]采用泡沫材料模型模拟了冰山与船舶或者海洋结构物的碰撞过程，重点模拟了冰山的压碎行为。Liu 等[8]按照Tsai-Wu屈服面准则，提出了一种适用于冰山的材料模型，并将此模型运用到了球鼻艏与冰山相撞的模拟中。Gao 等[9]分别采用弹塑性材料模型和泡沫模型对不同局部形状冰山与船体的碰撞过程进行了研究。在数值模拟中，大部分学者主要关注冰山的材料模型以及船体的结构变形，而对于碰撞过程中水的影响则考虑得并不全面，采用常数形式的附加质量系数并不能完全反映水动力的影响，而且冰山与结构物之间会出现例如波浪缓冲效应等自由液面变化。为了得到精确的结果，需要同时进行流体的计算。

本文将主要基于商业软件LS-DYNA 对小型冰山与船舶舷侧结构的碰撞进行数值模拟。首先，采用多物质任意拉格朗日−欧拉（ALE）算法进行流固耦合计算；然后，在不同碰撞角度下对船舶舷侧与冰山的碰撞过程进行仿真，同时对碰撞过程中的现象和不同工况下的碰撞力、碰撞速度以及能量吸收情况进行分析，用以指导极地船舶的建造和航行操作。

1 流固耦合算法

本文采用ALE 算法模拟冰山与舷侧结构在水中的碰撞问题。在ALE 算法中，采用欧拉方法对流体的运动和变形进行描述，而对于船体结构和冰山，则采用拉格朗日描述，并在每个时间步内进行载荷和边界的信息交换。

ALE 算法控制方程包括以下基本方程。

质量守恒方程：

式中：ρ 为材料密度；v为物质质点的速度；w为网格的速度；σ 为应力张量；g为重力加速度；e为能量；t为时间。

在流固耦合交界面处，流体与固体之间的信息传递采用罚函数法，即在每个时间步内，一旦流体节点穿过结构表面，就会产生一个耦合力Fc将贯穿的流体节点推回至耦合交界面。该耦合力的大小正比于贯穿深度d，图1 所示为该耦合算法示意图（图中，tn为第n个时间步），其中数值刚度k为：

图1 耦合算法示意图Fig. 1 Schematic diagram of coupling algorithm

式中：K为流体单元的体积模量；Vc为流体单元的体积；A为位于耦合区域结构单元的平均面积，为了避免数值不稳定，引入了罚函数系数pf（0≤pf≤ 1）。

2 海冰的材料模型

冰的本构关系十分复杂，其力学性质与应变率、温度等外在和内在物理因素有关[10-12]。在船舶与冰山的碰撞研究方面，国内外学者在冰山材料的选择上主要有3 种：双线性弹塑性模型(MAT_PLASTIC_KINEMATIC)[13]、根 据Tsai-Wu 屈 服 准则定义的弹塑性模型[8,14]，以及由Gagnon[7]提出的可压碎泡沫材料(MAT_CRUSHABLE_FOAM)。由于海冰复杂的力学性质，目前还没有一种材料模型能够完全描述海冰的力学行为，即便是上述3 种比较常见的冰山材料模型，也存在一些缺点，例如可压碎泡沫材料虽然可以模拟船舶与冰山碰撞过程中的压碎行为，但在理论上缺乏对海冰材料性质的系统描述，无法模拟海冰裂纹等问题。本文研究关注的重点是碰撞力和船体舷侧的应力变化情况。因冰山的体积较小，破坏并不是十分明显，因此将采用双线性弹塑性材料模型来模拟冰山。其中，冰山的材料参数参考文献[15]的北极冰山实验数据，如表1 所示。

表1 冰山的主要材料参数Table 1 Main material parameters of iceberg

本文将以一个球形冰与刚性板的碰撞试验为例来验证所用材料模型的可行性，图2 所示为计算工况示意图（图中虚线表示对这条线以下进行约束）。球形冰半径为2 m，球形冰远离碰撞位置的一侧刚性约束，刚性板以1 m/s 的速度与球形冰发生碰撞。海冰的压力−面积曲线常被用来记录海冰的力学性质。Kim 等[17]基于大量的试验室内海冰以及自然海冰的相关力学试验，总结得到压力−面积公式P=0.35A−0.5，如图3 中红线所示。同时，为检验网格大小对计算结果的影响，分别采 用0.1 m×0.1 m×0.1 m，0.15 m×0.15 m×0.15 m和0.2 m×0.2 m×0.2 m 这3 种不同的网格尺寸进行了数值模拟，并将记录得到的压力−面积曲线与Kim 等[17]试验所得的曲线进行了对比，如图3 所示。由图可见，3 种网格尺寸下的压力−面积关系与Kim 等[17]试验所得曲线的规律相似，并且数值模拟得到的关系曲线也基本上在经验曲线周围波动，说明了所采用材料模型的可行性。

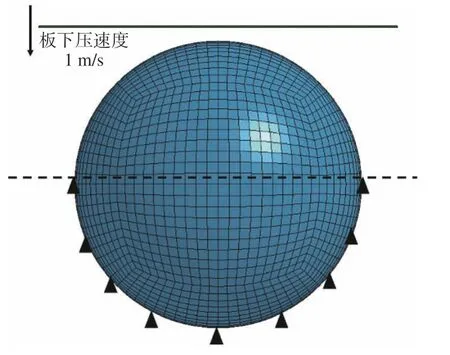
图2 球形冰与刚性板的碰撞示意图Fig. 2 Schematic diagram of the collision between spherical ice and rigid plate

图3 压力−面积曲线Fig. 3 Curves of pressure with nominal contact area

3 舷侧−冰山碰撞仿真模型

3.1 计算模型

在上述流固耦合模型以及冰材料模型的基础上，本文对船舶舷侧与小型冰山的碰撞过程进行了数值模拟。研究对象为一艘抗撞击能力较强的油船，选择船舶平行中体的部分双层舷侧结构作为计算模型。图4 所示为数值模拟中的舷侧模型，其结构包含了双层舷侧板及其之间的肋板、纵桁等构件，双层舷侧板之间的距离为1 m。整个舷侧构件使用LS-DYNA 软件中的Shell 单元进行建模，板厚按照表2 中参数。船体板的材料选择Q235 钢，材料模型同样选择MAT_PLASTIC_KINEMATIC 模型，主要材料参数如表3 所示。

图4 舷侧模型Fig. 4 Model of the side structure

表2 舷侧板的厚度Table 2 Thickness of the side shell

表3 舷侧板的主要材料参数Table 3 Main material parameters of the side shell

基于Gao 等[9]的研究成果，发现船舶与冰山碰撞时，尖锐形状的冰山在碰撞过程中容易发生破碎现象，同等条件下钝形冰的接触面将有更大的碰撞力，会对船舶造成更大的伤害，因此数值模拟中选择的是具有代表性的球形冰山。模型中，球形冰山的直径为4 m，材料模型参数如表1 所示，冰山的密度为900 kg/m3，水的密度为1 025 kg/m3，对应的冰山露出高度约为0.81 m。在建立水域和空气域时，保证两者的交界面与船舶吃水线位置相同。船舶吃水为9 m，流体计算域尺度大于双侧舷侧和球形冰山的尺度，且流体域要在空间内包括整个模型，整个计算域如图5 所示。

图5 整体计算域模型Fig. 5 The model of whole computational domain

对于流体部分，采用NULL 材料模型，搭配线性多项式状态方程描述流体变形与压力之间的关系，其中水的黏性系数设置为8.684×10−4(N·S)/m2，整个计算模型受到的重力加速度为9.8 m/s2。

采用侵蚀算法，即CONTACT_ERODING_SURFACE_TO_SURFACE 关键字处理船体结构与冰山之间的碰撞，设置CONSTRAINED_LAGRANGE_IN_SOLID 关键字用于处理结构和冰山与水之间的流固耦合。同时，为了避免冰山的结构网格与水域的网格之间重叠所带来的求解错误，INITIAL_VOLUME_FRACTION_GEOMETRY功能被用来进行流固耦合界面的初始化。

3.2 网格尺寸

根据LS-DYNA 软件理论指导手册的建议[19]，当流体域的网格尺寸与结构物的网格尺寸相近时，其流固耦合ALE 算法将有更理想的计算结果。因此，在对舷侧、冰山以及水域划分网格的过程中，同时考虑了计算精度以及计算效率的问题，船体结构采用Shell 单元建模，将舷侧肋板的网格尺寸定义为0.25 m，舷侧模型其他区域的网格尺寸定义为0.3 m。球形冰山采用Solid 单元建模，根据图3 所示的网格无关性结果，球形冰山的网格尺寸选择为0.15 m，水域和空气域的网格单元尺寸定义为0.3 m。计算模型各部分的网格类型以及对应的网格数量如表4 所示。

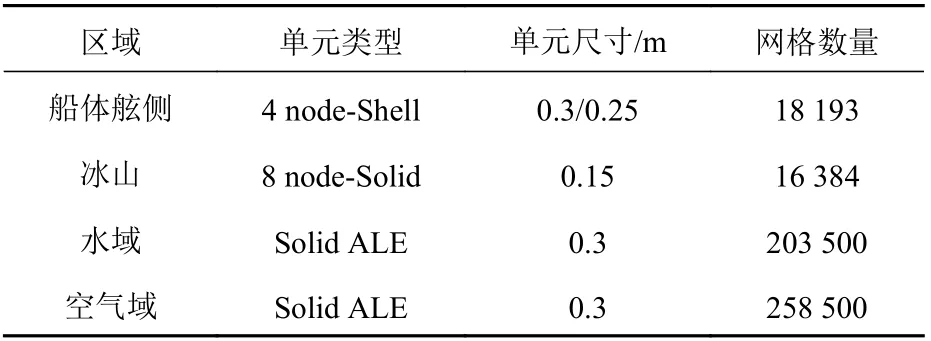
表4 模型网格参数Table 4 Parameters of the model mesh

3.3 模拟工况

在数值模拟中对舷侧边缘两侧进行刚性约束，使冰山以一定的速度和角度与舷侧碰撞。为了增加冰山运动过程中的稳定性，将浮冰z方向的自由度进行位移约束，其余方向自由运动。碰撞前，冰山距离舷侧法向的初始距离为1.5 m，以初速度V=5 m/s 向船舶运动。冰山与舷侧碰撞角度的俯视图如图6 所示。本文分别考虑了冰山与舷侧的碰撞角度α = 30°，45°，60°，75°和90°时的工况，模拟的物理时间为2 s。需要说明的是，本文所模拟的冰山撞击船舶与船舶撞击冰山在物理过程上略有不同，且未考虑船舶运动的影响，作为一种简化的处理手段[9,20-22]，模拟冰山撞击船舶可以更好地捕捉该过程中的流体阻滞效应和结构变形。

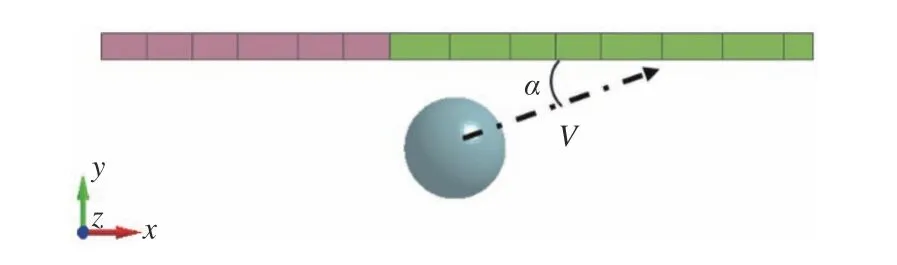
图6 碰撞角度俯视图Fig. 6 Top view of collision

4 结果及分析

选取舷侧与冰山的碰撞角度α = 60°的情况进行分析。图7 所示分别为数值模拟过程中在初始状态、0.45 s 以及1.21 s 不同时刻（T）舷侧与冰山的相对位置以及碰撞过程中的自由液面变化情况。由图可以看出，随着冰山的运动，自由液面变化剧烈，在冰山与舷侧结构之间逐渐兴起波浪，甚至导致舷侧上发生了波浪砰击，这与Song等[22]在模型试验中所观察到的现象类似。

图7 α = 60°时不同时刻舷侧−冰山碰撞现象Fig. 7 Collision phenomenon between side structure and iceberg with α = 60° at different times

4.1 碰撞速度分析

图8 所示为碰撞过程中冰山在3 个方向的速度改变曲线图。由图可以看出，垂直于舷侧方向的速度Vy由于受水的阻力以及波浪缓冲作用的影响，在碰撞发生前速度逐渐减小；在约0.51 s时，由于舷侧与冰山发生碰撞，Vy急剧减小，直至发生回弹；而平行于舷侧方向的速度Vx变化则比较缓慢，仅在碰撞时刻发生了小幅度的跳跃变化。与Vy相比，Vx在碰撞的瞬间更多地是受到摩擦力的影响，而Vy则是受到正面碰撞的影响，因此Vx的速度跳跃变化相对较小。此外，在碰撞前的速度衰减方面，Vy也更加明显。从图8 所示的自由液面变化中可以发现，舷侧法向的兴波更加剧烈，波浪缓冲影响更大，而Vx更多地是受到流体阻力的影响，变化不明显。

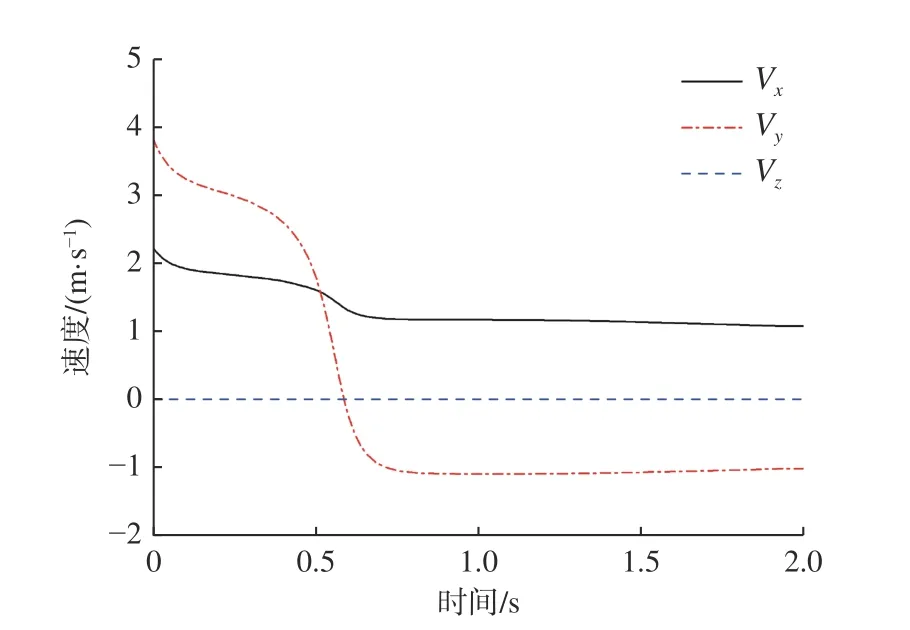
图8 α = 60°时的冰山速度变化情况Fig. 8 Velocity of iceberg with α = 60°

图9 所示为不同碰撞角度下，初始速度相同的冰山在碰撞过程中速度幅值随时间变化的情况。由图可以看到，随着碰撞角度的增大，冰山在接触法相方向上的速度分量随之增大，速度幅值的衰减越发明显。如上所述，在此过程（图7）中，碰撞角度越大，冰山和船体结构之间的法向兴波越剧烈，冰山因水动力的影响所受到的斥力作用也越明显，在斥力和阻力的共同作用下，速度也就会发生更快速的衰减。

图9 不同碰撞角度下的冰山速度幅值变化Fig. 9 Velocity amplitude of iceberg with different collision angles

4.2 应力分析

图10 所示为碰撞角度α = 90°时舷侧在不同时刻的等效应力图。在碰撞过程中，应力云图的面积逐渐增大，其中碰撞区域中心的应力最大，然后向周围逐渐变小；在碰撞接触最充分的时刻，应力云图的区域面积以及中心应力达到最大值，碰撞结束后，高应力区域面积随之减小。对应过程中的冰山应力云图如图11 所示，其与碰撞过程中舷侧的应力特征相似，即冰山碰撞区域中心的应力最大，周围的应力较小。同时，从图11(b)中可以看到，在垂直碰撞过程中，冰山发生了轻微的破碎现象。

图10 α = 90°时舷侧不同时刻的等效应力图Fig. 10 Equivalent stress contours of the side structure with α = 90° at different times

图11 垂直碰撞过程中不同时刻的冰山应力图Fig. 11 Stress contours of the iceberg at different times during vertical collision

4.3 不同碰撞角度下的碰撞力峰值

图12 所示为舷侧与冰山在不同碰撞角度下的碰撞力曲线。从图中可以看出，随着碰撞角度的增大，碰撞时刻不断提前。当α = 30°，45°，60°，75°时，碰撞力曲线的变化趋势相似，即在某一时刻碰撞力达到最大值后开始变小，碰撞力曲线光滑；且在这4 种碰撞角度下，均发生了冰山与舷侧碰撞的反弹过程，冰山未发生破坏。当α = 90°时，碰撞力发生了波动，其变化趋势与其他碰撞角度下的碰撞力曲线不同，原因是冰山在这种情况下发生了破碎，导致碰撞力出现波动现象。

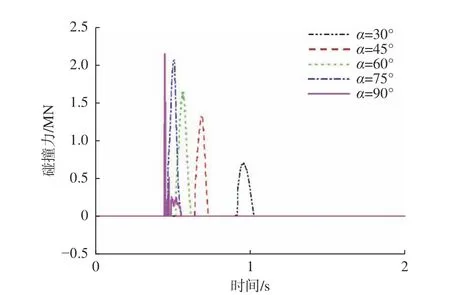
图12 不同工况下的碰撞力曲线Fig. 12 Curves of collision force in different cases

在图12 所示各种碰撞角度下的碰撞力曲线中，提取碰撞力峰值并绘制碰撞力峰值与碰撞角度的关系曲线图如图13 所示。由图中的曲线趋势可以看出，随着碰撞角度的增大，碰撞力峰值呈明显上升的趋势，在α = 30°～75°的阶段，碰撞力峰值上升明显，且增长幅度基本相同；在α = 75°～90°范围内，碰撞力稍有增长，增长幅度较小。其原因可能是当α = 30°，45°，60°，75°时，在碰撞的过程中冰山未发生破碎，而在α = 90°情况下冰山发生了局部破碎；另外，在α = 90°工况下，除碰撞过程中舷侧的塑性变形消耗能量外，一部分能量还被冰山破碎所消耗。

图13 不同碰撞角度下的碰撞力峰值Fig. 13 Peak collision force with different collision angles

4.4 船体结构的能量吸收

图14 给出了不同碰撞角度下船体结构的能量吸收情况。碰撞过程中，很大一部分能量被船壳的塑性拉伸所吸收，但在当前算例中，由于冰山的体积较小，在与船体结构发生碰撞时，船体结构并未发生明显破坏，碰撞结束后，船体板在发生一定的塑性变形后回弹，能量吸收曲线表现为迅速增加后略微下降。由图14（a）～图14（d）可以看到，舷侧外板为船体结构的主要能量吸收部件，且随着碰撞角度的增加，分配到舷侧外板上的能量越多。而当α = 90°时（图14（e）），由于在碰撞过程中冰山破碎带走了一部分能量，分配到船体结构上的碰撞能量明显下降，且除舷侧外板之外的其他构件也在能量吸收中占据有相当的比例。

图14 不同碰撞角度下船体结构的能量吸收Fig. 14 Energy absorption of ship structure at different collision angles

5 结 语

本文基于非线性有限元方法和ALE 算法建立了船舶舷侧结构与小型冰山相互作用的数值模型，并在模型中考虑了船舶结构变形、海冰破坏以及两者之间水动力的影响。其中，由海冰材料模型所得的压力−面积曲线与试验所得结果吻合较好，且整个数值模拟结果在现象上也与模型试验结果相似。然后，在上述基础上，研究了小型冰山以不同角度与舷侧结构发生碰撞时的过程中速度、碰撞力和船体结构能量吸收的变化。经分析发现，在冰山向舷侧运动的过程中，由于兴波消耗能量以及水的阻力作用，冰山的速度逐渐减小，冰山在以初速度运动撞击舷侧后发生了回弹；船舶舷侧结构的应力区域面积在碰撞过程中逐渐增加，应力由中心向四周逐渐减小，在碰撞接触最充分时产生了最大的中心应力和应力面积；随着舷侧与冰山碰撞角度的逐渐增大，碰撞力和船体吸收能量相应增加，但增幅不同，并且冰山是否发生破碎会影响到碰撞力和船体能量吸收的大小。

在下一步的工作中，计划引入船体的运动模型并开展船体防撞结构的优化设计。