厚松散层近浅埋煤层开采导水裂缝动态演化规律研究
赵兵朝,孙 浩,郭亚欣,杨 啸
(1.西安科技大学 能源学院,陕西 西安 710054;2.西安科技大学 教育部西部矿井开采及灾害防治重点实验室,陕西 西安 710054)
采动导水裂缝是造成生态水资源流失和矿井水害的直接原因。研究导水裂缝动态演化规律有助于深层次掌握裂缝发育机理和规律,对于实现保水开采以及防治矿井突水具有重要价值。对于采动导水裂缝发育规律,相关学者已取得较多成果:许家林等[1,2]基于关键层理论,将7~10倍煤层采厚作为关键层裂缝是否贯通的临界高度;高延法等[3]通过理论分析,将岩层中间层层向拉伸率超过临界拉伸率作为岩层破断的判断依据;赵兵朝等[4,5]研究了采动变形对岩层断裂损伤的作用,提出通过广义损伤因子判断裂缝发育;郭文兵等[6]分别对坚硬和软弱岩层的破断规律进行理论分析,得到导水裂缝带高度受关键层和软弱岩层破断距影响;余学义[7]、许延春[8]、滕永海[9]均通过对实测数据回归分析的方法,得出综采放顶煤条件下坚硬、中硬和软弱顶板导水裂缝带高度计算公式;刘辉等[10]通过地裂缝监测,提出采动地表临时裂缝表现为“增大—减小—闭合”的变化规律,裂缝深度和宽度存在线性正比例关系;张世青等[11]借助材料力学裂隙形成机理,发现岩层的挠度和跨距是裂缝形成的决定性因素;申玉三等[12]认为岩层层向拉伸率是分析岩层弯曲沉降程度和裂缝发育程度的关键指标;黄庆享[13,14]通过物理模拟和现场实测,认为隔水层的隔水性主要受“上行裂隙”和“下行裂隙”影响,建立了以隔采比为指标的隔水层隔水性判据。本文基于前人研究成果,通过理论分析、理论计算和相似模拟实验等方法,探究以下沉为关键参数的上行导水裂缝发育高度和以水平变形为关键参数的下行导水裂缝发育深度计算方法,借助概率积分预计理论对厚松散层近浅埋煤层开采导水裂缝动态演化规律展开研究。
1 岩土层导水裂缝发育规律
煤层开采导水裂缝主要由“上行裂缝”和“下行裂缝”组成[14]。采动覆岩受载荷及自重作用向采空区沉降,由于关键层对上覆(部分)岩层具有承载控制作用,上行导水裂缝发育主要受关键层位置影响。隔水土层具有抗压不抗拉的特性,由于采动造成的不均匀沉降,土层产生拉伸变形导致裂缝产生,临时裂缝随工作面推进趋于闭合,永久裂缝出现于采空区边界。
1.1 上行导水裂缝发育高度预计
根据关键层理论[15],在关键层发生破断下沉时,所控制的(部分)上覆岩层将发生同步下沉。因此可通过分析关键层的破断情况初步判断导水裂缝发育高度范围,判断方法如图1所示。通过钻孔柱状资料,计算判断主、亚关键层的位置,自下而上依次标记为关键层1~n。顺序判断各关键层的破断情况,若关键层1未发生破断,则导水裂缝带发育至关键层1底部岩层;若关键层1破断,则继续判断下一关键层,直至出现未破断关键层i,则裂缝发育至关键层i底部;若关键层均破断,则裂缝发育至基岩顶面,进而向土层发育。
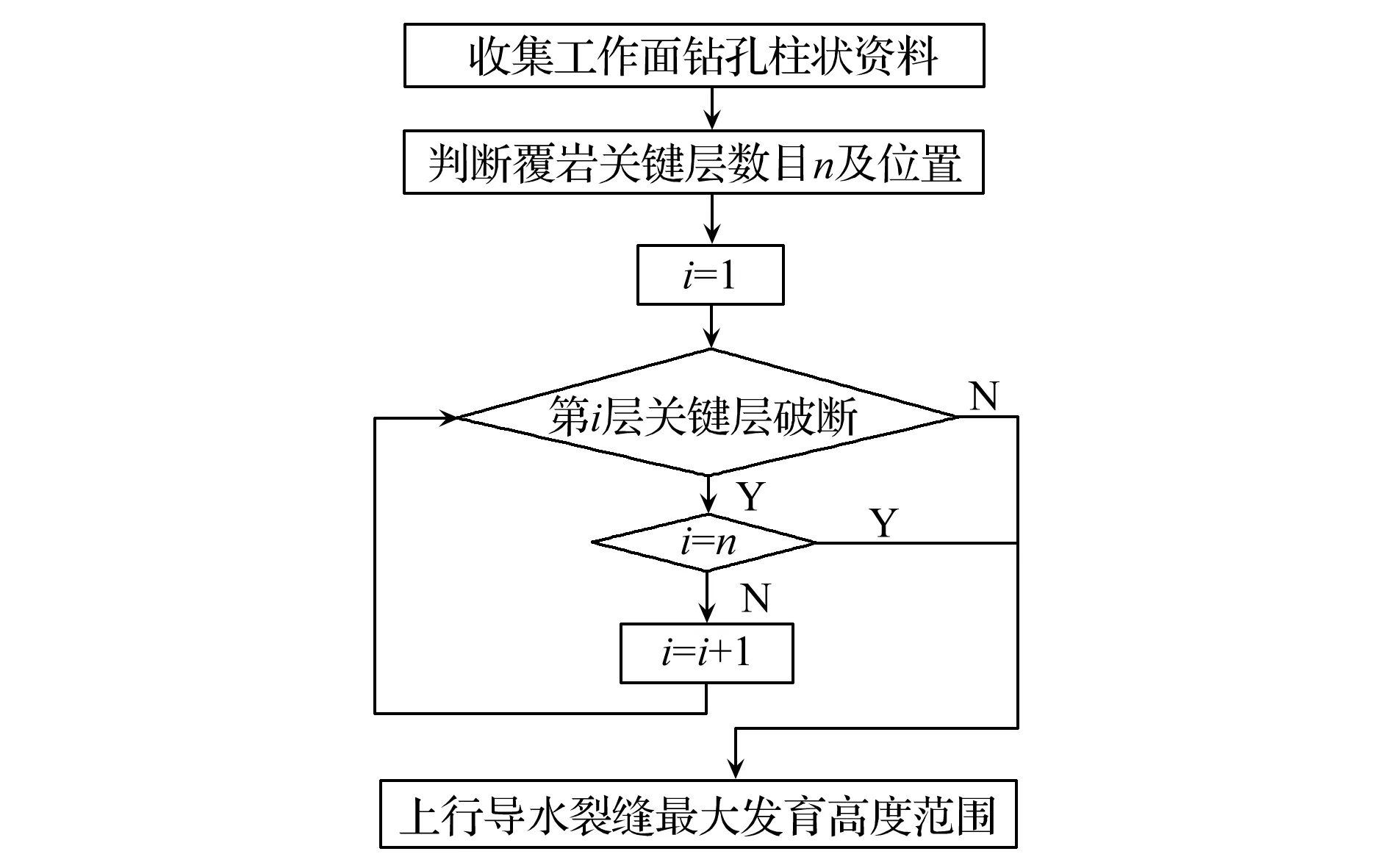
图1 上行导水裂缝发育高度范围判别流程
判断关键层是否发生破断可以通过分析关键层极限挠度与关键层下部最大自由空间的关系。当关键层极限挠度fmax小于关键层下部最大自由空间wmax时,岩层发生破断,裂缝继续向上发育,反之,裂缝停止发育,关键层及上覆岩层处于弯曲下沉带,见式(1)。
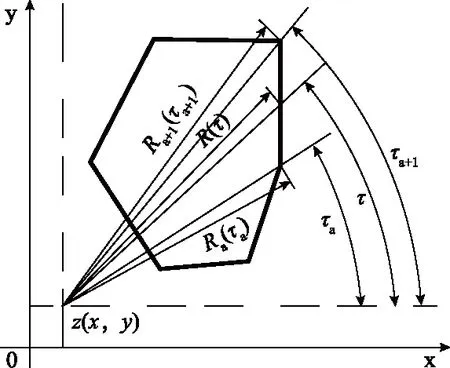
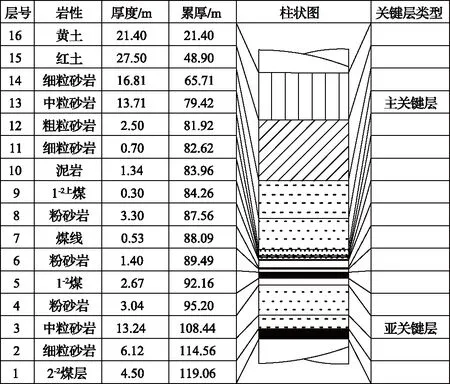
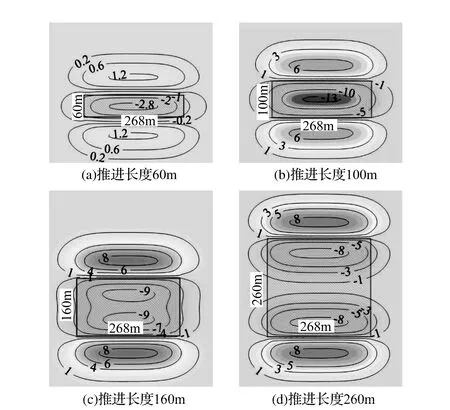
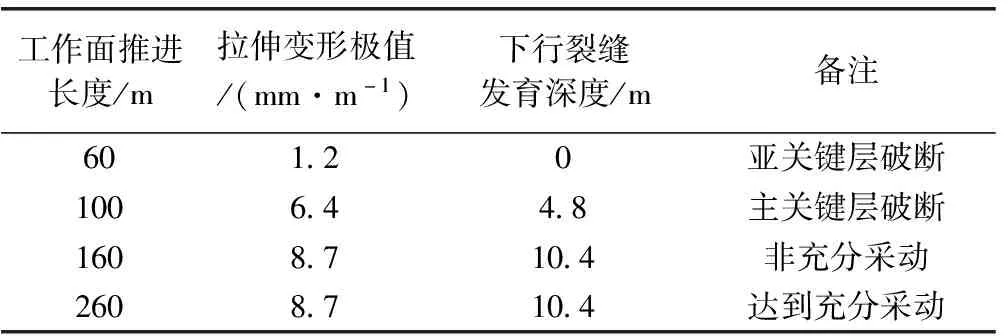
fmax fmax≥wmax,(关键层未破断) (1) 关键层极限挠度计算见式(2)。 (2) 式中,q为岩梁承受载荷,N/m2;l为岩梁长度,m;E为岩梁弹性模量,Pa;I为岩梁截面惯性矩,m4。 (3) 式中,bL为岩梁宽度,m;hL为岩梁厚度,m。 当上行裂缝发育突破主关键层,将贯穿基岩向土层发育,受厚松散层影响,上行裂缝发育高度需进一步判断[16]。前苏联学者格维尔茨曼[17]经大量实测得出全部跨落法开采时导水裂缝带顶部岩层极限曲率K与上行导水裂缝发育高度hs的关系,见式(4)。依此进一步预计裂缝高度。 (4) 式中,ηs为导水裂缝带顶部岩土层下沉系数;m为采厚,m;δ为岩层移动角,(°);φ为充分采动角,(°)。 由于主关键层控制上方岩土层随其同步运移,因此式(4)中参数ηs可取主关键层的下沉系数。导水裂缝带顶部岩层极限曲率K取值可通过格维尔茨曼拟合经验公式(5)计算得到[17]: K=0.4(eA/65+1) (5) 式中,A为导水裂缝带范围内黏土质岩与裂缝带高度的百分比,%。 开采造成的不均匀沉降导致隔水土层上表面产生拉伸变形,当拉伸变形达到土体的极限抗拉伸变形能力,隔水土层表面开始产生裂缝。基于土体破坏的极限平衡条件,将土层下行裂缝发育问题简化为平面应变问题,裂缝尖端微元体应符合如下本构关系[18]。 (6) 式中,εx、εz分别为x、z方向移动变形,mm/m;μ为泊松比;Et为土体变形模量,Pa;σx、σz分别为x、z方向有效应力,Pa。 土体的极限抗拉伸变形能力主要由土体黏聚力和上覆载荷造成的侧向水平应力决定。采动影响造成的应变松弛使土体侧向水平应力减小。当采动产生的拉应力足以克服土体黏聚力和侧向水平应力,隔水土层表面产生裂缝并向深处发育。土体产生裂缝的水平变形临界值ε0可通过式(7)计算[18]。 (7) 式中,c为土体黏聚力,Pa;φ为内摩擦角,(°)。 土体自重侧向应力随深度增大,在深度hm达到某一临界位置,采动附加应力恰好克服土体的黏聚力和土体自身侧向应力时,采动土体达到开裂临界状态,即深度hm以下土层不再发生开裂。将土体开裂临界状态应用于土骨架线弹性应力-应变关系式,见式(8)。 (8) 式中,σxm为采动附加水平应力,Pa;εxm为采动水平变形极值,mm/m。 σz=γ·hm (9) 式中,γ为土层的平均容重,kN/m3。 将σxm=-c及式(9),代入式(8)整理得: (10) 通过式(10)中可以得出下行裂缝发育深度hm与采动水平变形值εxm呈正相关,同时与土体本身性质密切相关。 由上述理论计算过程得出,上行裂缝发育高度预计基于关键层理论与岩土层下沉密切相关,下行裂缝发育深度以隔水土层采动水平变形为关键参数。为使裂缝发育预计结果更为准确,借助概率积分预计理论求取岩土层下沉和水平变形。 为获取煤层开采过程中上行裂缝发育高度和下行裂缝发育深度预计中的重要参数(关键层下沉和隔水层水平变形),采用概率积分移动变形预计理论展开分析。由于常规开采移动变形预计公式的研究对象是采动地表,与岩土层的移动变形有一定区别。因此基于地表移动变形预计相关研究成果[19-21],引用分析地表移动的相关参数,将影响半径r替换为r(z),移动角β替换为β(z),水平移动系数b替换为b(z),得到岩土层移动参数表达式,见式(11)—式(13)。 (11) (12) (13) 式中,z为岩土层所处深度,m;H为开采煤层埋深,m;r(z)为采动影响半径,m;β(z)为开采主要影响角,(°);b(z)为水平移动系数;n为主要影响半径指数,与岩层力学性质有关[19]。 为便于对不同形状开采单元的岩土层移动变形进行预计,将直角坐标系转化为极坐标系,建立预计模型,如图2所示。 图2 极坐标闭合积分 由以上模型得到式(14): (14) 式中,Ra为编号a的拐点极坐标半径,m;τ为直角坐标系中计算点和拐点连线与x轴间夹角,(°)。 基于上述极坐标模型,结合式(11)—式(14),并引入Knothe时间函数[22],得到采动上覆岩土层下沉值预计表达式,见式(15)。 (15) 式中,k为计算块段拐点数;Ci为下沉时间系数[19]。 Ci=1-esti (16) 式中,s为与岩层力学性质有关的影响系数;ti为开采时间系数。 (17) 式中,ε(x)为采动水平变形,mm/m。 基于式(15)得到的下沉预计式,结合式(17)得到采动上覆岩土层水平变形预计表达式,见式(18)。 (18) 基于上述模型和计算方法,可对煤层开采上覆岩土层动态下沉和水平变形展开预计。预计模型中主要参数包括地表最大下沉值ωmax、主要影响角正切值tanβ(z)和水平移动系数b(z)等,可参考相似地质条件工作面地表岩移监测结果进行取值。 以陕北地区韩家湾煤矿2304综采工作面为研究对象,该工作面煤层倾角2°~4°,为近水平煤层,煤层埋深125m,上覆基岩均厚65m,松散层均厚60m,其中萨拉乌苏组含水层均厚7m,部分出露于低谷地带,上覆风积沙层均厚5m,下伏离石组黄土和保德组红土,均厚分别约为21.4m和27.5m。工作面平均煤厚4.5m,工作面宽度268m,走向推进长度1800m,全部垮落法管理顶板,综合柱状图如图3所示。 图3 2304工作面综合柱状图 通过关键层理论判断得到工作面覆岩具有亚、主两层关键层,如图3所示。为判断关键层是否会受采动影响发生破断,首先对充分采动后(开采范围达到2倍煤层埋深)[19]关键层下沉进行预计,工作面宽度268m,取推进距离300m。预计所需参数参照相邻工作面地表岩移监测结果:下沉系数η=0.56,移动角正切tanβ=1.97,水平移动系数b=0.31,预计得到亚、主关键层下沉盆地等值线,如图4所示。由图4可知,开采达到充分采动后,亚关键层预计最大下沉值3105mm,下沉系数0.69;主关键层预计最大下沉值2520mm,下沉系数0.56。 图4 充分采动后关键层下沉等值线(mm) 分别计算亚、主关键层的极限挠度和预计最大下沉作比较。亚关键层承受载荷q1=99.4×103kPa,岩梁长度l1=272m,弹性模量E1=4.5MPa,岩梁宽度和厚度bL1、hL1为13.24m,上述参数代入式(2)、式(3)得到亚关键层岩梁极限挠度fmax1=1.23m。主关键层承受载荷q2=430.6×103kPa,岩梁长度l2=291m,弹性模量E2=4.5MPa,bL2、hL2为13.71m,上述参数代入式(2)、式(3)得到主关键层岩梁极限挠度fmax2=1.73m。结合图4可知,达到充分采动后,亚、主关键层预计最大下沉值均大于极限挠度,即亚、主关键层均会随工作面推进发生破断。 结合式(1)可知,亚关键层下沉ω1达到1.23m时发生破断;主关键层下沉ω2达到1.73m时发生破断。通过预计模型反算得到亚、主关键层破断对应工作面推进长度分别为54m和93m,下沉等值线如图5所示。 图5 关键层破断时下沉等值线(mm) 由上述可得,工作面推进至54m,亚关键层发生破断,上行裂缝发育至主关键层底部,高度为35.1m(7.8倍采高)。工作面推进至93m,主关键层发生破断,裂缝继续向上发育。通过式(4)可进一步预计裂缝最大发育高度。基岩层中,黏土质岩共厚1.34m,即A值应为0.02,代入式(5)得到岩层极限曲率K=0.8×10-3/m。将相关参数代入式(4)计算得到上行导水裂缝预计最大发育高度hs=82.8m(18.4倍采高)。 2304工作面隔水层均厚48.9m,隔水层顶面距煤层114.6m。通过岩土层动态移动变形预计模型,预计得到从未充分采动到充分采动过程中隔水层水平变形分布等值线,如图6所示。由图6可知,随工作面开采推进长度增大,地表水平变形(工作面推进方向)逐渐增大直至达到充分采动。水平变形关于采空区推进方向中线对称分布,水平变形极值始终位于采空区边界两侧,煤柱侧为拉伸变形,采空区侧为压缩变形。当工作面推进至60m时,亚关键层初破断,隔水层处于非充分采动,出现3处水平变形极值,最大拉伸变形值达到1.2mm/m,如图6(a)所示;工作面继续推进至100m,主关键层已破断,最大拉伸变形值达到6.4mm/m,如图6(b)所示;随工作面继续推进,拉伸变形增大并逐渐稳定达到极值8.7mm/m,压缩变形极值逐渐减小,地表开始出现4处水平变形极值,如图6(c)所示;当工作面开采达到充分采动,水平变形值稳定,拉伸、压缩变形极值为±8.7mm/m,如图6(d)所示。 图6 隔水层水平变形等值线(mm/m) 基于上述水平变形变化预计,计算相应下行裂缝发育深度。土体参数泊松比为0.35、容重1.607×104N/m3、弹性模量18.5MPa、内摩擦角32°、黏聚力93.8kPa,将上述参数与不同推进距离下拉伸变形极值代入式(7)、式(10)得到隔水层产生下行裂缝的临界水平拉伸变形值为3.4mm/m,即水平拉伸变形值小于3.4mm/m时不会产生下行裂缝,下行裂缝发育深度预计见表1。由表1可得,随工作面推进,亚、主关键层依次破断,采动水平拉伸变形极值与下行裂缝发育深度随之增大。当工作面推进达到充分采动后,下行裂缝发育深度达到极值为10.4m。 表1 下行导水裂缝发育深度预计 为验证导水裂缝动态演化规律,以2304工作面为原型,搭建相似模拟实验模型,模型相似比为1∶150,尺寸为2850mm×1200mm×200mm,煤层采高4.5m。 模拟工作面推进过程中,由于亚关键层对上覆部分岩层具有控制作用,工作面推进至67.5m时,亚关键层发生破断,上覆部分岩层同步弯曲下沉,主关键层下方出现明显离层,裂缝发育至主关键层底部,发育高度为48.9m,如图7所示。 图7 亚关键层破断后裂缝发育形态 工作面推进至105m时,主关键层发生破断,上覆岩土层同步下沉,裂缝贯穿基岩层,由于土层具有抑制裂缝发育的作用,裂缝未能贯穿土层,发育高度为77.2m。同时,隔水层表面出现下行裂缝,位于采空区边界外侧,发育深度为4.2m,如图8所示。 图8 主关键层破断后导水裂缝发育形态 相似模拟实验煤层开采260m,已达到充分采动,上行裂缝最终发育高度为86.3m,采空区中部下行裂缝随工作面推进趋于闭合,边界下行裂缝发育显著,达到9.7m,如图9所示。 图9 开采结束裂缝最终发育形态 相似模拟实验现象与裂缝动态发育预计结果基本相符,验证了导水裂缝动态演化规律的可靠性。 1)基于关键层理论,得出以关键层下沉和极限挠度为主要参数的上行导水裂缝高度计算方法;结合非饱和土力学与开采沉陷理论,推导出以隔水层水平变形为主要参数的下行裂缝发育深度预计公式。 2)通过调整地表开采沉陷预计理论中的概率积分参数,得出极坐标系下的岩土层全盆地移动变形预计模型,给出了煤层开采岩土层动态下沉和水平变形预计公式。 3)研究预计陕北某矿2304工作面推进过程导水裂缝动态变化,相似模拟实验现象与预计结果基本相符,验证了预计方法的可靠性。1.2 下行导水裂缝发育深度预计
2 岩土层动态移动变形预计模型
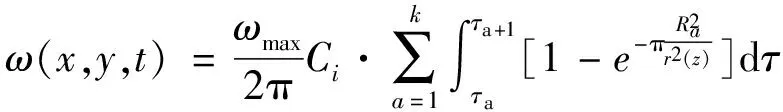
3 导水裂缝发育形态动态预计
3.1 工作面概况
3.2 基于关键层下沉的上行裂缝动态预计


3.3 基于隔水层水平变形的下行裂缝动态预计
4 相似模拟实验验证



5 结 论

