安家岭露天煤矿过背斜开采方案优化及比选
赵红泽,刘元旭,郭 帅,杜海瑞,邵志奔,林泽辰
(1.中国矿业大学(北京 能源与矿业学院,北京 100083;2.深部岩土力学与地下工程国家重点实验室,北京 100083;3.中煤平朔集团有限公司,山西 朔州 036800)
矿产资源的开发利用是推动我国经济发展的因素之一,在矿山的开采过程中,露天采矿是其中主要的开采方式[1]。随着资源的不断开发利用,原来的露天开采场地地质条件逐渐进入复杂阶段[2]。安家岭露天矿在近几年生产过程中遇到了大范围逆断层、背斜等地质构造,尤其东部的芦子沟背斜东翼地层倾角较陡(15°~25°),不仅对露天矿生产造成了严重的影响,还对开采程序的优化提出了更高的要求[3-5]。
针对复杂地质条件下开采程序的优化国内外有许多优秀研究成果可供借鉴,国内的张瑞新等人以系统工程理论为指导,结合露天矿中实际生产问题,提出了递阶优化的方法,即通过分范围、分目标、逐步深入的方法实现露天矿开采程序的优化[6];王韶辉、才庆祥等人以新疆天池能源南露天煤矿为例,结合煤层赋存条件、生产剥采比、综合运距等因素,提出了四种开采转向方案并进行对比分析,得出了最优方案,缩短了采区转向过渡时间,为企业创造了显著的经济效益[7];国外的O Litvin,M Tyulenev等人则针对露天矿在构造扰动带情况下开采时煤损的计算方法,提出断层错位区域反铲挖掘采煤损失计算的模型以及错位区煤层开采的技术方案[8]。本文在找出技术、经济可行的背斜区域生产开采方案基础上,为露天煤矿实际生产提供一定的理论支持和决策依据。
1 安家岭露天矿基本概况
目前安家岭露天煤矿已经进入芦子沟背斜区域,由于背斜构造的影响,露天矿坑底下部煤层倾角急剧增大,平均倾角达到8°~12°,局部最大倾角22°,煤层落差达到270m以上,地表和基岩面下降50~100m,首采区坡度分布及底板等值线如图1所示。其中F12断层以北降深速度尤为明显,对于一直以近水平推进方式开采的安家岭露天矿,煤层急剧下降会导致排土运距增加、内排空间不足、连续生产难度加大、设备无法高效安全作业等一系列开采方面的问题[9],因此相应的开采程序需要在开采现状的基础上随之做出优化调整。

图1 首采区坡度分布及11煤底板等值线
2 开采程序优化方案研究
2.1 现采区工作线直推方案
安家岭露天矿目前采区工作线大致沿南北方向布置,最下层11煤工作线约为1400m,该方案在此基础上工作线由西向东推进,随着边界的变化做实时调整,直推到界。其优点是可以按照现有开采程序不变,长工作线生产有利于大型设备能力的发挥,容易达到核定产能产量要求;缺点是长工作线推进,推进速度缓慢,背斜区域需要较长时间才能度过,会造成排土空间不足的问题。现采区工作线直推方案如图2所示。
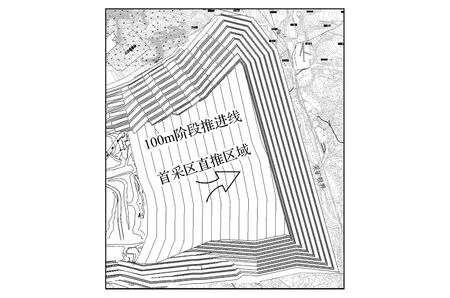
图2 现采区工作线直推方案
2.2 “直推+北部超前”方案
为快速度过背斜区域同时考虑到北部区域的F12逆断层,提出了“直推+北部超前”方案,以11煤F12断层为界,迅速在北部超前推进,度过背斜影响区,实现反向内排,而南部作为北部产量不足的弥补,缓慢推进,以4煤工作线为界逐步靠帮。北部强推到界后,实现转向横采,采煤工作面沿断层走向,从而避免了断层对采煤影响。“直推+北部超前”方案如图3所示。
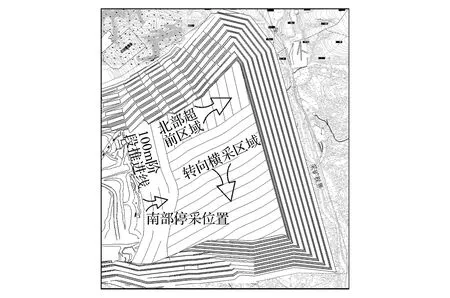
图3 “直推+北部超前”方案
2.3 “L”型扇形转向方案
针对直推方案所存在的不足进行优化,提出整体直推下的“L型”扇形转向方案,即在南部工作线以某一点为圆心,呈扇形推进并逐渐旋转,在北部直推开采到平缓地带即将到界时完成转向,最终形成近似于“L型”的横采工作线,从而在首采区结束后向南直推到二采区。“L”型扇形转向方案如图4所示。
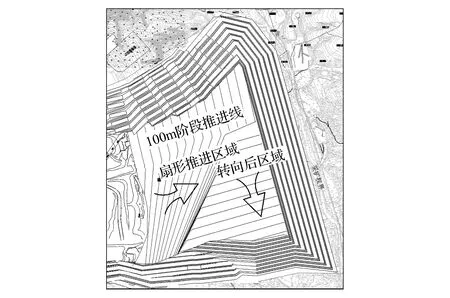
图4 “L”型扇形转向方案
3 基于AHP-TOPSIS法的方案评价
目前关于解决露天矿程序优化问题的分析方法主要有动态规划法、层次分析法、TOPSIS法及灰色关联法等[10]。
层次分析法(AHP法)是指将与决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。此法所需定量数据信息较少,且在每个层次中的每个因素对结果的影响程度都是量化的,非常清晰明确,容易为决策者了解和掌握;但此法只能从备选方案中选择较优者,不能为决策提供新方案,且指标过多时,数据统计量大,且权重难以确定[11];
TOPSIS法,又称优劣解距离法,是根据有限个评价对象与理想化目标的接近程度进行排序并在现有的对象中进行相对优劣的评价的方法。该方法对数据分布及样本含量没有严格限制,数据计算简单易行[12]。
本文将层次分析法和TOPSIS法相结合,用AHP法得出不同方案下指标合理权重,再用TOPSIS法,建立一个基于AHP-TOPSIS法的综合评价模型,确定最优的开采程序方案[13]。
3.1 构建层次分析结构模型
根据对上述各方案的分析,选取生产成本、综合运输功、生产能力、综合运距、生产均衡剥采比、新增排土空间、背斜过渡时间、开采难易程度以及构造复杂程度这九个指标来构建三个方案的评价指标体系,利用层次分析法进行综合比选[14],层次结构模型如图5所示。

图5 开采程序优化层次结构模型
3.2 AHP-TOPSIS法评价模型
3.2.1 根据评价指标构建规范化决策矩阵
先建立决策矩阵:
X=(xij)m×n
再构造规范化决策矩阵:
Y=(yij)m×n
文中所用指标存在极大、极小两种类型:
对于极大型指标,令:
(1)
对于极小型指标,令:
(2)
式中,xij为方案i的评估指标j的样本数据;yij为规范化后的xij值。
根据上述公式构造规范矩阵,其中极大型指标的数值越大,则方案越优;极小型指标的数值越小,则方案越优。
3.2.2 构建判别矩阵
采用一致性矩阵,将相同层元素两两进行比较,而不是采取同层共同比较,通过1—9级标度来构造判断矩阵。bij(i,j=1,2,3,…,n)表示的是第i个元素相对于第j个元素的比较结果,以1—9级标度及其倒数来具体取值,表示方法见表1。

表1 判断矩阵标度定义
由上述标度得到初始判别矩阵:
B=(bij)n×n
式中,bij为矩阵B的第i行,第j列元素;n为矩阵阶数。
3.2.3 指标权重计算及一致性检验
考虑到一致性的偏离可能是由于随机原因造成的,因此在检验判断矩阵是否具有满意的一致性时,还需将CI和随机一致性指标RI进行比较,得出检验系数CR,公式如下:
(3)
(4)
式中,λmax为判断矩阵最大特征值;n为判断矩阵阶数;CI为一致性检验指标;RI为平均随机一致性指标(其不同阶数下的取值见表2)。

表2 平均随机一致性指标
当CR<0.1时,则认为该判断矩阵通过一致性检验,否则就必须调整判断矩阵,直到具有满意的一致性为止。
3.2.4 构造加权规范化矩阵
运用层次分析法确定各评判指标权重为:
W=(W1,W2,…,Wn)T
则有:
zij=Wj·yij(i=1,2,…,m;j=1,2,…,n)
(5)
3.2.5 确定正、负理想解Z*和Z0
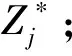
(6)
(7)
3.2.6 计算距离及相对接近度
(8)
(9)
计算评估对象对应点到正理想点的相对接近度:
(10)
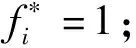
3.3 开采程序方案综合评价
由上述评价模型对三种优化方案进行评估,各方案的评价指标采用原始数据,其中“C8”和“C9”两个指标由施工人员现场判断:“难”“复杂”取值9;“较难”“较复杂”取值6;“一般”取值4;“容易”“不复杂”取值2,数据见表3。

表3 各方案评价指标原始数据
将表3中数据按照式(1)和式(2)进行归一化处理,得到结果见表4。
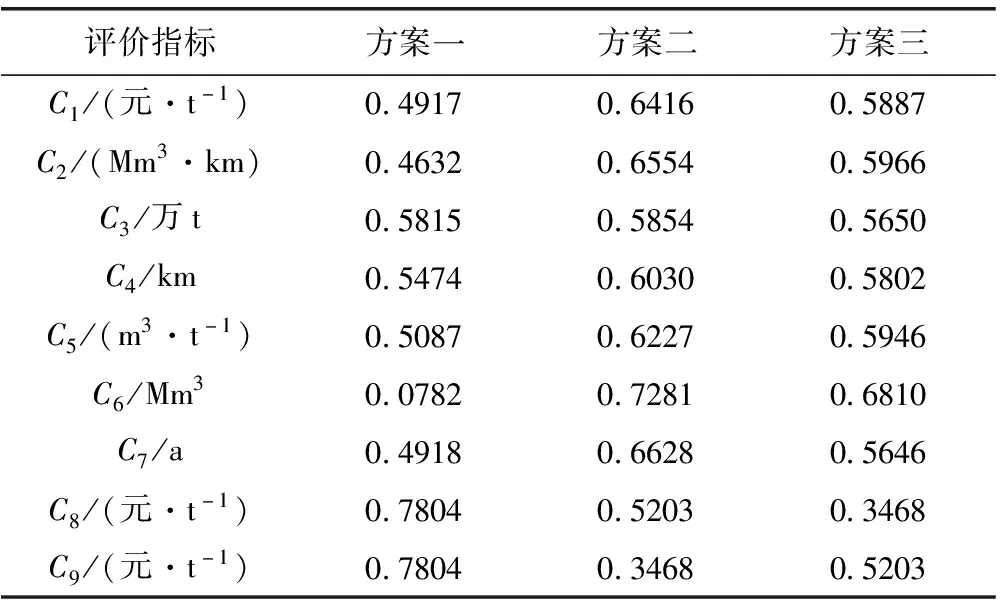
表4 各方案评价指标归一化后数据
根据层次分析法基本原理对结构模型中各因素按照1—9的比例标度法进行两两比较,得到表5的判断矩阵,并且利用软件Matlab计算各判别矩阵的最大特征值和其对应的归一化向量,然后利用式(3)和式(4)计算CR值用于一致性检验,最终确定权重结果,见表5—表8。
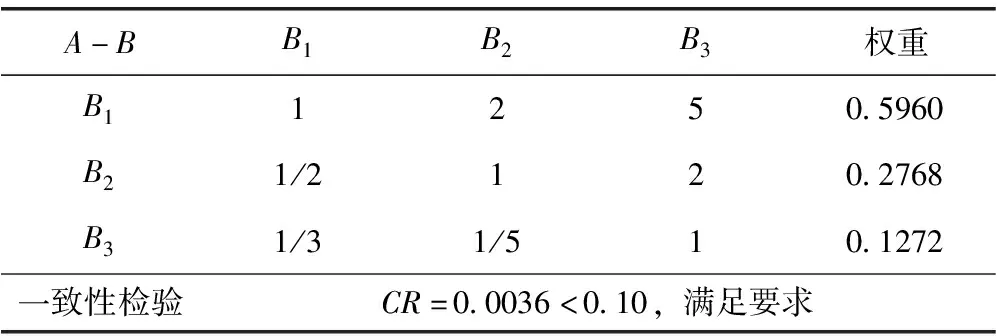
表5 A-B判断矩阵
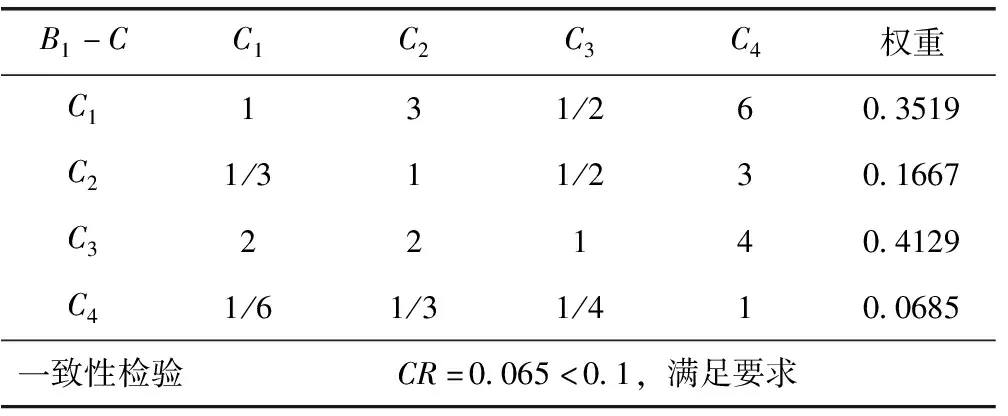
表6 B1-C判断矩阵

表7 B2-C判断矩阵
经过总排序计算,得到各评价指标权重见表9。

表9 评价指标权重表
由式(5)对规范化后的指标进行赋权重,结果见表10。
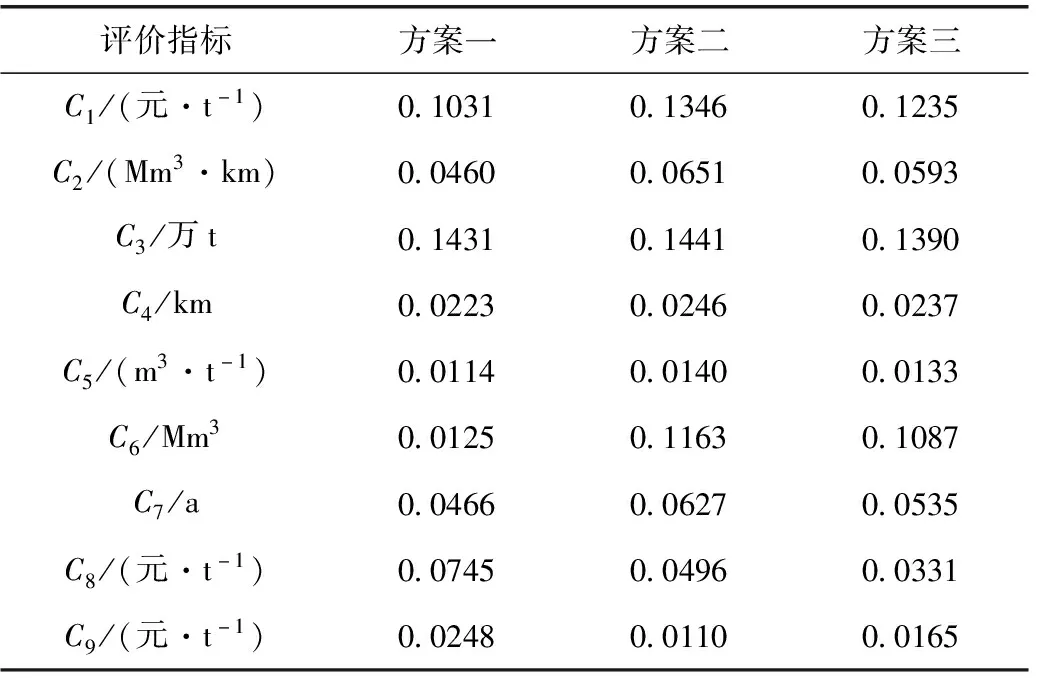
表10 各方案指标赋权重
根据式(6)和式(7)计算出正理想解、负理想解,见表11。

表11 各评价指标正、负理想解值
由式(8)、式(9)、式(10)计算得到各方案与正负理想解之间的距离、贴近度以及排名,见表12。
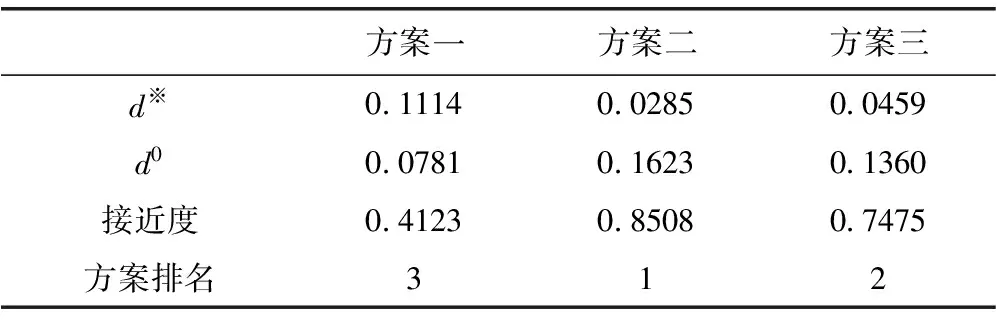
表12 各方案与正、负理想解的距离及贴近度
由上述评价可知,“直推+北部超前”方案为最佳开采程序方案。
4 结 论
1)在露天矿推进度、降深速度和年产量的约束下,通过对背斜区煤层底板赋存规律、开采境界空间形态及生产现状进行综合分析,提出了三种基本可行的开采程序方案,分别为现采区直推方案、“直推+北部超前”方案和“L”型扇形转向方案。
2)运用AHP法对所确定的9个评价指标建立层次分析结构模型,并计算出各指标满足一致性检验的合理权重值,其中吨煤生产成本、生产能力和新增内排空间三个指标所占权重较大,其余指标权重均小于0.1。
3)基于AHP-TOPSIS法评价模型,对三种开采程序方案主要的技术、经济指标进行计算分析之后,得出各方案与正负理想解之间的距离及贴近度,最终确定“直推+北部超前”方案为最优方案。

