可拉伸的ARAP++曲面参数化算法

王钊，邵春芳，孔闪闪，宿婧，张洁琳

(1. 华北理工大学 理学院，河北 唐山 063210；2. 大连科技学院 基础部，辽宁 大连 116052；3. 吉林大学 数学学院，吉林 长春 130012)

引言

近年来, 曲面参数化是计算机图形学领域备受关注的研究热点。它在计算机辅助设计和数字几何处理等相关方向有着广泛的应用。该项研究提出了可拉伸的ARAP++曲面参数化算法, 这是一种新的局部/全局参数化方法。主要受到平面参数化方法[1-3]和球面参数化方法[4-6]的启发, 首先通过ARAP++方法优化原始网格的Spring能量[7], 然后通过调整Jacobian矩阵奇异值的指数, 来控制曲面参数化效果的拉伸形变, 从而得到一系列有效的参数化结果。数值实验结果表明, 该算法与经典参数化算法相比, 在角度、面积、拉伸扭曲和运行时间方面都具有一定的优势, 并且得到了较好的纹理映射效果, 如图1所示, 其中θ表示拉伸因子。

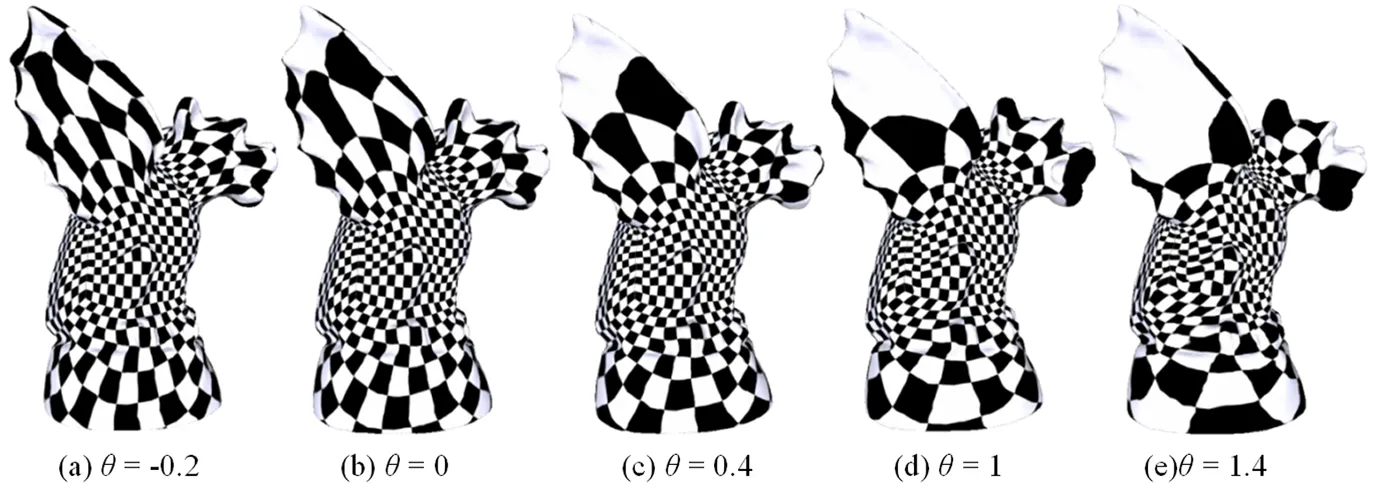
图1 Gargoyle模型纹理映射效果

该研究创新点如下, 基于ARAP++方法提出了一种可拉伸的曲面参数化方法, 该方法可针对含边界的三角网格模型得到固定边界和自由边界的可拉伸的曲面参数化结果,也可针对零亏格的三角网格得到可拉伸的球面参数化结果。该方法建立了局部全局参数化算法的从平面区域到球面区域的桥梁, 也实现了从共形参数化到等距参数化的渐变过渡, 能够更好地处理高曲率模型的参数化。

1相关工作

主要介绍与该算法紧密相关的方法和扭曲度量，以便于更好地阐述该算法和实验。

1.1 平面ARAP++方法

设S是原始网格,pi是S的网格点,pj是pi的一环点。S*是参数化网格,qi是S*的网格点,qj是qi的一环点。根据局部Spring能量[7]表达式：

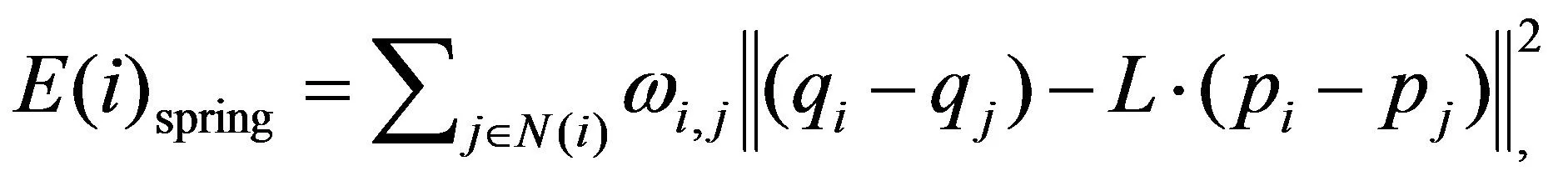
(1)

通过优化整个网格的Spring能量, 可以得到平面ARAP++方法[2]

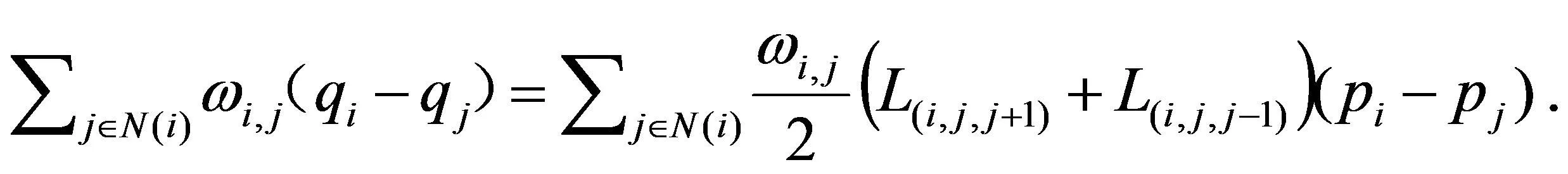
(2)

其中ω可以选择5种经典权值, Uniform权值, Cotan权值[8], Shape-preserving权值[9], Intrinsic权值[10], Mean-value权值[11], 该权值ω为Mean-value权值,L表示拟合矩阵[5]。

1.2 球面ARAP++方法

设S是原始网格,pi是S的网格点,pj是pi的一环点。S*是参数化网格,qi是S*的网格点,qj是qi的一环点。通过优化整个网格的Spring能量, 可以得到球面ARAP++方法[2]

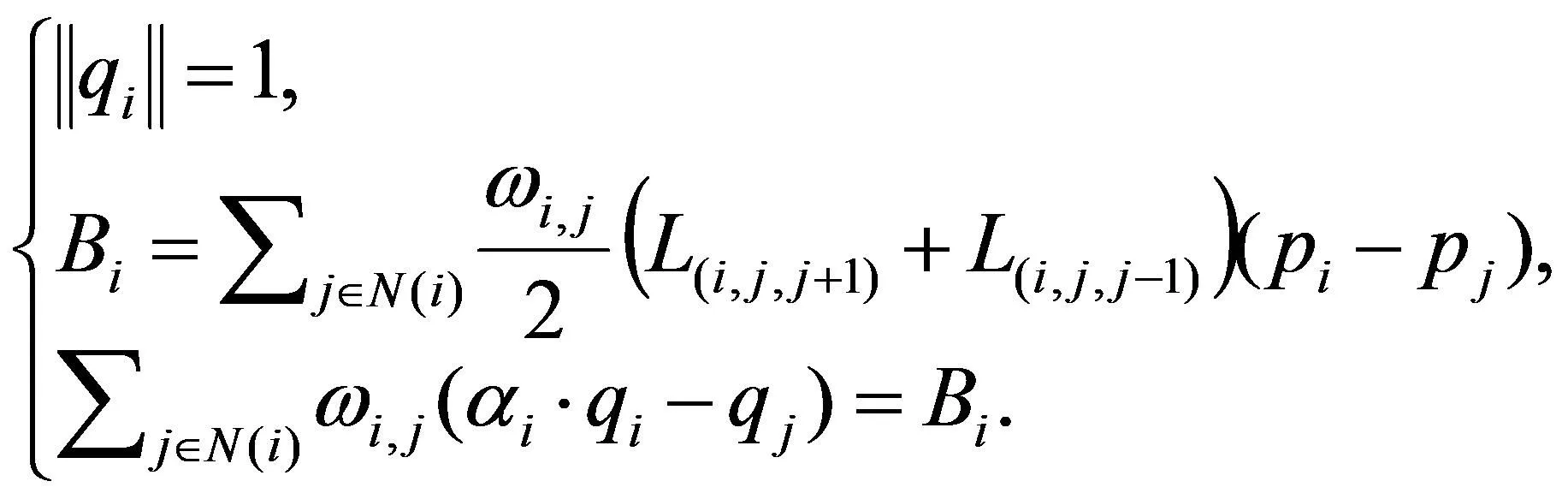
(3)

其中α是辅助变量,qi=(xi,yi,zi),Bi=(ai,bi,ci),上面的(3)式可以化简为

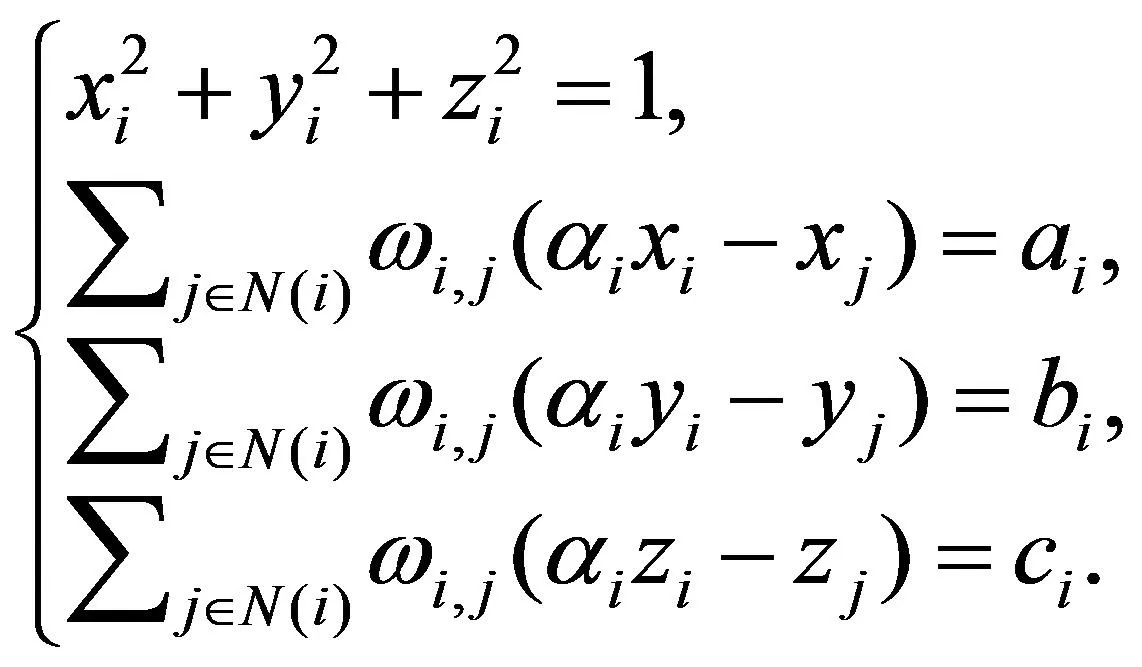
(4)

可以采用牛顿法求解(4)式, 得到球面参数化结果。

1.3 拟合矩阵的计算

拟合矩阵L是由原始网格S中的Δp1p2p3和参数化网格S*中对应的Δq1q2q3来计算，设

(5)

经过文献[5]中的推导, 可以得到

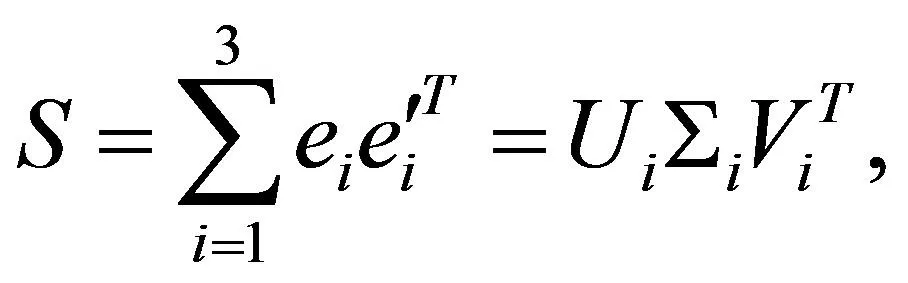
(6)

(7)

其中旋转矩阵R和2个拟合矩阵L(等距矩阵，共形矩阵)分别为：

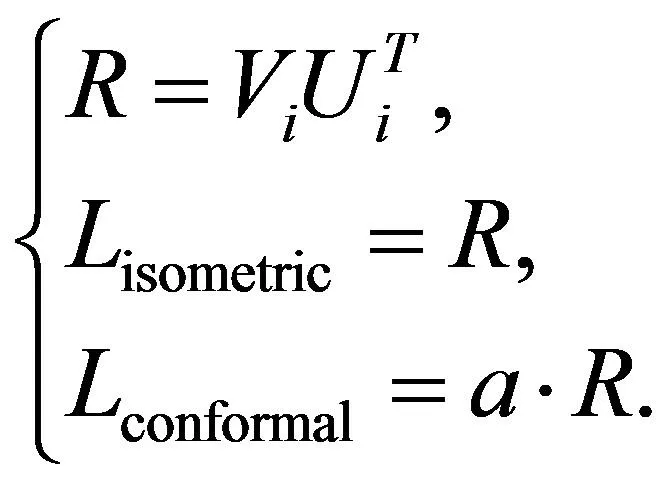
(8)

1.4 参数化的扭曲度量

设S和S*分别表示原始网格和参数化网格,θ和φ分别表示S和S*中三角面片的角度,F表示面片的数量,A(T)表示三角形T的面积。则在参数化比较中, 角度和面积扭曲分别为：

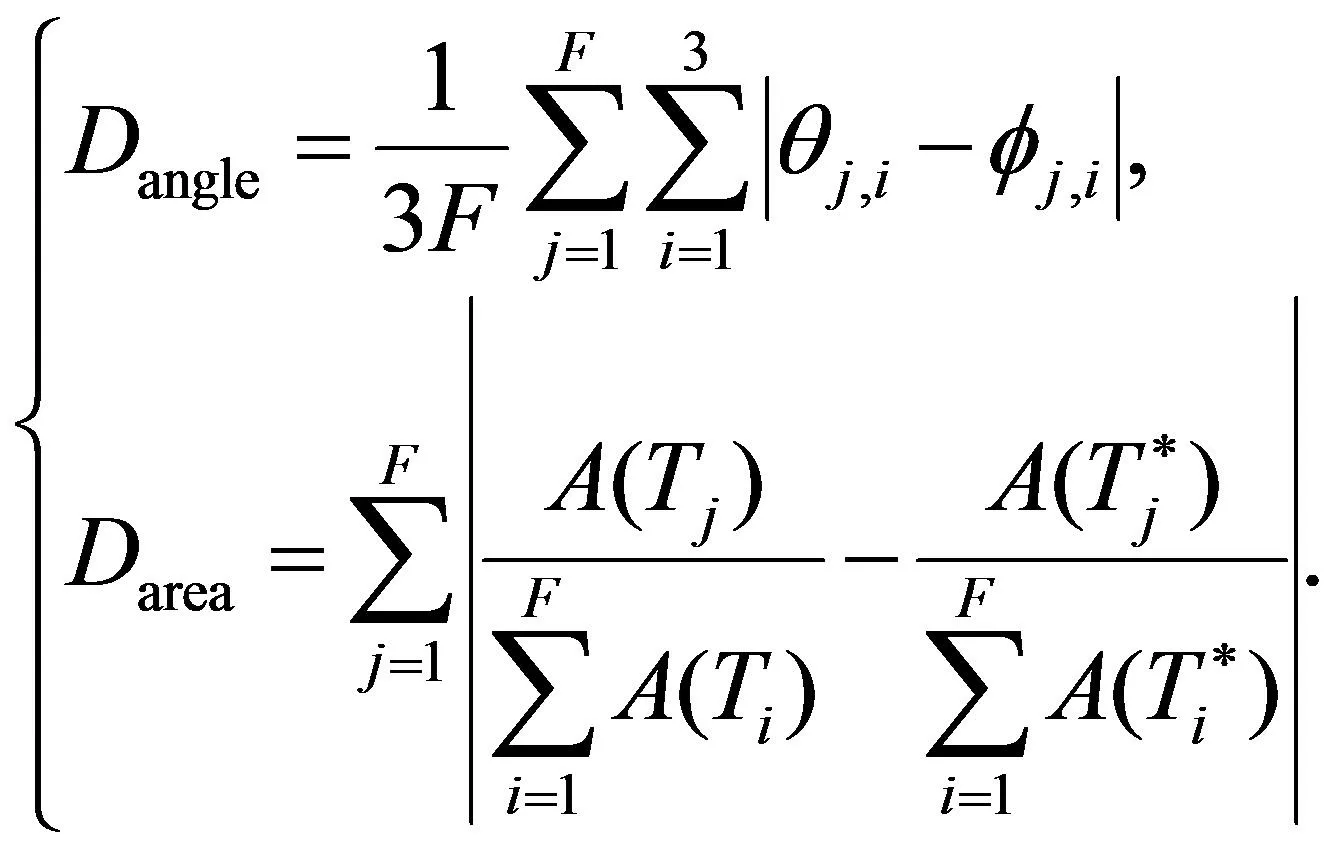
(9)

拉伸扭曲[14]通过三角形的Jacobian矩阵计算,Γ和γ分别是该矩阵的最大和最小奇异值。

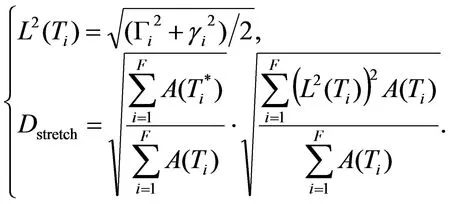
(10)

2曲面参数化算法

该项研究提出了可拉伸的ARAP++的曲面参数化算法, 它是一种渐变的的局部/全局参数化方法, 可以得到3类可拉伸的参数化结果, 分别是平面固定边界, 平面自由边界和球面上的参数化结果。作为该算法的基础, 读者可以参考相关文献[1-6]。

2.1 可拉伸的ARAP++曲面参数化算法

该算法为平面ARAP++方法和球面ARAP++方法的改进, 整体框架与ARAP++方法保持一致, 其核心部分为通过调整拟合矩阵奇异值的拉伸指数, 来得到可拉伸的参数化结果。

首先利用(6)式和(7)式, 可以得到共形矩阵和等距矩阵, 分别表示为：

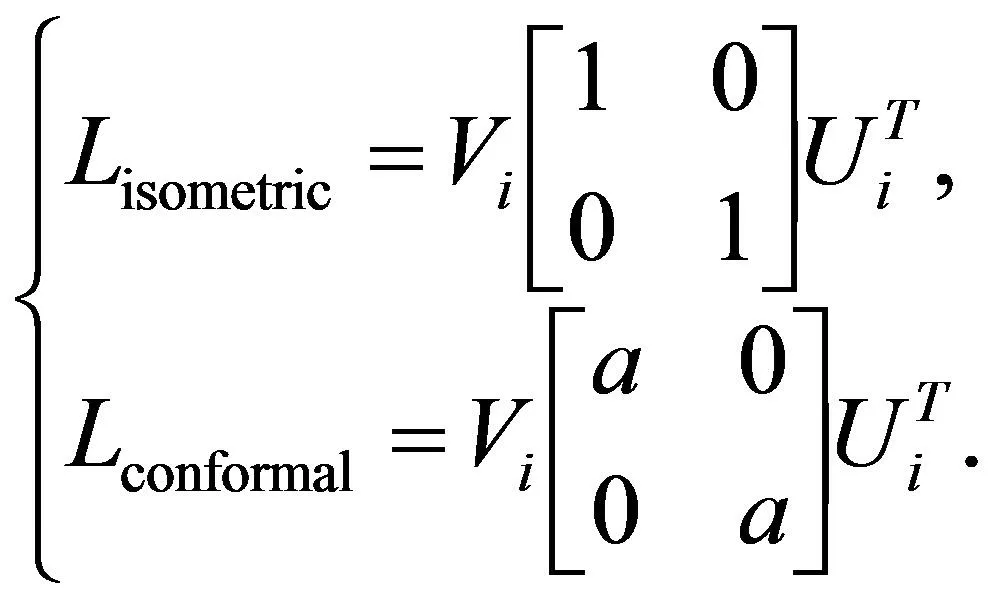
(11)

然后对拟合矩阵做变形,θ称为拉伸指数, 它的取值范围一般为[-2, 2]。当θ等于0时,Lstretch与Lisometric相等, 当θ等于1时,Lstretch与Lconformal相等。可得拉伸矩阵为：

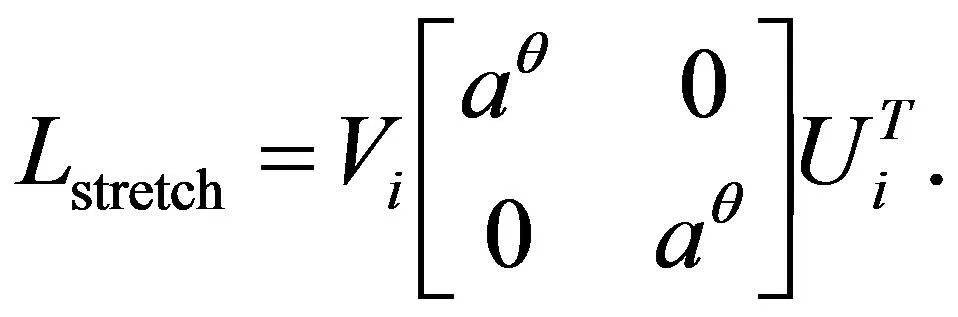
(12)

最后将拉伸矩阵Lstretch代入到(2)式中, 计算求解。该研究中对于每个θ值, 在全局求解时, 只需要计算一次, 不需要迭代。

在球面参数化的计算中, 首先将Lstretch推广至三维空间, 然后将Lstretch代入到(3)式和(4)式进行化简, 最后利用牛顿迭代法进行求解。

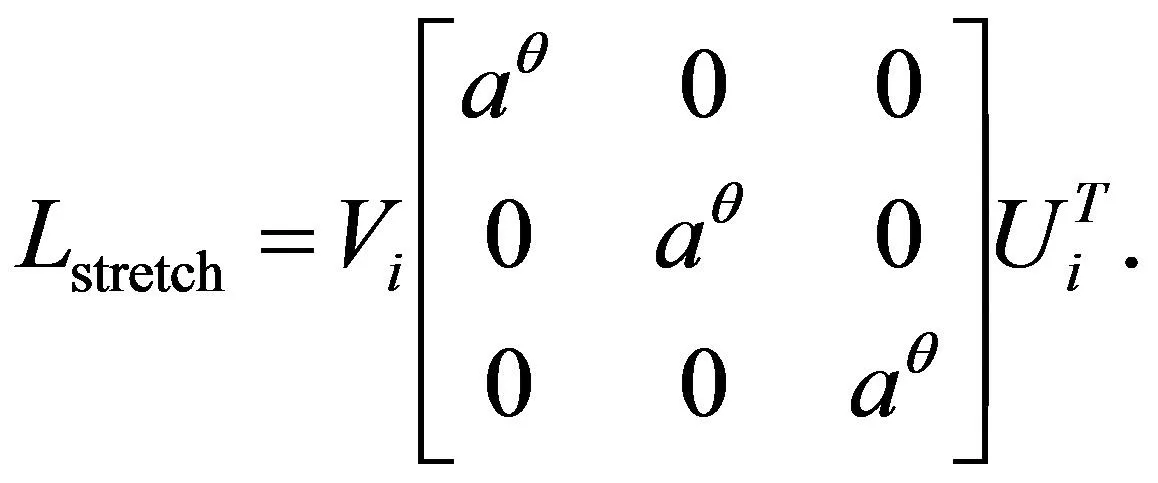
(13)

2.2 曲面参数化的展示

该算法既可以应用于平面参数化的计算, 也可以应用于球面参数化的计算, 对于平面参数化的计算分成2种情况, 如图2所示, 固定边界的平面参数化。如图3所示, 自由边界的平面参数化。在平面ARAP++方法的求解过程中, 可以只固定1个顶点在平面上, 经过全局求解后, 便得到自由边界的参数化结果, 也可以将所有的边界点固定到圆形或者正方形上, 然后全局求解, 便得到固定边界的参数化结果。

图2 Bumpy模型: 不同拉伸指数对应的固定边界的平面参数化

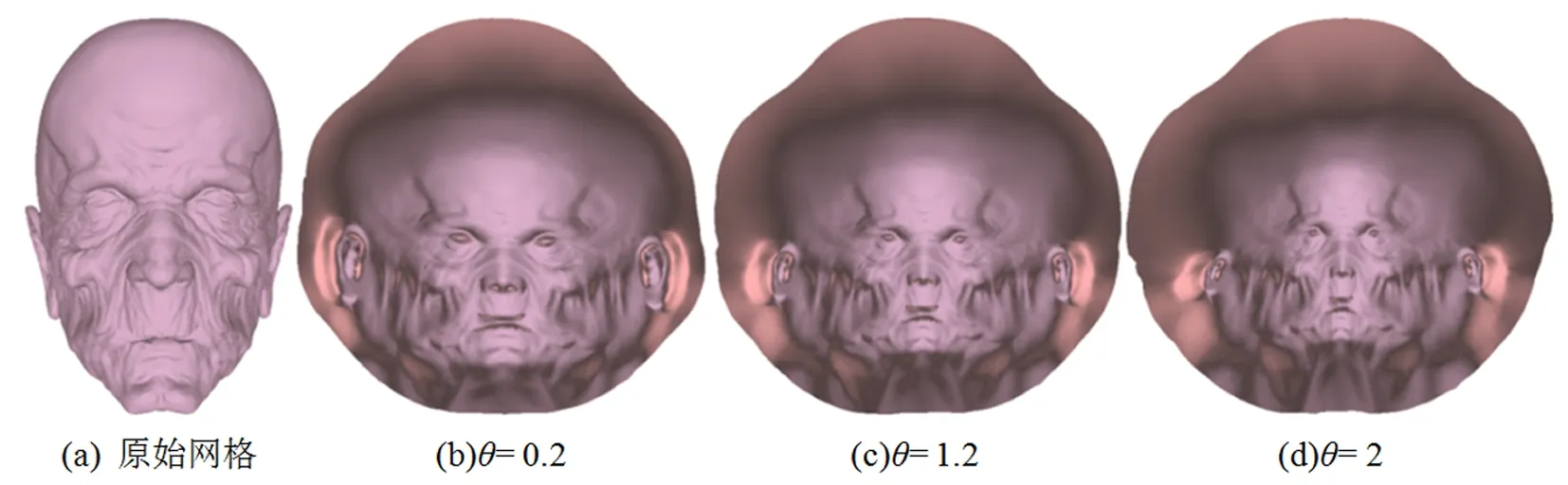
图3 Head模型: 不同拉伸指数对应的自由边界的平面参数化

在球面参数化中,展示不同的拉伸因子所对应的球面参数化结果,如图4所示。 由于球面结构与平面结构是不同的, 球面参数化结果应为拉伸区域和收缩区域相结合, 才能构成一个零亏格的球面, 而不能靠单纯的拉伸或者收缩而得到。为了更加清晰地显示每个拉伸因子所对应的球面参数化的整体细节, 首先将球面参数化结果投影到正方体上, 然后将正方体沿棱上的顶点路径进行切割, 形成单边界的网格模型, 最后将单边界的正方体网格等距的展平到平面上。

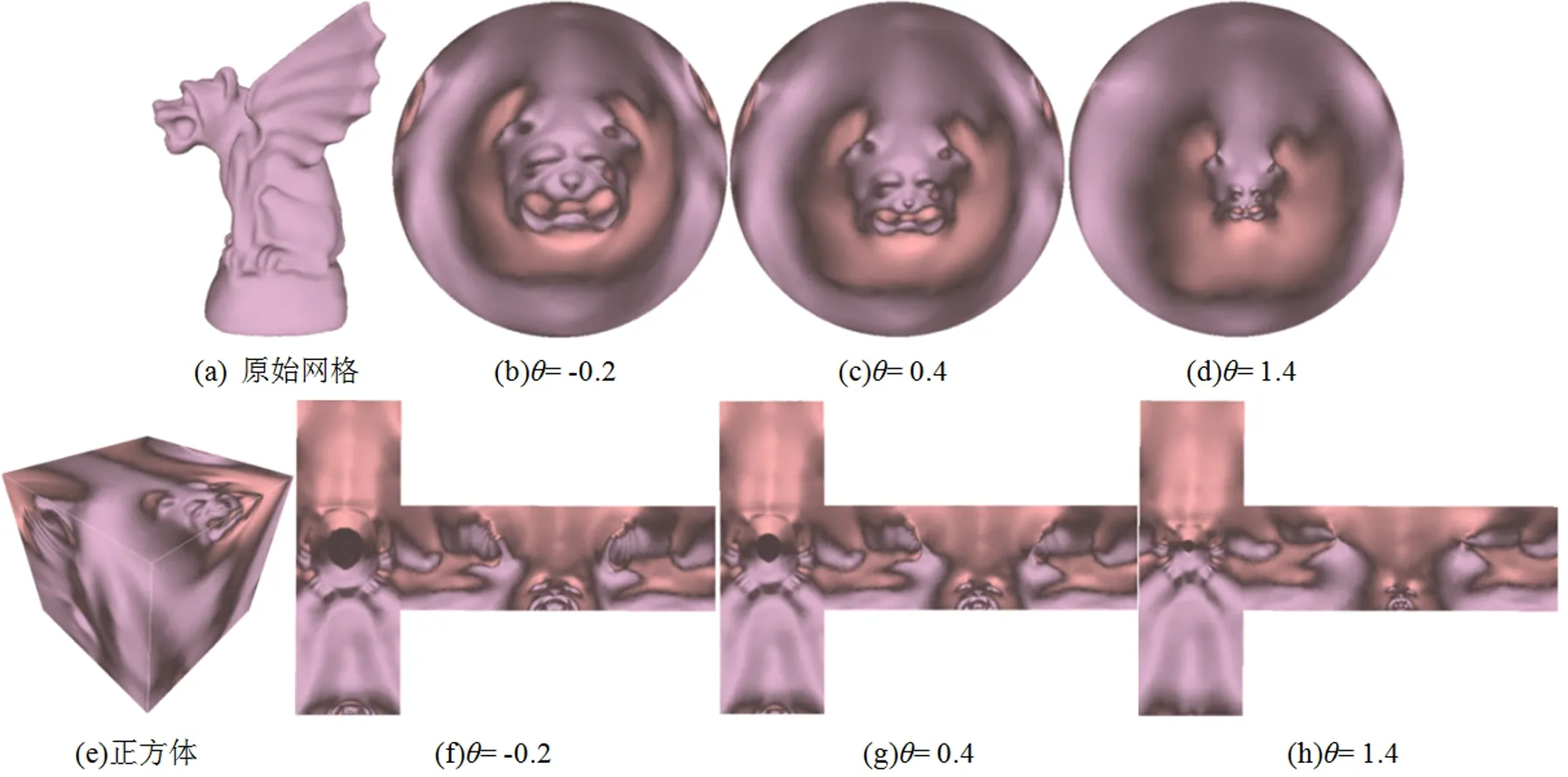
图4 Gargoyle模型: 不同拉伸指数对应的球面参数化

3数值实验

该实验均在i7 3.8GHz CPU, 32GB内存的PC机上运行, 采用MATLAB编程实现。比较了各种参数化算法的扭曲度量和运行时间, 然后将参数化所对应的纹理映射加以比较。

3.1 固定边界的平面参数化和纹理映射的比较

在实验1中, 将可拉伸的ARAP++曲面参数化算法与其它经典平面参数化方法进行比较, 这些方法包括Intrinsic[10], Stretch[15]和Progressive方法[3]。选择这3种经典方法作为比较对象主要是因为Intrinsic方法是凸组合方法，它是许多参数化方法改进的基础。Stretch方法是可拉伸的参数化方法，用来验证该项研究的拉伸度量。Progressive方法是近3年提出的新方法，一种渐进的参数化方法。该研究方法中的拉伸因子分别为θ=-0.2和θ=1。图5为固定边界的平面参数化和纹理映射的比较。

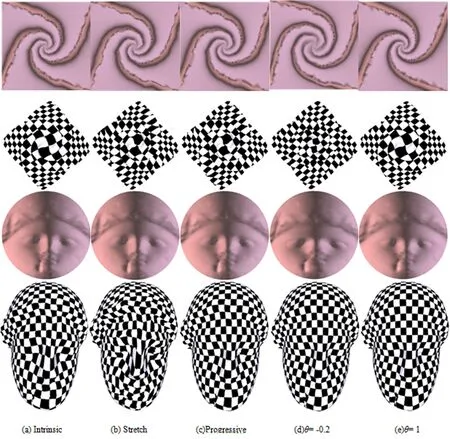
图5 固定边界的平面参数化和纹理映射的比较

如图5所示,主要比较了固定边界的参数化结果和其对应的纹理映射。 实验中使用了2个模型 Flower和Egea, 在表1中, 比较了各种固定边界参数化方法的扭曲度量(角度、面积、拉伸)以及运行时间。通过分析试验数据可以发现, 该方法θ=1产生的角度扭曲为最小，该方法θ=-0.2产生的面积扭曲为最小，该方法θ=-0.2产生的拉伸扭曲为最小。在运行时间的比较中, 该方法略慢于Intrinsic和Stretch等2种方法, 但是好于Progressive方法。在纹理映射的比较中, 该方法θ=1由于产生的角度扭曲为最小, 所以得到的纹理映射保角效果为最好。该方法θ=-0.2较好地平衡了角度扭曲,面积扭曲和拉伸扭曲, 所以得到的纹理映射非常均匀美观。综上所述, 该方法与其它固定边界参数化方法相比较, 在扭曲度量和纹理映射等方面均有一定的优势。

表1 固定边界的平面参数化的扭曲度量和运行时间的比较

3.2 自由边界的平面参数化和纹理映射的比较

在实验2中, 将提出的可拉伸的ARAP++曲面参数化算法与其它经典平面参数化方法进行比较, 包括ARAP[1], BD-ARAP[12]和Progressive方法[3]。选择这3种经典方法作为比较对象主要是因为ARAP方法是原创方法，它是该参数化方法改进的基础。BD-ARAP方法是可调整参数的方法，从而达到保角和保面积的目的。Progressive方法与该研究方法类似，而且是近3年提出的新方法。该方法中的拉伸因子分别为θ=-0.2和θ=1。

如图6所示,主要比较了自由边界的参数化结果和其对应的纹理映射。实验中使用了2个模型 Julius和Nose, 在表2中, 比较了各种自由边界参数化方法的扭曲度量(角度、面积、拉伸)以及运行时间。通过分析试验数据可发现, 所得到的数据与固定边界的比较中保持一致。该方法θ=1产生的角度扭曲是最小的，θ=-0.2产生的面积扭曲和拉伸扭曲为最小。在运行时间的比较中, 该方法略慢于ARAP方法, 但是好于BD-ARAP和Progressive2种方法。在纹理映射的比较中, 该方法θ=1由于产生的角度扭曲为最小, 所以得到的纹理映射保角效果为最佳。该方法θ=-0.2较好地平衡了角度扭曲、面积扭曲和拉伸扭曲, 所以得到的纹理映射非常均匀美观。综上所述, 该方法与其它自由边界参数化方法比较, 在扭曲度量和纹理映射等方面均有一定优势。

图6 自由边界的平面参数化和纹理映射的比较

表2 自由边界的平面参数化的扭曲度量和运行时间的比较

3.3 球面面参数化和纹理映射的比较

在实验3中, 将可拉伸的ARAP++曲面参数化算法与其它经典球面参数化方法进行比较, 这些方法包括Convex[4], Hierarchical[13]和ARAP++方法[6]。选择这3种经典方法作为比较对象主要是因为Convex方法是球面凸组合方法，它是许多参数化方法改进的基础。Hierarchical方法是分层的参数化方法，可以保面积和拉伸。这种方法用来验证该研究的拉伸度量。ARAP++方法是该研究参数化方法改进的基础，用来验证该研究方法的改进效果。该方法中的θ=-0.2和θ=1。

如图7所示, 比较了球面参数化结果和其对应的纹理映射。实验中使用了2个模型 Bimba和Lion, 在表3中, 比较了各种球面参数化方法的扭曲度量(角度、面积、拉伸)以及运行时间。通过分析实验数据可发现, 该方法θ=1产生的角度扭曲是最小的。该方法θ=-0.2产生的面积扭曲要高于Hierarchical方法, 但是要好于其它2种球面参数化方法。在拉伸扭曲的比较中, 该方法θ=-0.2得到的结果是最好的。在运行时间的比较中, 该方法略慢于Convex方法, 但是好于Hierarchical和ARAP++2种方法。在纹理映射的比较中, 该方法θ=1由于产生的角度扭曲是最小的, 所以得到的纹理映射保角效果为最佳。该方法θ=-0.2较好地平衡了角度、面积和拉伸扭曲, 所以得到的纹理映射非常均匀美观。综上所述, 该方法在各种扭曲度量和纹理映射等方面均有一定的优势。

图7 球面参数化和纹理映射的比较

表3 球面参数化的扭曲度量和运行时间的比较

4结论

(1)该项研究提出了可拉伸的ARAP++曲面参数化算法, 它建立了局部全局参数化算法的从平面区域到球面区域过渡的桥梁,实现了从共形参数化到等距参数化的渐变过渡, 与以往一些经典算法比较时具有一定的优势, 也得到了较好的纹理映射结果。

(2)在理论上，拉伸因子θ与三维模型本身、参数化初值以及期望获得的参数化结果相关，通过分析θ与参数化质量之间的关系，可以总结出如下变化规律,θ的有效取值范围大致为[-2, 2], 当θ的取值小于零时，参数化结果的保角效果逐渐变差，而保面积和拉伸的效果会越来越好。

(3)该方法与一些经典参数化方法相比, 如凸组合方法、ARAP方法等，形式更加灵活，可以通过调整参数，来调整拉伸渐变，得到从保角度到保面积的一系列结果，另外，该种方法还可以从二维空间推广到三维空间，从而得到对应的球面参数化结果，因此本文方法在灵活性方面具有一定的优势。但是该方法也存在着局限性, 在选取计算拉伸因子θ的时候, 往往需要多次实验, 才能选取合适的阈值。