平面五杆机构的谐波-多目标遗传优化方法

王洪涛，李占贤

(1.华北理工大学 机械工程学院，河北 唐山 063210；2.河北省工业机器人产业研究院，河北 唐山 063010)

引言

平面并联五杆机构[1]是一种结构简单，并可适用于复杂恶劣应用环境的并联机构。它具有刚度大，可实现复杂运动轨迹、承载能力强等特点，在并联和混联机器人机构中得到广泛应用。

在平面并联机构设计中，尤其是平面五杆机构的设计，目前以基于工作空间的图解法为主,解析法的应用相对较少。在工程应用越来越多的高速运动环境中，对机构的动力响应特性及机构惯量等要求越来越高，使得图解法求解精度较低，不能同时满足多目标参数设计的缺点越发明显。解析法求解精度高，但需要大量的数学运算支持，这就使得可以快速得到机构设计参数的解析算法需求越发突出。

平面连杆机构的谐波特征参数方法是借助傅里叶级数理论，将连杆机构输出运动采用傅里叶级数方法进行描述[2]。在此基础上，借助快速傅里叶变换等数学工具，对连杆机构需要输出的谐波特征参数进行分析，找到机构谐波特征参数与平面机构尺寸之间的关系，从而得到基于连杆机构输出特征参数进行尺寸综合的一般方法。

遗传优化算法是一种基于生物自然选择与遗传机理的随机与优化方法，在1950年代被提出后，鉴于其在求解复杂优化问题中的良好适应性，在工业设计领域被广泛应用。 Deb等人提出NSGA-II(Non-dominated Sorting Genetic Algorithm 2)后，因其简单、高效、解集收敛性好等优点，在多目标优化领域被广泛应用。 孔民秀等[3]针对高速高加速度的平面并联机构，基于NSGA-II算法来求解多目标优化问题，进行尺度综合，提升了机构的动态性能。Baviskar等[4]提出了2种基于渐进式步长机制的算法，并与非支配排序遗传算法的搜索方式相结合，通过控制步长和分割数目等参数，在子代中生成更好的染色体，实现了快速收敛。李新超等[5]针对NSGA-II算法中非支配排序耗时多的问题，提出了偏好顺序淘汰的算法，减少了参与非支配排序解的数量,进而减少了求解时间，降低了偏好评价结果较差的个体解被选中后再进行交叉、变异的概率，提高了算法效率。

多目标遗传优化算法满足了多参数设计的要求，适用于求解较复杂的优化问题，但仍存在收敛速度慢、局部搜索能力不强、易陷入局部最优解等问题，不易得到稳定的全域最优解，且对算法初值敏感，对算法初值的依赖性较强。针对平面并联五杆机构的设计问题，采用多目标遗传算法计算最优解，算法初值问题是决定算法效率的重点。但在实际应用中，算法初值是不易确定的，造成了算法效率不高、收敛速度慢等问题。该项研究采用遗传优化算法与谐波特征参数法相结合的方法，主要解决遗传算法的初值问题、在初代搜索盲目、算法收敛速度慢的问题。

1平面五杆机构设计通用方程

平面五杆机构的谐波参数设计方法[6，7]，是在已知机构运动轨迹的情况下，无需建立特征库及其他参数，用解析的方法来计算出符合目标运动轨迹特征的机构设计参数。谐波参数法分析中，可将平面五杆机构分解为2个二自由度的开链机构，即CBA和CDE在铰点C处结合而成，可分解成2个铰链二杆组进行分析，如图1所示。

图1 平面五杆机构二杆组示意图

如机构在平面内向两侧方向运动轨迹对称，则两侧杆组参数一致，只需计算其中一侧杆组的参数即可。由谐波参数法的机构轨迹综合设计方程[2]有：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

式中，j=0，1，…，n，j≠k,m2=0，±1，…，±k, …，±(n-j)

2五杆机构参数计算

确定五杆机构中C点的目标轨迹，并将目标轨迹根据实际需要离散为若干个点，将C点位于坐标系中的位置采用傅里叶形式表示。然后利用谐波参数法将C点目标轨迹中离散后的点计算得到目标轨迹点的谐波参数。将计算所得到的设计参数带入平面五杆机构综合设计方程中，得到符合机构目标运动轨迹的杆组设计参数。

3 NSGA-II多目标遗传算法

NSGA-Ⅱ算法是在第一代非支配排序遗传算法(NSGA算法)的基础上改进而来，是在低维目标(2-，3-目标)优化问题中被应用最多的多目标遗传算法，它主要降低了非劣排序遗传算法的复杂性，相比NSGA算法具有运行速度快，解集收敛性好的特点。针对该项研究的三目标优化问题，NSGA-II算法相对适用。

NSGA-II算法中，初值的选择尤为关键，它决定了整个算法效率和计算成本。本研究根据平面五杆机构的设计特点和谐波参数法得到的设计初值，为达到提高优化算法效率的目的，对NSGA-II算法进行了针对性调整，具体算法过程如下：

(1)根据谐波参数法得到的平面五杆机构的设计参数分别生成初代个体，将初代种群扩充至指定种群数；

(2)将个体的3个目标参数分别计算出对应数值解。将得到的解进行可行性筛选，留下可行解；

(3)寻找非支配解，并进行分层操作，将解分成若干层，进行快速非支配排序；

(4)将父代种群和子代种群合并，生成新的父代种群；

(5)进行实数编码的二进制交叉操作；

(6)进行多项式变异，进行带有偏好性的二进制锦标赛选择；

(7)计算个体拥挤度；

(8)选择合适个体组成新的父代；

(9)循环5～8步骤，直到进化至最大代数。

4算例

综合平面五杆机构[7]，使平面五杆机构中C点在传动比为1的条件下，实现如图2所示目标运动轨迹。

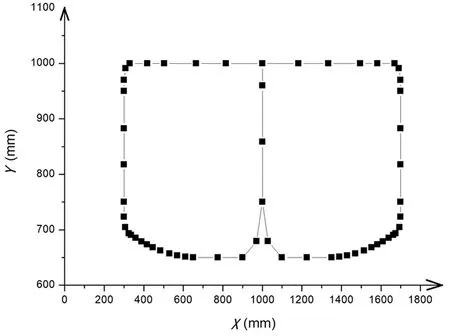
图2 平面五杆机构C点目标运动轨迹

将图2所示的点用谐波参数法进行表示，然后得到目标轨迹的谐波参数，因涉及的五杆机构的目标运动轨迹对称，故传动比为1，根据目标轨迹的特征，计算得到C点目标轨迹的-4到4次谐波参数，如表1所示。

表1 目标轨迹的谐波参数

将计算所得到的谐波参数带入平面五杆机构的综合设计方程，可以得到符合目标运动轨迹的机构杆组设计参数，如表2所示。

表2 计算所得二杆组设计参数

将上述计算所得到机构杆组设计参数应用于NSGA-II算法中，生成算法的初代个体，为达到提高优化算法效率的目的，对NSGA-II算法进行了针对性调整，具体算法过程如下：

(1)依据表2中计算所得的4组设计参数分别生成初代个体，并将初代种群扩充至指定种群数；

(2)将主动臂扭矩T、主动臂转角A、机构惯量IM，3个参数分别计算出对应数值解。将得到的解集进行可行性筛选，留下可行解；

(3)寻找非支配解，然后进行分层操作，将解分成若干层，进行快速非支配排序；

(4)将父代种群和子代种群合并，生成新的父代种群；

(5)进行实数编码的二进制交叉操作；

(6)进行多项式变异，然后进行带有偏好性的二进制锦标赛选择；

(7)计算个体拥挤度；

(8)选择合适的个体组成新的父代；

(9)循环5～8步骤，直到进化至最大代数。

其中，第(6)项中的偏好性选择，是根据计算所得的初值中主动臂与从动臂的长度，在主动臂及从动臂之和的总长度变化不超过5%的条件下，分别向增长与缩短2个方向变异，如主动臂长度增加，则从动臂长度减小。

4.1 平面五杆机构优化模型

设计变量：x、y、u、v、w，目标函数：

(10)

约束条件：

(11)

本算例的目标函数采用主动臂扭矩T、主动臂转角A、机构惯量IM，3个参数原因的如下：

(1) 主动臂扭矩T：在机构设计中，主动臂扭矩值关系到驱动电机的选取范围问题，电机扭矩范围又与电机的体积相关，电机体积又与两个主动臂间距相关，主动臂间距与机构的尺寸相关。所以，在五杆机构设计中，要尽可能的降低主动臂扭矩，以利于减小机构的体积，并降低电机选用要求；

(2) 主动臂转角A：在平面五杆机构设计重，尤其是有副杆的平面五杆机构设计中，需要避免机构杆组之间的干涉，这就使得主动臂转角范围相较理论值相应减小，所以在机构设计是需要尽量降低主动臂转角范围，在设计完成后进行仿真确认。同时，在高速机构设计中，降低了主动臂转角范围，会对机构的响应特性有正面影响；

(3) 机构惯量IM：在高速运动环境中，机构惯量需要满足一定设计要求，若机构的惯量过大，容易造成高速运动机构失效。机构惯量对机构的动态响应特性也有影响，在高速运动机构应用中要求机构惯量要尽量小，以提高机构的动态响应特性。

4.2 运行结果

由NSGA-II算法得到的Pareto最优解如图3所示。

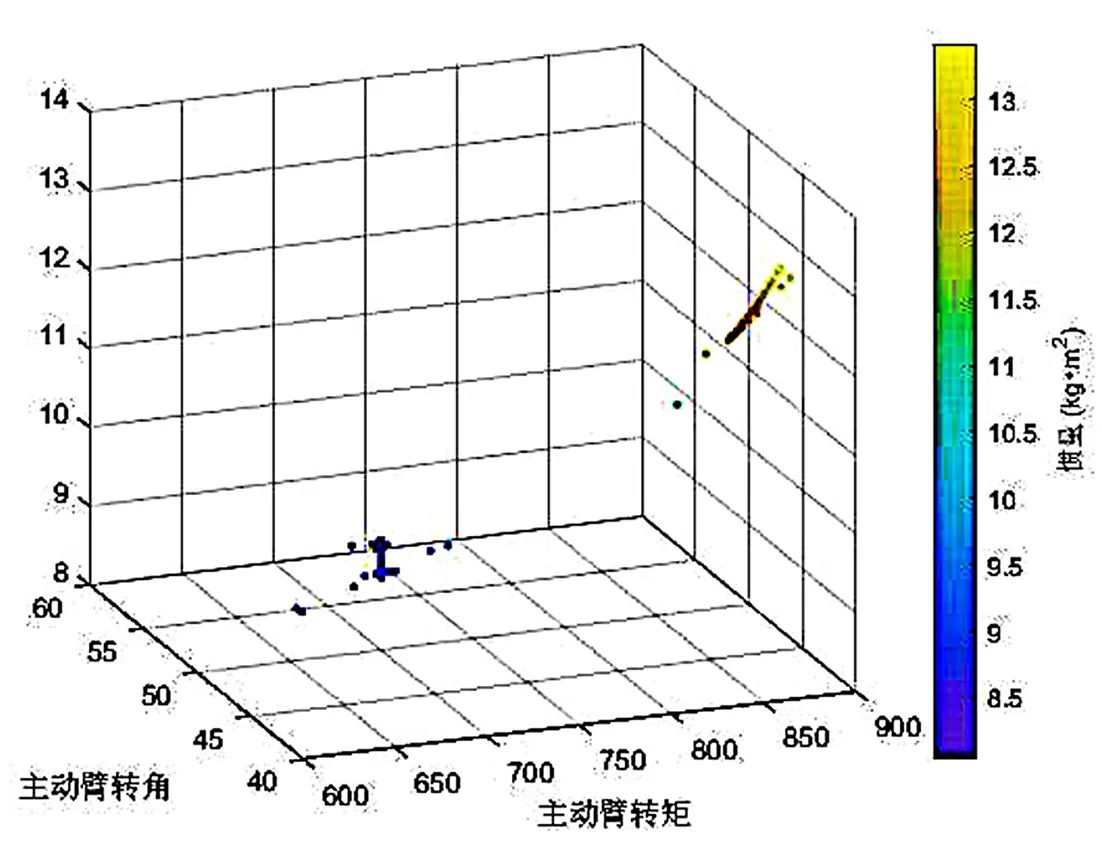
图3 Pareto最优解

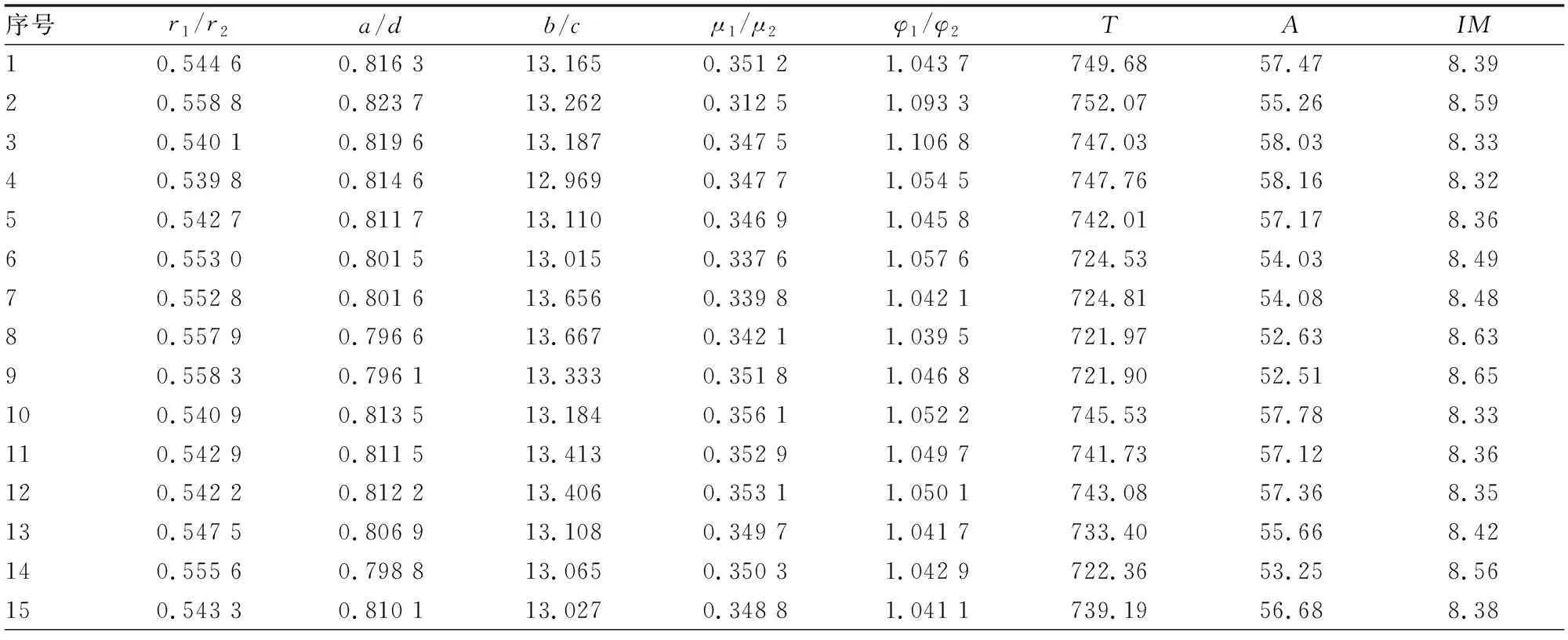
表3 多目标优化结果

5结论

(1)将平面五杆机构的谐波参数法与NSGA-II遗传优化算法相结合，对遗传算子加入偏好性选择，可以得到一个基于机构工作空间，不需要设计初值的多目标遗传优化设计方法，既满足了机构高速运动要求，同时又满足了机构驱动关节的低扭矩要求，且满足了平面机构的高响应特性要求。

(2)本设计方法所涉及的算法，根据机构的工作空间，可以单独计算出单个设计参数的范围，以供设计者参考。使设计者在选用驱动单元、确定机构运动节拍、设计机构强度等参数时提供可靠的取值范围，还可以根据具体设计要求，指定其中某个设计参数的优先级，使设计者在机构设计计算中，可以根据不同设计要求采用更加灵活实用的计算模型。

(3)应用谐波-多目标遗传优化算法后，程序的运算时间由无固定初值时，在300～400代左右收敛，运行时间为30～40 h，对比由谐波参数法计算遗传算法初值并生成初代个体值，对遗传算子进行偏好性改进后，算法在100～150代左右收敛，运行时间为12～18 h，算法效率可以提高50%以上。谐波-多目标遗传优化算法在解决了遗传算法的初值问题后，算法效率得到了大幅度提升，在平面五杆机构的设计中，提供了更为快速有效的解决方案。