基于改进PSO-BFO算法的WSN节点覆盖优化

龚瑞昆，邓朋浩

(华北理工大学 电气工程学院，河北 唐山 063210)

随着科技高速发展，无线传感器网络(WSN)凭借出色的性能优势，被广泛应用于众多领域，其中节点部署设计是WSN中的关键问题。在实际应用中，由于部署方式存在局限性，造成网络覆盖率低、资源浪费。设计合适的节点部署方式，能有效提高传感器的监测效率和网络中数据传输质量。

近年来，很多学者对WSN网络的覆盖优化方法进行了大量研究：文献[1-3]均提出改进的粒子群算法，对于惯性权重系数进行线性调整，收敛速度加快，但是由于粒子种群的种类比较单一，需要大量数目的粒子，容易造成覆盖区域重叠；文献[4]中宋婷婷，张达敏等人提出出改进的鲸鱼优化算法，在搜索阶段引入自适应步长，加快收敛速度和寻优效率，但是不能完全覆盖，留有覆盖空洞；文献[5]文森提出将粒子群算法和Voronoi图理论相结合，有效修补覆盖漏洞问题，但寻优效率并不十分高效；文献[6]梁樱馨提出基于PSO的改进细菌觅食算法，有效避免因"早熟"导致的局部最优现象，覆盖重叠区域以及盲区有所减少；文献[7,8]分别提出改进的果蝇优化算法和人工蜂群算法，缩短搜索时间，减少网络冗余度，但是随着传感器节点数目的增加,节点利用率逐渐减小；文献[9]中张雪，秦宇祺，张倩倩等人提出改进的自适应灰狼算法，引入非线性收敛因子和自适应调整策略，克服了容易陷入局部最优的缺点，但是在处理多模态测试函数时效果较差；文献[10]提出差分演化和粒子群优化算法，前期加强PSO的全局搜素能力，后期充分利用差分演化算法增强局部搜索能力，提高了寻优效率。

针对上述不足，该项研究提出一种基于改进PSO-BFO算法的WSN节点覆盖优化方法，该方法在解决WSN区域覆盖问题上，能够取得较好效果，与其他算法相比，其收敛速度更快，网络覆盖率更高，实验结果证明改进PSO-BFO算法更具优越性。

1 WSN节点覆优化模型

假设监测区域是一个二维平面,数字化为M×N个网格点，在区域内部署Z个传感器，所有传感器具有相同的感知半径R和通信半径Rs，且Rs≤2R。在仿真中使用0-1感知模型，把传感器感知区间抽象成为一个"圆盘"，假设传感器节点Ai的坐标为(xi，yi)，目标Bj的坐标为(xi，yi)，两点之间的距离为：

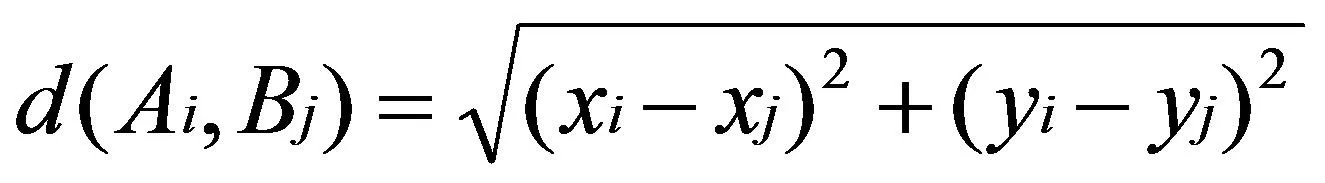
(1)

如果目标b在圆盘内，被传感器节点a感知到的概率为P(a,b)=1，否则 ，可用数学表达式(2)表示：

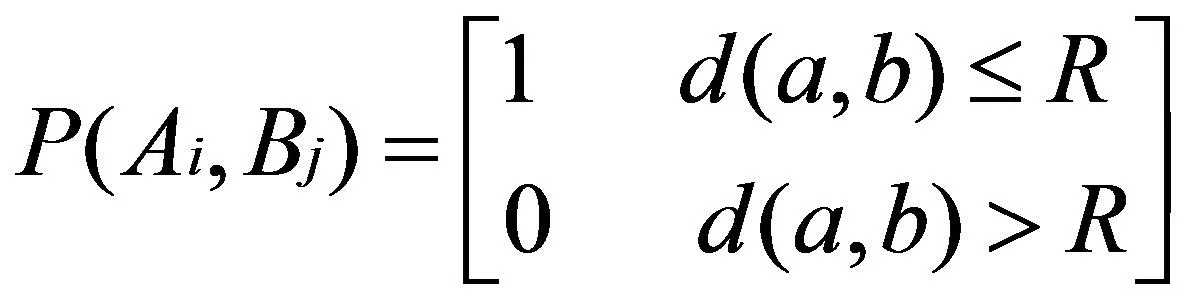
(2)

由于目标不容易被感知到，为了提高感知概率，需要多个传感器共同监测，则目标b被传感器节点集合G感知到的概率为：

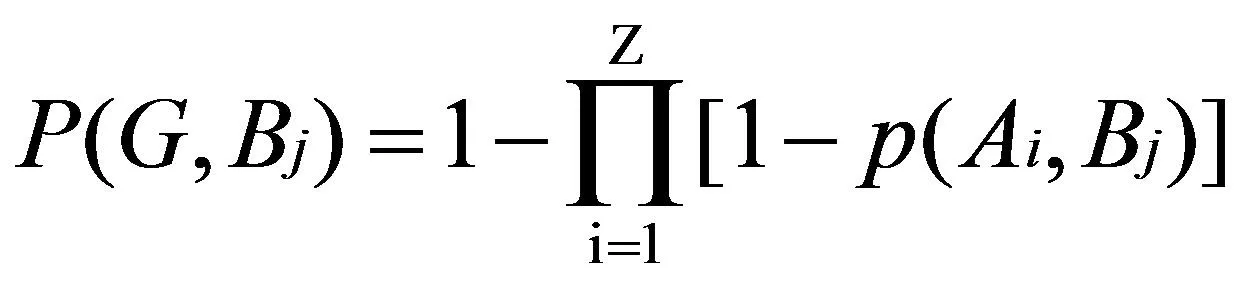
(3)

监测区域的覆盖率定义：

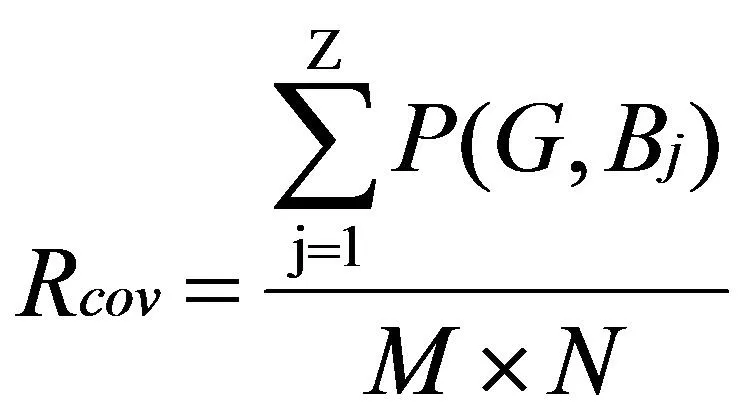
(4)

公式(4)是WSN节点覆盖优化模型目标函数，用改进的PSO-BFO算法求Rcov的最优值以提高覆盖质量。

2改进PSO-BFO优化算法

2.1 标准粒子群算法(PSO)

粒子群算法(PSO)是受集群动物启发而开发的一种智能算法，通过群体中的个体对信息的共享来使整个群体的运动实现对解空间的全局搜索。它最优越的地方是具有记忆能力，能记忆保留个体和群体的信息。

设粒子群空间有m个粒子，空间为D维，每个粒子都有一个初始位xi=(xi1,xi2,…,xid)T，都存在初速度向量Vi=(Vi1,Vi2,…,Vid)T，其中i={1，2，3…，m}。在算法优化过程中，会形成局部最优解pbesti和全局最优解gbest，粒子的飞行速度Vi根据2个最优解进行动态调整，直到粒子围绕一个最优点聚集。其中粒子速度和位置更新公式为；

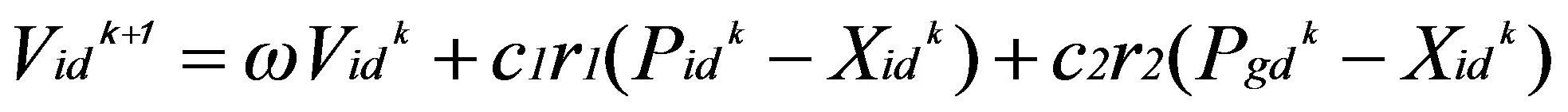
(5)

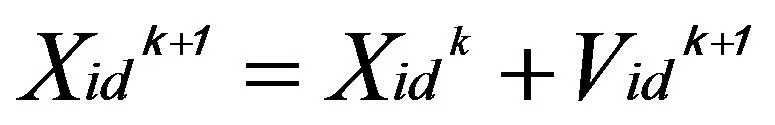
(6)

其中，ω是惯性权重系数，C1、C2是学习因子，r1、r2是[0,1]的随机数，k为迭代次数。XidK和Vidk分别为粒子位置和速度。

2.2 改进粒子群算法

通过观察粒子运动速度公式可知，ω能调节PSO的搜索能力，但是只是随着迭代次数线性减小，实时性较差。所以在PSO算法的惯性权重系数中引入进化因子和聚合因子，增强粒子的自适应能力。

2.2.1 进化因子和聚合因子

设粒子第k次迭代后的函数值为f(xik)，局部最优函数值为f(Pidk),全局最优函数值为f(Pgdk)。

对进化因子的定义如下所示。粒子i的进化程度定义为：

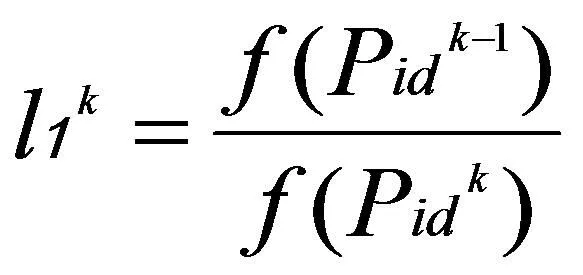
(7)

粒子群局部最优平均函数值的进化程度定义为：

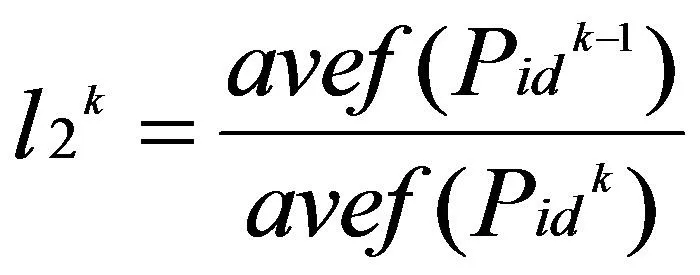
(8)

粒子群全局最优平均函数值的进化程度定义为：

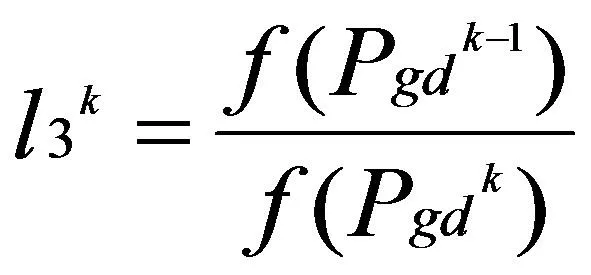
(9)

所以第k次迭代的进化因子可以表示为：

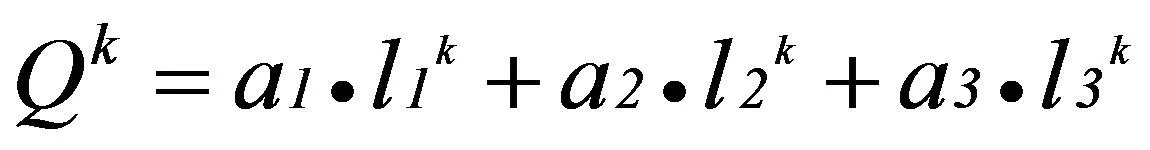
(10)

其中a1，a2，a3是[0,1]的系数且a1+a2+a3=1。

对聚合因子的定义如下所示,粒子的局部最优平均函数值定义为：

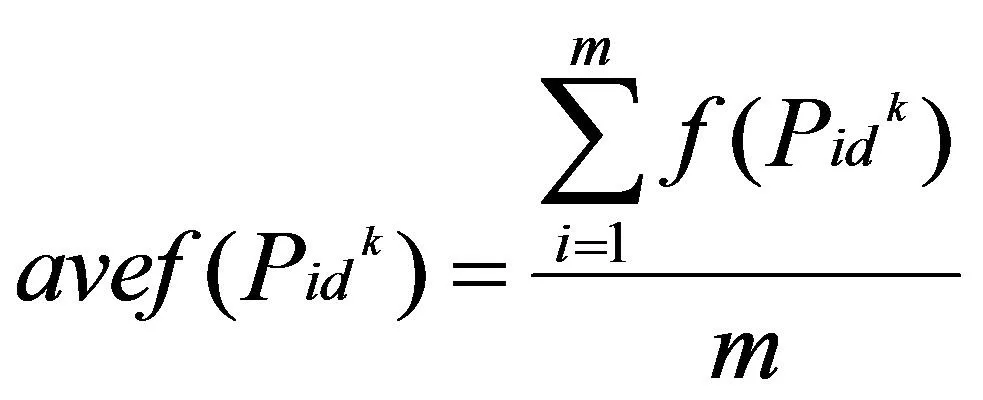
(11)

定义第k次迭代后，粒子平均函数值为：

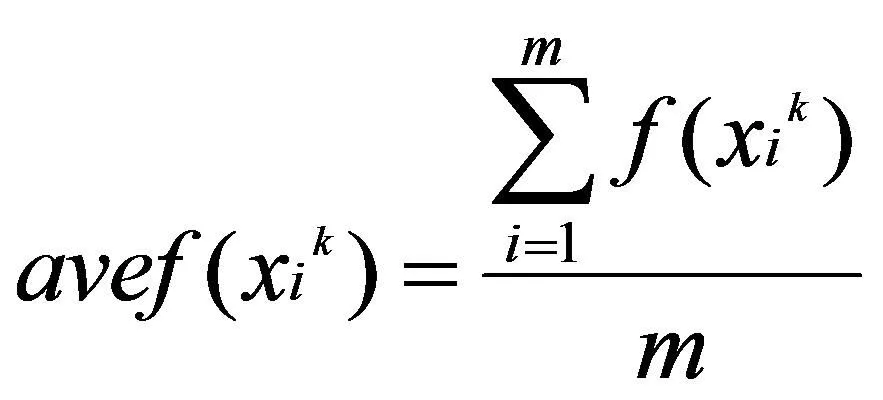
(12)

聚合程度其实就是当前粒子的平均函数值与局部最优平均函数值的接近程度，如公式(13)所示：

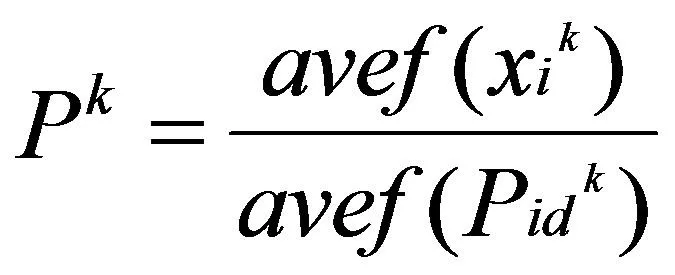
(13)

2.2.2 自适应惯性权重系数

根据引入的进化因子和聚合因子，自适应惯性权重系数公式可以定义为下式：

(14)

其中ω为初始惯性权重系数b1，b2，b3为调节系数，且b1+b2=1。Qk较大时，表示粒子进化速度缓慢，Pk较大时，表示粒子群的聚合程度较高。将自适应惯性权重系数代入公式(5)可得更新公式为：

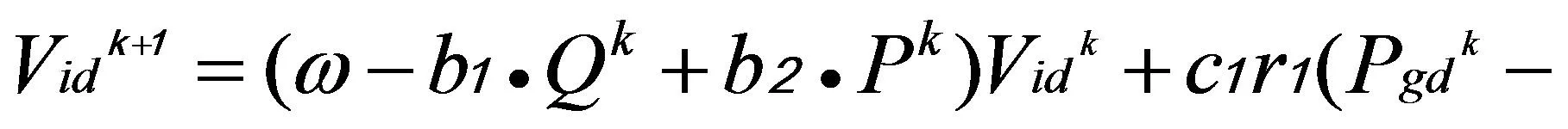
(15)

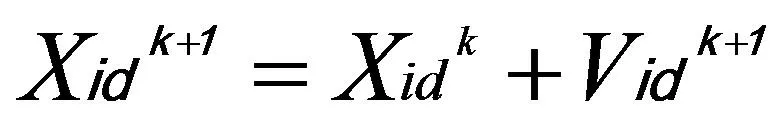
(16)

2.3 细菌觅食算法(BFO)

细菌觅食算法(BFO)是受细菌生长繁殖规律启发提出的一种新型仿生算法，算法简单、灵活，具有很强的鲁棒性和适应性，而且可以与其它各种算法结合生成新的算法，应用于不同的领域。BFO算法主要是通过趋化、聚集、复制和迁移4个操作来进行搜索寻优。操作如下：

趋化操作：细菌通过翻转和前进向富养区域聚集，位置更新公式如下所示：

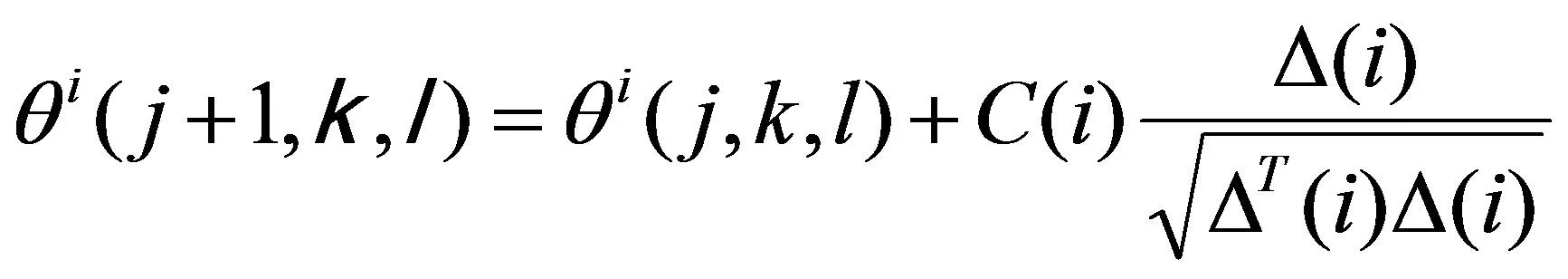
(17)

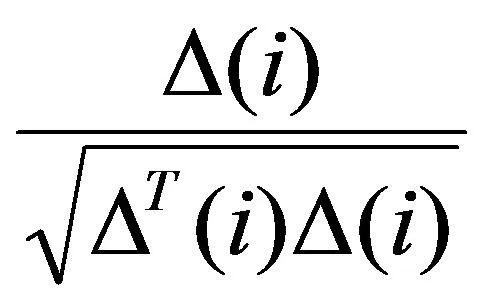
聚集操作：细菌之间会有信息交流，会通过释放引力和斥力信号来促使细菌聚集在一起，可通过修正细菌适应度函数来达到目的。细菌的适应度函数如下所示：

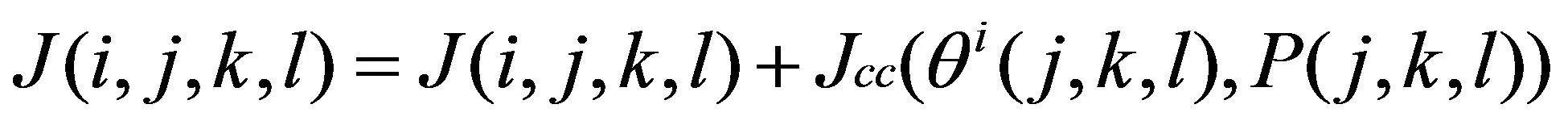
(18)

复制操作：对细菌的适应度函数值进行排序，活性好的细菌进行分裂复制，分裂所得细菌具有与母菌相同特性。

迁移操作：当环境发生改变或者其他突变情况，区域内的细菌会发生死亡或者迁移到其他地方。

2.4 改进细菌觅食算法

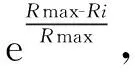
《兰纳克》是一次寻根之旅，是一个民族主义者和小说家表达对本民族命运关切的特有方式，同时它也是一个政治讽喻，以魔幻现实主义的方式呈现了内受经济衰退困扰、外逢强权政府压制的苏格兰社会状况，它更是整个西方工业社会的写照，揭示了现代城市生活各种状况的根源。在这部具有强烈“反乌托邦”色彩的小说中，格雷以讽刺的手法表达了对个人命运的关切和对社会政治经济的不满，批判了整个西方的政治意识形态。

(19)

其中，Rmax表示算法最大迭代次数，Ri表示细菌i当前迭代次数。自适应调节游动步长，改进后的细菌位置更新公式为：

(20)

2.5 改进PSO-BFO算法

PSO算法全局搜索能力强，但在搜索过程中容易陷入局部最优，BFO算法拥有较强的局部搜索能力，改进趋化操作中的搜索步长又极大提高了搜索过程中最优解的准确性。将BFO算法引入PSO算法中，用BFO中θi′(j+1,k,l)替代PSO中粒子所在位置Xidk，改进后的公式为：

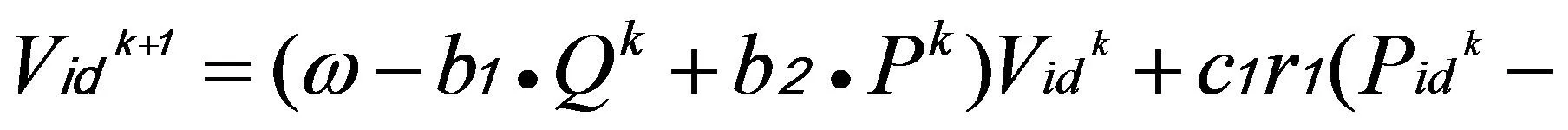
(21)

(22)

综上所述，改进PSO-BFO算法的基本思想是：前期采用PSO算法对监测区域进行全局搜索，通过PSO算法中的式(15)、式(16)跟踪粒子群的速度和位置，寻找全局最优解，寻找到当前pbest和gbest；后期的局部搜索则由BFO算法进行，通过式(21)、式(22)对区域进行局部搜索，提高PSO的局部搜索能力。2种算法优势结合，共同完成对监测区域的搜索。流程图如图1所示，算法主要步骤如下：

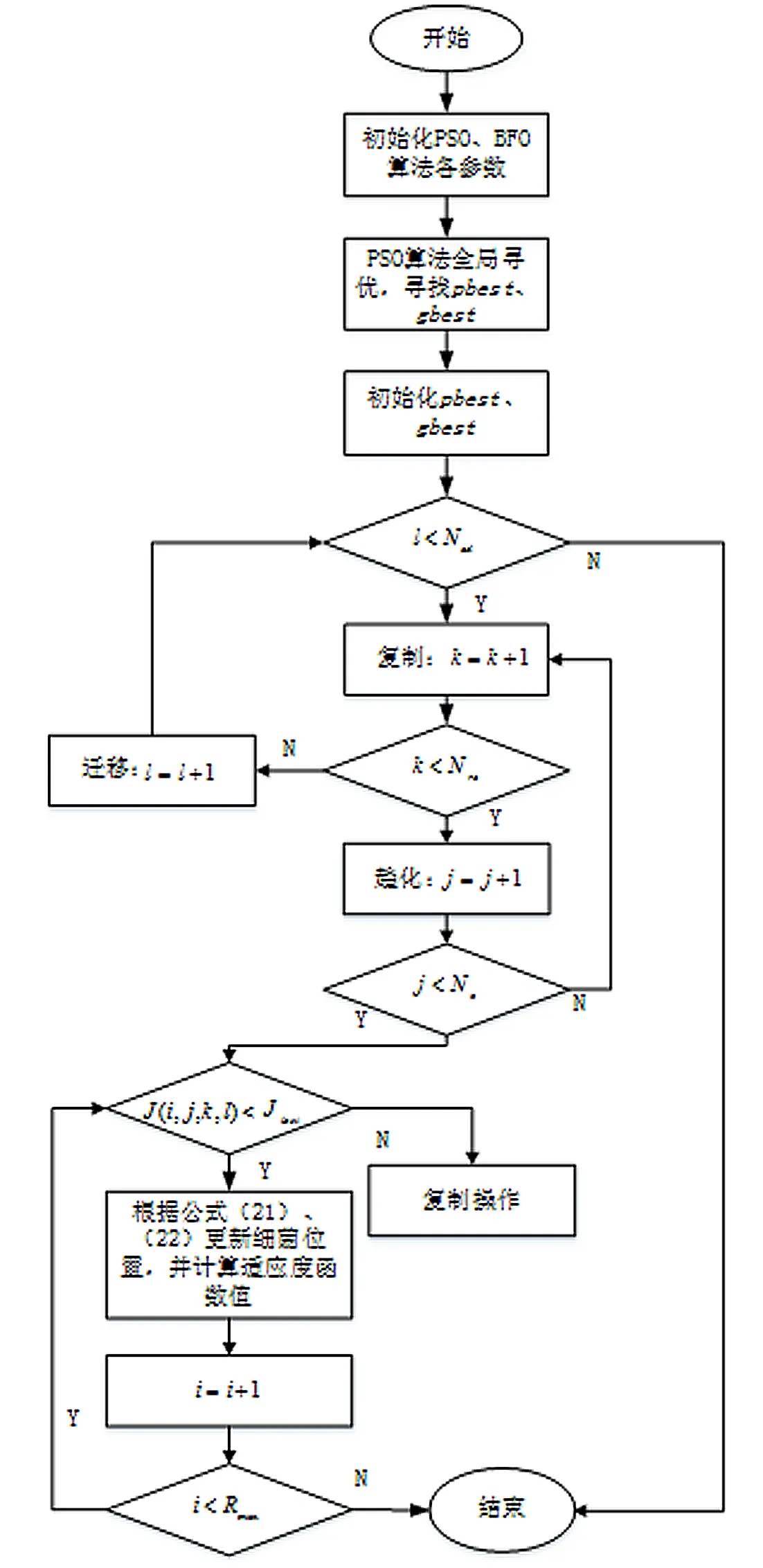
图1 算法流程框图

(1)初始化PSO、BFO算法中的各种参数；

(3)细菌翻转寻找局部最优，根据式(21)、式(22)更新细菌动态，并计算适应度函数；

(4)比较细菌的适应度函数值，当前值如果小于上一次的值，则返回步骤(3)，如果大于则进行下一步；

(5)趋化操作循环；

(6)聚集操作循环；

(7)复制操作循环；

(8)迁移操作循环；

(9)判断是否达到最大迭代次数，如果达到，结束算法；否则返回步骤4。

3仿真与性能测试

3.1 覆盖优化性能测试

通过在MATLAB中实验仿真，比较BFO算法、WOA算法和改进的PSO-BFO算法的节点覆盖效果。设置监测区域为20 m×20 m的二维平面，传感器节点设置为24个，感知半径为2.5 m，通信半径为5 m，迭代次数为100次。图2为3种算法的迭代曲线，图3为传感器节点随机分布图，图4为BFO算法单独使用时的节点优化分布图，图5为WOA算法优化的节点分布图,图6为改进PSO-BFO算法优化的节点分布图。

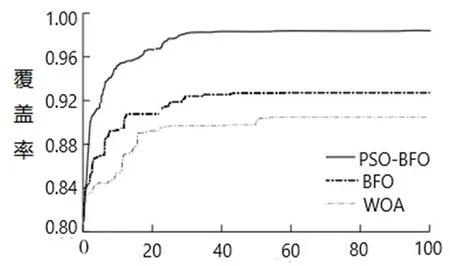
图2 3种算法的迭代曲线

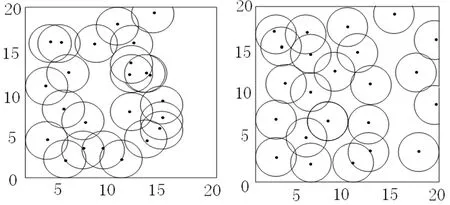
图3 传感器节点随机分布图 图4 BFO算法单独使用时的节点优化分布图

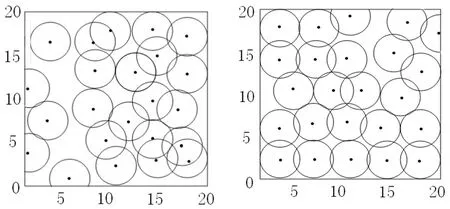
图5 WOA算法优化的节点分布图 图6 改进PSO-BFO算法优化图

通过图2可以比较出BFO算法、WOA算法和改进PSO-BFO优化算法对传感器节点部署的优化效果。该研究算法的覆盖率可达到97.5%，对比BFO算法的覆盖率92.7%，WOA算法覆盖率90.7%，覆盖率上升了4.8%和6.8%；观察传感器节点覆盖图可以发现，BFO和WOA优化算法虽然改善了一些传感器重叠问题，但还是存在覆盖不均匀，覆盖空洞的问题，而基于改进PSO-BFO优化算法的效果就比较理想，监测区域覆盖比较全，极大地改善了区域聚集重叠的现象，减少了资源浪费。

3.2 收敛性能测试

使用3种经典测试函数Griewank、Rosenbrock和Rastrigrin函数分别对BFO算法、WOA算法和改进PSO-BFO算法进行收敛性测试比较，其中以Griewank函数为例进行说明。Griewank函数为典型的多模态函数，二维图像如图7所示。Griewank函数数学表达公式如(23)所示：

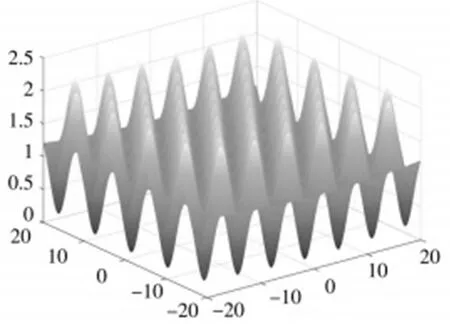
图7 Griewank函数图像

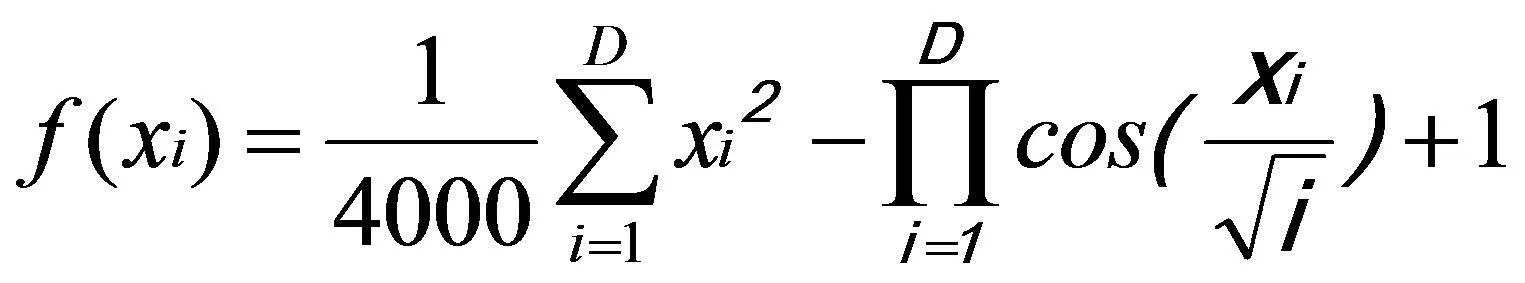
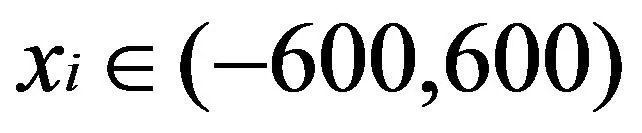
(23)

经过多次重复测试，改进混合算法PSO-BFO通过结合改进BFO算法和PSO算法的全局和局部搜索能力，有效避免陷入局部最优，极大加快粒子的收敛速度，其收敛效果优于BFO算法和WOA算法。收敛效果测试如图8所示。

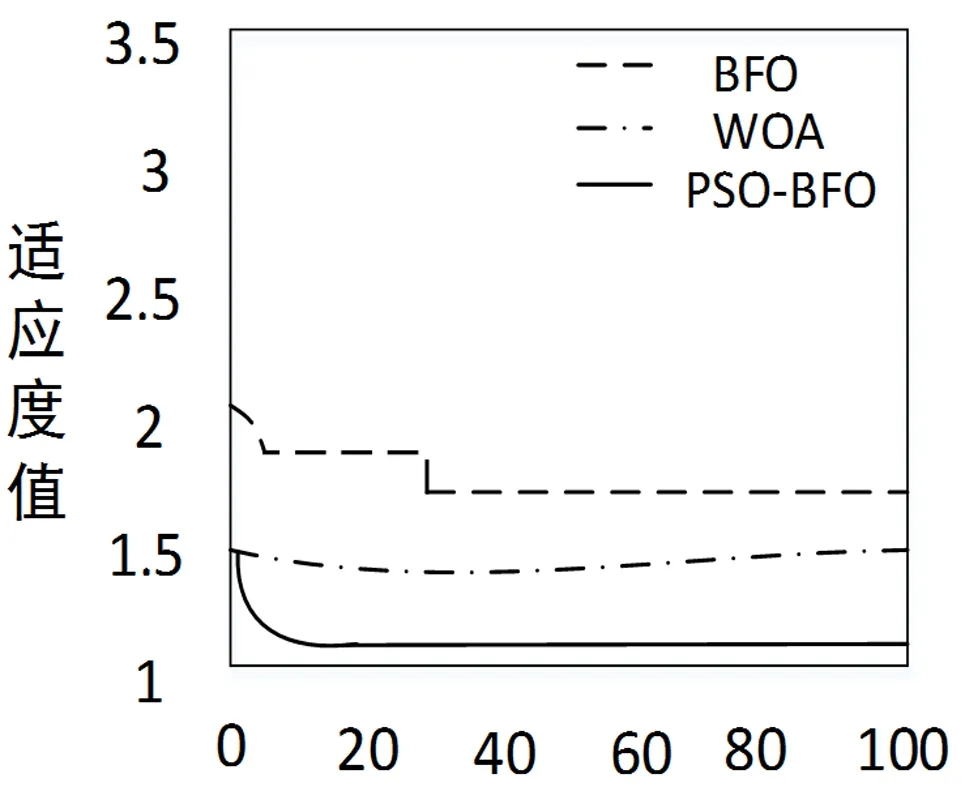
图8 迭代收敛效果测试

另外分别使用经典函数Rosenbrock和Rastrigrin函数对3种算法进行收敛性测试，3种函数测试结果如表1所示。

表1 3种算法的收敛效果

4结论

(1)该研究算法在解决传感器节点部署问题上更加高效，收敛速度更快，网络覆盖率更高，有效地减少了节点重叠聚集现象，减少了资源浪费。

(2)PSO-BFO算法也存在一些缺点，比如算法中参数较多，影响算法收敛速度，需要选择合适的参数才能最高发挥算法的性能。