铁尾矿砂钢筋混凝土梁抗弯性能研究

郭博宇，王兴国

(华北理工大学 建筑工程学院，河北 唐山 063210)

引言

随着经济建设的不断发展，工业与民用建筑越来越多，对混凝土的需求量越来越大。将铁尾矿砂替代普通河砂作为细骨料制成混凝土，既可解决天然河沙紧缺的问题，又可将铁尾矿砂回收再利用。近年来，国内外诸多学者在铁尾矿砂混凝土力学性能方面取得了很多研究成果[1-5]，为铁尾矿砂混凝土在工程中的应用提供了参考。在文献[1-5]中，对铁尾矿砂混凝土的抗压强度、弹性模量、应力-应变曲线进行了研究。研究结果表明，用铁尾矿砂代替河砂，会显著提高混凝土的抗压强度，其弹性模量略有提高，当铁尾矿砂混凝土的强度等级小于等于C40时，应力-应变曲线与普通混凝土的相近，当铁尾矿砂混凝土的强度等级大于C40时，下降段较普通混凝土的应力-应变曲线变陡。

在文献[6,7]中，通过对铁尾矿砂钢筋混凝土梁进行足尺抗弯试验，研究了铁尾矿砂钢筋混凝土梁在不同混凝土强度和配筋率下，对梁抗弯承载力、刚度、裂缝的影响。该项研究借鉴文献[6,7]中关于铁尾矿砂钢筋混凝土梁抗弯性能的试验结果，并建立数值模型对铁尾矿砂钢筋混凝土梁进行模拟，采用普通钢筋混凝土梁受弯公式计算抗弯承载力，三者对比分析铁尾矿砂钢筋混凝土梁抗弯性能。

1简支梁的受弯计算

1.1 试件设计

采用截面为200 mm ×400 mm，跨度为3 m的铁尾矿砂混凝土简支梁。箍筋采用直径为8 mm，加密区间距为100 mm，非加密区间距为200 mm的HPB300钢筋。架立筋采用 2 根直径为12 mm的HPB300钢筋。受拉纵筋采用HRB400钢筋。梁保护层厚度为20 mm，试验梁设计样图如图1所示。

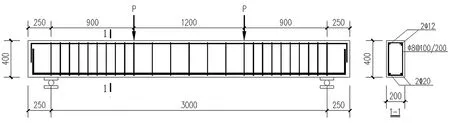
图1 试验梁设计样图

M=0.9P

(1)

式中：M为梁屈服弯矩，P为梁屈服荷载。

1.2 受弯构件正截面受弯承载力计算

1.2.1基本原理

单筋矩形截面受弯构件的正截面受弯承载力计算简图如图2所示，图中的x称为混凝土受压区高度，z称为内力臂。

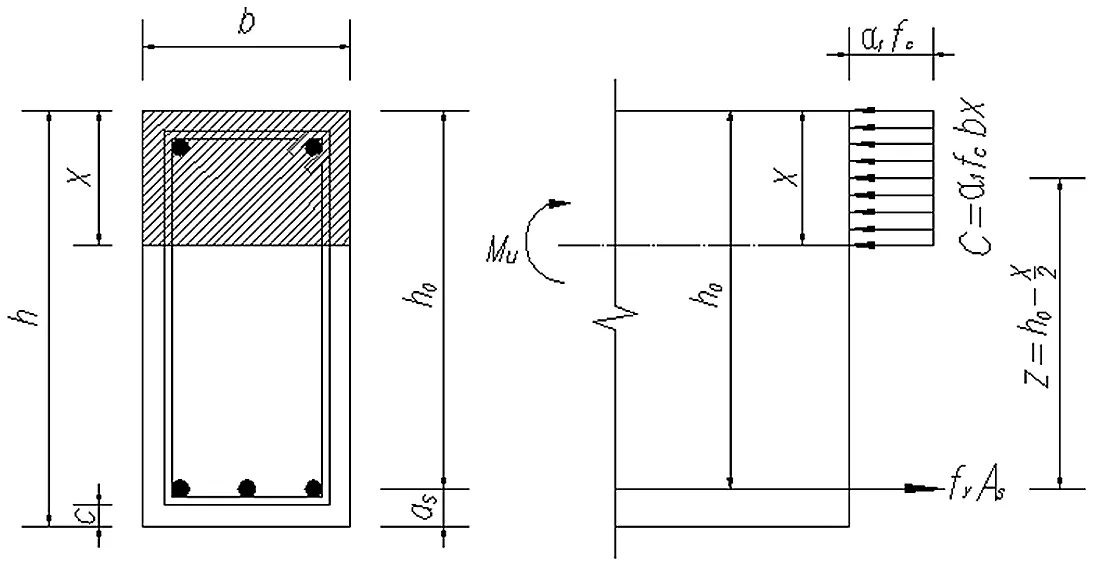
图2 受弯构件正截面受弯承载力计算简图

由力的平衡条件得：

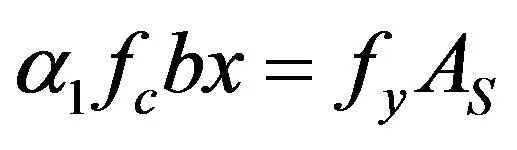
(2)

由力矩平衡条件得：

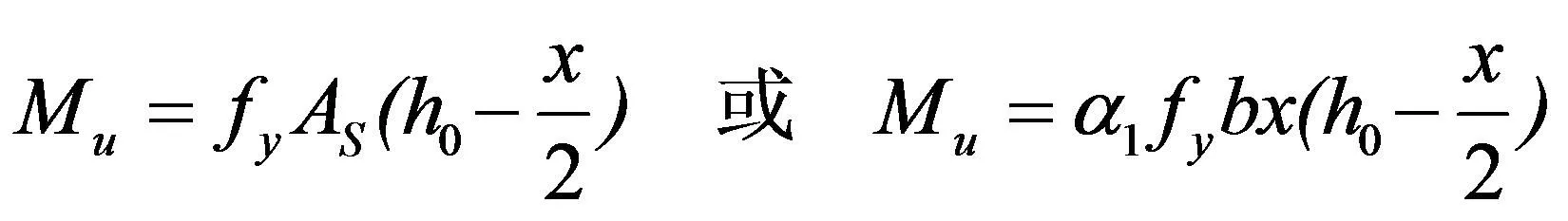
(3)

式中：Mu为正截面受弯承载力，单位为kN·m，a1为受压区混凝土矩形应力图的应力值与混凝土轴心抗压强度设计值的比值，fy为钢筋抗拉强度设计值，单位为MPa，fc为混凝土抗压强度设计值，单位为MPa，b为矩形截面梁宽度，单位为mm，x为混凝土受压区高度，单位为mm，As受拉区钢筋面积，单位为mm2，h0为截面有效高度，单位为mm，h为矩形截面梁高度，单位为mm。

1.2.2适用条件

为避免受弯构件发生少筋破坏，其一侧纵向受拉钢筋的配筋百分率应不小于0.2%和0.45ft/fy中的较大值，ft为混凝土抗拉强度设计值。为避免受弯构件发生超筋破坏，规定ξ≤ξb。ξ为相对受压区高度，ξb为界限相对受压区高度。

1.3 理论计算结果

在满足适用条件前提下，根据单筋矩形截面受弯构件的正截面受弯承载力计算原理计算梁的屈服荷载，计算结果如表1所示。

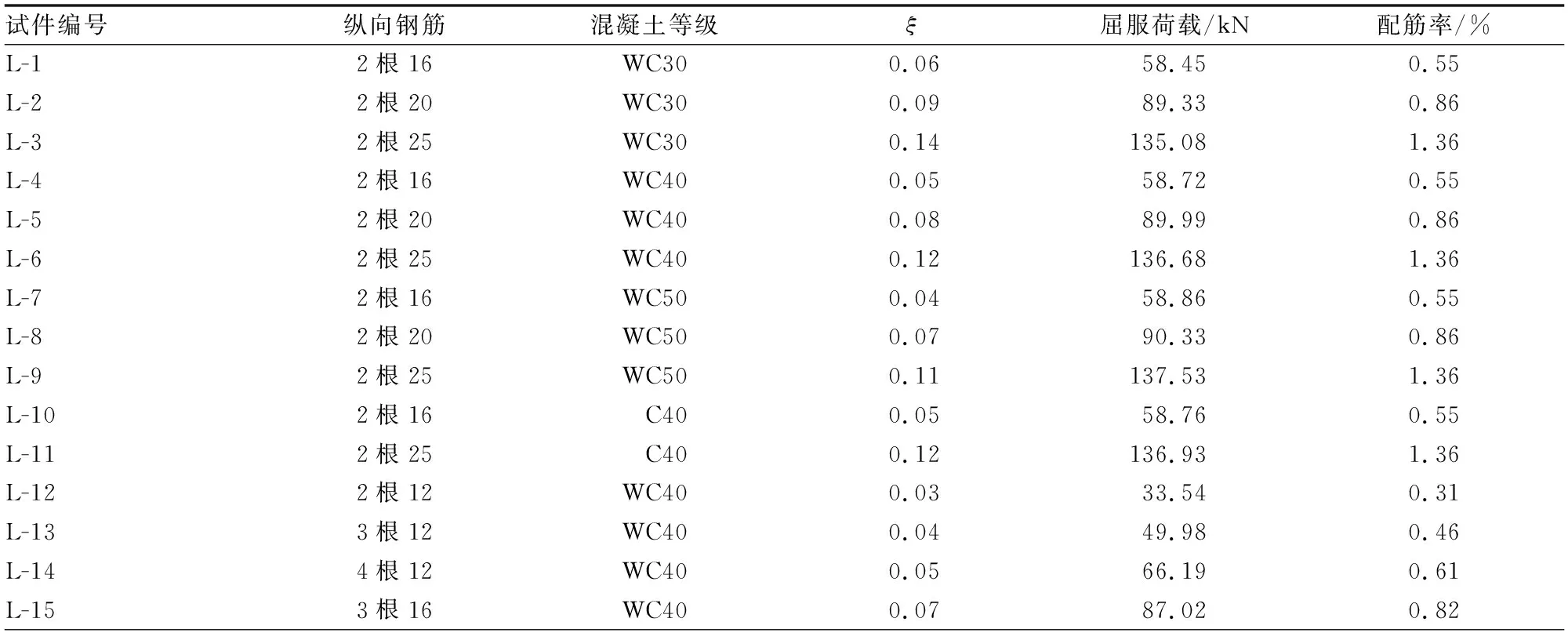
表1 铁尾矿砂梁的计算屈服荷载

2数值模拟

2.1 数值模拟参数

2.1.1弹性模量、抗拉强度、轴心抗压强度

用铁尾矿砂代替河砂，会显著提高混凝土的抗压强度[1,2],铁尾矿砂混凝土弹性模量略高于普通混凝土弹性模量[3]，根据《混凝土结构设计规范》(GB50010-2010)[8]提出的普通混凝土弹性模量、抗拉强度、轴心抗压强度简化计算方法，计算铁尾矿砂混凝土弹性模量、抗拉强度、轴心抗压强度。

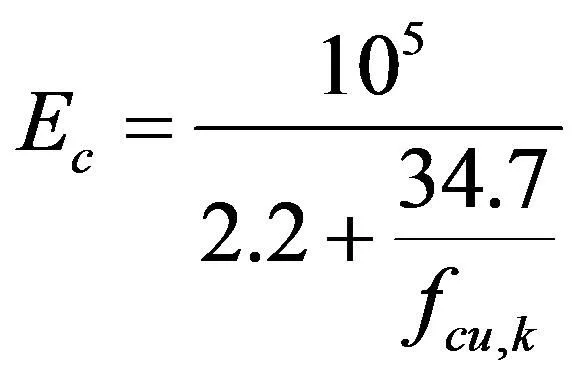
(4)

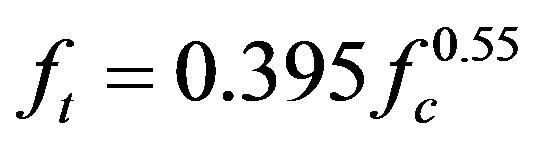
(5)

(6)

其中：强度等级C50及以下ac1混凝土轴心抗压强度与立方体抗压强度的比值取0.76，ac2为混凝土抗压强度脆性折减系数，强度等级C40的混凝土取1.0，强度等级C80的混凝土取0.87，中间线性插值。

2.1.2铁尾矿砂混凝土应力-应变关系

铁尾矿砂混凝土应力-应变关系采用由康洪震[5]提出的：

(7)

(8)

其中：x=ε/εp，y=σ/σp，fc混凝土轴心抗压强度，aa为上升段形状参数，ad为下降段形状参数。

根据文献[6]中不同强度铁尾矿砂混凝土立方块的抗压强度，用普通混凝土弹性模量、抗拉强度、轴心抗压强度简化计算方法和由康洪震[5]提出的铁尾矿砂混凝土应力-应变关系，画出不同强度铁尾矿砂混凝土应力-应变曲线，如图3所示。

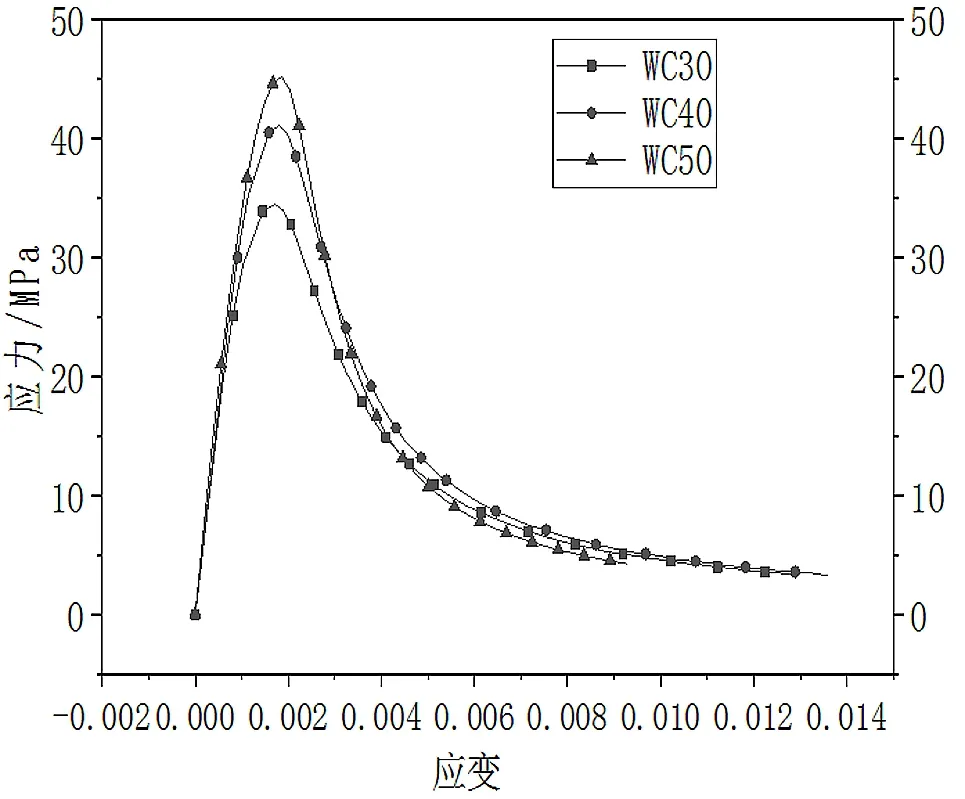
图3 不同强度铁尾矿砂混凝土应力-应变曲线

由图3可以看出，强度为WC50的混凝土其应力-应变曲线，较混凝土强度为WC40和WC30的应力-应变曲线的下降段陡。

2.2 数值模拟模型建立

钢筋骨架内置于混凝土梁内，混凝土采用八结点线性六面体单元C3D8R模拟，钢筋采用两结点线性三维桁架单元T3D2模拟，通过Abaqus建立数值模型，如图4所示。

图4 铁尾矿砂混凝土梁数值模拟模型

2.3 数值模拟结果

通过Abaqus建立数值模拟模型，得出模拟屈服强度，如表2所示。

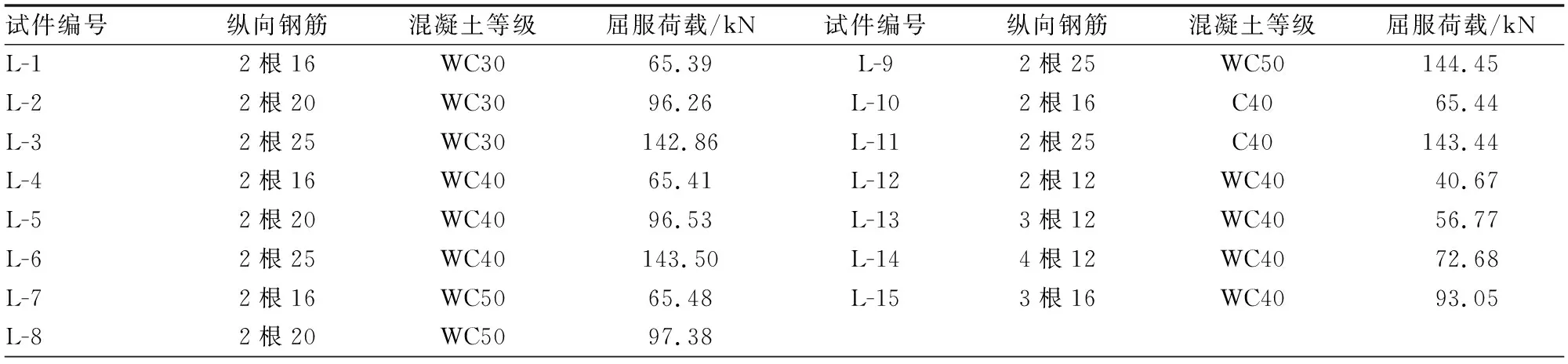
表2 铁尾矿砂梁的模拟屈服荷载

3梁抗弯承载力分析

3.1 结果对比

根据文献[6]中关于铁尾矿砂钢筋混凝土梁的抗弯性能试验结果，以及根据普通钢筋混凝土单筋矩形梁受弯公式计算的屈服荷载和数值模拟所得的屈服荷载进行对比，绘制对比图，如图5所示。

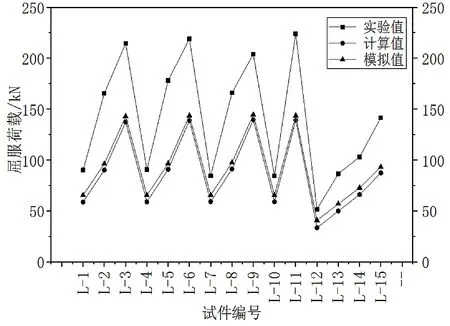
图5 梁屈服荷载实验值、计算值、模拟值对比图

由图5可以看出，由三者所得屈服荷载所绘曲线形状相似，模拟值略高于计算值，实验值大于模拟值和计算值。按照普通钢筋混凝土梁受弯公式计算的屈服荷载，架立筋未按照受压钢筋考虑，未考虑混凝土的抗拉强度，混凝土受压的应力-应变曲线采用的是抛物线上升段和水平段的应力-应变曲线，有限元模拟模型中的架立筋参与模型计算，考虑了混凝土的抗拉强度，应力-应变曲线有上升段和下降段，所以模拟值略高于计算值。有限元模拟时，铁尾矿砂混凝土的抗拉应力-应变曲线及拉伸损伤，采用的普通混凝土的，梁一般为带裂缝工作，受拉时刚度会退化，对模拟的屈服荷载影响较大；模拟时，铁尾矿砂混凝土弹性模量、抗拉强度、轴心抗压强度，根据普通混凝土弹性模量、抗拉强度、轴心抗压强度简化计算方法计算，钢筋的屈服应力为规范规定的360 MPa，导致采用参数均偏于保守，所以实验所得屈服荷载较大，通过公式与模拟所计算的梁抗弯承载力有可靠的储备。因此用有限元模拟铁尾矿砂混凝土梁抗弯承载力是有效的，用普通钢筋混凝土梁受弯公式计算梁抗弯承载力是合理的。

3.2 铁尾矿砂混凝土强度对梁抗弯承载力的影响

根据实验结果、计算结果、模拟结果，分别计算出WC30、WC40、WC50铁尾矿砂混凝土梁的抗弯承载力，图6为实验、计算、模拟结果下的铁尾矿砂混凝土梁的抗弯承载力。

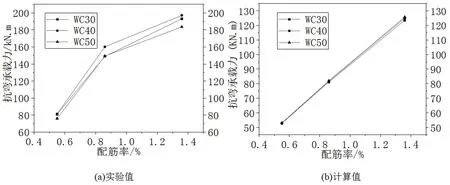
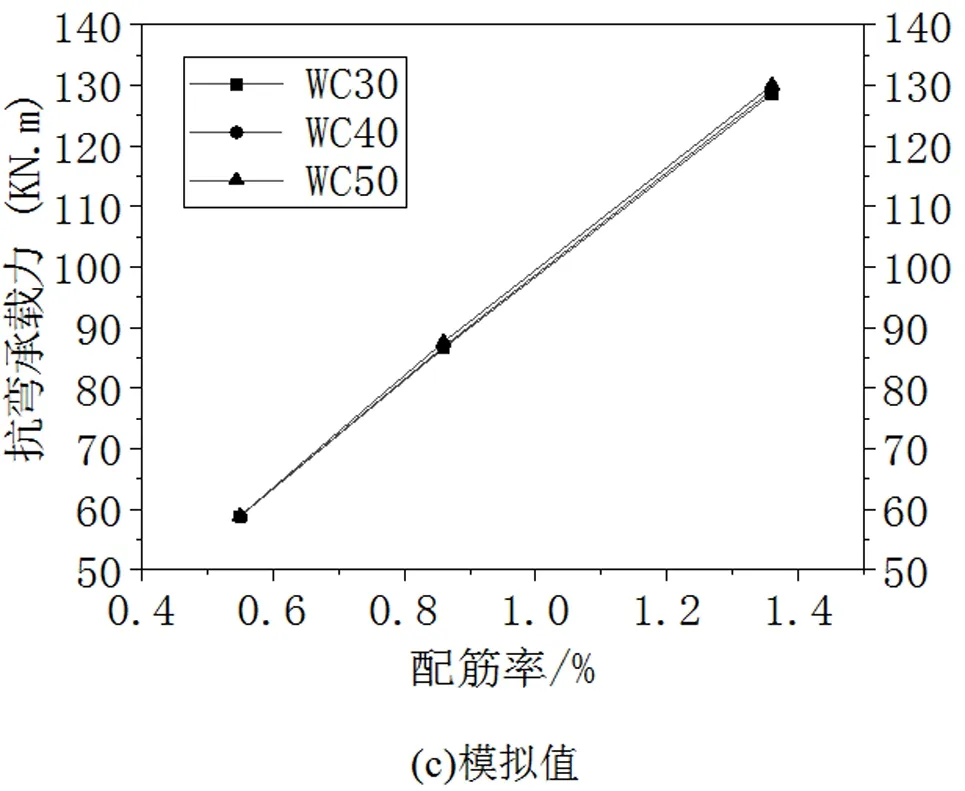
图6 铁尾矿砂混凝土梁的抗弯承载力

由图6(a)可以看出，不同强度下的铁尾矿砂混凝土梁抗弯承载力实验值变化不大。混凝土适筋梁破坏特点为：受拉区钢筋屈服，受压区混凝土压碎。强度小于C50的普通混凝土极限压应变为0.003 3，从图3可以看出，应变为0.003 3时，WC50的应力处于WC40和WC30之间，所以WC50的抗弯承载力略低于WC40的抗弯承载力。由图6(b)与图6(c)可以看出，不同强度下的铁尾矿砂混凝土梁抗弯承载力计算值、模拟值基本相同。所以，铁尾矿砂混凝土强度对梁抗弯承载力影响不大。

3.3 配筋率对铁尾矿砂混凝土梁抗弯承载力的影响

根据实验结果、计算结果、模拟结果，计算出如图7所示不同配筋率下WC40铁尾矿砂混凝土适筋梁的抗弯承载力。

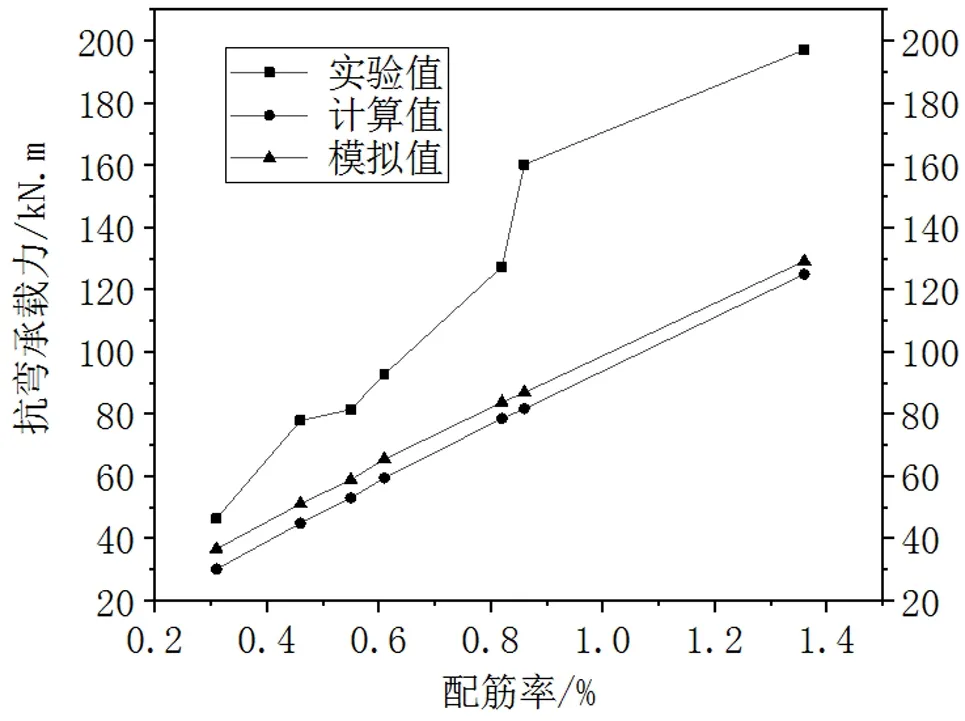
图7 不同配筋率下铁尾矿砂混凝土梁抗弯承载力

由图7可以看出，铁尾矿砂混凝土适筋梁抗弯承载力随梁配筋率的增大而增大。

3.4 铁尾矿砂混凝土梁与普通混凝土梁对比

根据实验结果、计算结果、模拟结果，计算出WC40和C40混凝土梁的抗弯承载力，如图10所示。

由图8可以看出，WC40和C40混凝土梁的计算值和模拟值基本相同，由于各构件材料性能不能保证完全一致，且加工构件存在安装误差等原因，实验值有所差距，但大致相同。铁尾矿砂混凝土梁与普通混凝土梁相比抵抗弯矩的能力大致相同。

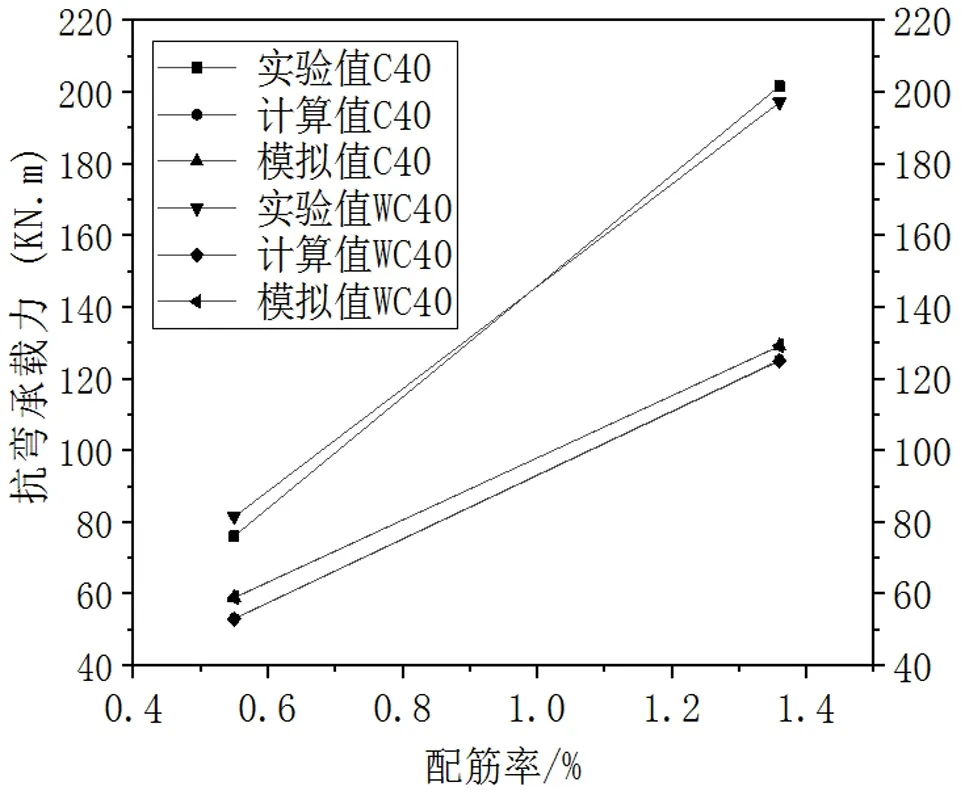
图8 WC40和C40混凝土梁的抗弯承载力

4结论

(1)用数值模拟的方法和普通钢筋混凝土梁受弯公式计算的方法，计算铁尾矿砂混凝土梁抗弯承载力是合理的。

(2)铁尾矿砂混凝土强度对梁抗弯承载力影响不大。

(3)铁尾矿砂混凝土适筋梁抗弯承载力随梁配筋率的增加而增大。

(4)铁尾矿砂混凝土梁与普通混凝土梁相比抵抗弯矩的能力大致相同。