一类Kirchhoff 型弱耦合系统的多重解的存在性

魏其萍 ,王跃 ,熊宗洪, ,王守财

(1.贵州民族大学 数据科学与信息工程学院,贵州 贵阳,550025;2.贵州大学 数学与统计学院,贵州 贵阳,550025)

Kirchhoff 在1876 年首版的文献[1]提出模型为不同的物理常量。由于该问题具有丰富的物理背景,因此与该模型相关的各种问题的理论研究在各个领域受到了广大关注。对于更一般的时定情形为

此时a和b都是常数,Ω是NR 中满足某些假设条件的子集。在无界域上,文献[2]考虑了方程(1)含有负模量的临界指数情形,利用山路引理和艾克兰变分原理获得解的存在性;文献[3]利用代数分析方式获得无穷多解;在第二边值的情形下,文献[4]利用喷泉定理得到了方程(1)无穷多径向解的存在性;文献[5]推广方程(1)到

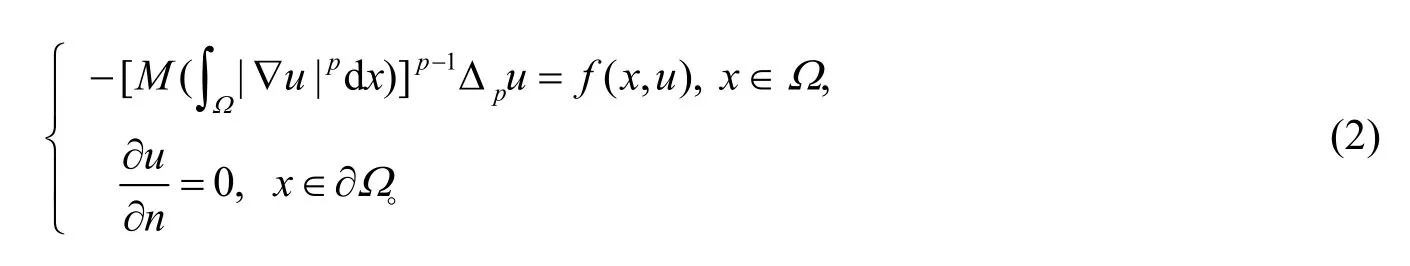
其中Δp表示p-Laplace 算子,作者通过变分方法和临界点理论获得了方程(2)非平凡解的存在性;文献[6]通过变分方法得到方程(2)在不同条件下分别存在1 个和3 个在W1,p(Ω)上的弱解;文献[7]通过代数分析方法给出无穷多解;当g(x,u)=f(x,u)-qu时,文献[8]通过G-环绕定理和变分方法以及集中紧性原理等方法和分析工具分别得到了方程(1)解的存在性和多重性;对于b为零的情形,文献[9]推广到分数阶问题解的对称性与单调性,文献[10]则利用半群理论得到退化抛物方程的全局吸引子。更多的研究,还包含了第一边值条件和不受边界约束等情形[11-13],而在文献[14]中叙述了大量关于基尔霍夫问题的理论和结果。由于在文献[15]中提到了如下p(x)-Kirchhoff 型的非局部椭圆系统

1 主要结果

假定Ω⊂RN(N≥ 1)是具有光滑边界∂Ω的区域,讨论耦合系统

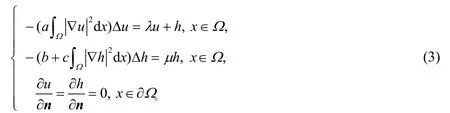
其中a,b,λ＞0,待求函数(h,u)∈C2(Ω)×C2(Ω)为系统(3)的解。本文创新点在于使用更为简单的代数分析方法解决耦合系统解的存在性以及多重性问题,主要结果如下。

注：容易得出,当h(x) ≡ 0时系统(3)存在无穷多解。

2 结果的证明

系统(3)中第2 个方程的解可以作为1 个扰动函数作用到第1 个方程中而形成弱耦合系统,为此须先解决系统(3)中第2 个方程解的存在性问题,即考虑以下方程

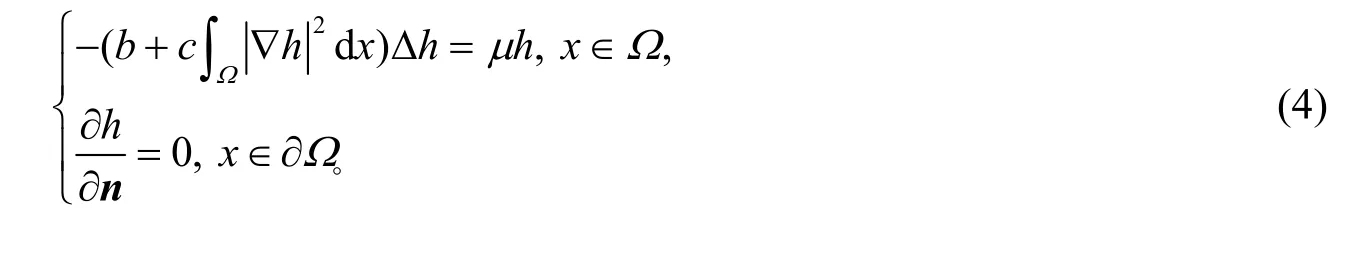
的解并将其代入

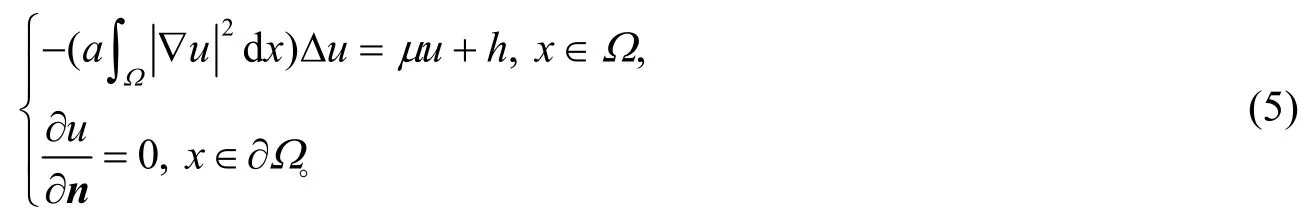
从而求取方程(5)的解,进而获得系统(3)解存在的情形。

在文献[16]中阐述了如下二阶椭圆特征值问题

3 结论

本文用本征值问题以及代数分析的方法获得耦合系统(3)的无穷多经典解,所得到的解主要用来描述系统振动在横向上形成的共振现象,它可以视为Kirchhoff 型问题的混合作用模型,两种流体弹性材料混合在一起时,如果一种弹性材料受力横向振动用u=u(x)表示,另一种弹性材料与之附着受力横向振动用h=h(x)表示,则解描述了具有相同振动频率时另一种振动对一种振动的促进或者牵制。