基于EM 算法的工业机器人抓取控制研究

卢晓玲,孙自昌

(安徽汽车职业技术学院 机电工程系,安徽 合肥,230601)

工作的稳定性使得工业机器人在汽车生产、机械产品自动化生产制造、高危设备安装等领域具有十分广泛的应用[1]。抓取是工业机器人的基本操作任务,在执行抓取任务的过程中工业机器人需要结合待抓取物体的位姿信息来调整机器人的关节,从而实现对各种位姿状态下物体的抓取[2]。具有视觉的机器人通过视觉获得待抓取物体的位姿信息,采用运动学逆解的方法获得机器人的关节坐标[3]。该方法能够使得工业机器人实现对物体的自适应抓取,但是对机器人的操作者具有相对比较高的要求,同时对具有冗余自由度的机器人来讲,获取稳定运动学逆解也比较困难[4]。机器学习的快速发展使得对机器人抓取的控制由模型驱动向数据驱动发展,通过相机获得待抓取物体位姿观测数据,由位姿观测数据通过机器学习理论获得工业机器人的关节变量数据,从而更好地对机器人抓住进行控制[5]。基于此,本文采用最大期望算法(EM)对工业机器人抓取控制进行研究,降低对机器人操作者的要求,确保机器人可以在较大范围内对物体的抓取。

1 工业机器人抓取控制

1.1 工业机器人抓取控制原理

工业机器人在执行抓取任务时要根据所抓取物体的位姿对自身进行调整。设oi为所抓取物体的观测变量,ri为与之对应的工业机器人关节变量,在oi和ri之间存在映射关系f,即[6]f:oi→ri。

设xi=[ri,oi]T为工业机器人关节变量和所抓取物体观测变量组成的样本,记

那么X为通过工业机器人示教得到的训练样本集。工业机器人在执行抓取动作时要先通过训练样本集进行学习,获得由所抓取物体的观测变量o到与之对应工业机器人关节变量r的映射关系f。对于所要抓取的观测变量为onew的新物体,通过映射关系f可以获得工业机器人的关节变量rnew。

对工业机器人抓取动作控制的关键是选择合适的模型去描述映射关系f,本文采用正态分布混合模型去描述映射关系f,通过EM 算法将训练样本集X划分为几类,每一类服从一个正态分布[7]。采用正态混合分布模型对工业机器人抓取进行控制的流程如图1 所示。

图1 工业机器人抓取控制流程图

通过对工业机器人示教来获得包含观测变量和机器人关节变量的训练样本集,采用基于EM 算法的正态混合分布模型对训练样本集进行训练,达到对样本分类的目的,其中每一类样本均对应不同的工作区域,同时构建物体观测变量和工业机器人关节变量之间的映射关系。工业机器人在执行抓取物体的动作时,借助相机获得待抓取物体的观测变量,计算观测变量来自于各个正态分布的后验概率,选择后验概率最大的正态分布获得工作机器人的关节坐标,从而驱动工业机器人实现对待抓取物体的抓取控制。

1.2 正态分布混合模型

EM 算法是基于极大似然估计的优化算法,采用EM 算法来训练正态混合分布模型,从而得到混合模型的参数[8]。对正态混合分布模型的参数初始化之后,通过E 步和M 步的交替迭代来不断地更新混合模型的参数。

E 步:计算样本xi来自于第k个正态分布的权重rik,那么

M 步:聚类参数更新,即

其中,

采用EM算法对训练样本集进行正态混合模型训练,最终训练样本集被划分为m类,每一类样本都服从一个正态分布,同时对应于工业机器人工作区间的一个区域[9]。

1.3 工业机器人关节变量预测

基于EM 算法的工业机器人完成物体抓取是通过物体观测变量获得机器人关节变量。假设待抓取物体通过相机获得的观测变量为newo,那么onew来自于第k个正态分布的后验概率为[10]

不妨假定第k个正态分布对应的后验概率最大,那么选择第k个正态分布来对工业机器人的关节变量进行预测。对第k个正态分布的均值向量μk和协方差矩阵∑k分块,即

其中,μr、μo分别为训练样本集中机器人关节坐标均值和物体位姿坐标均值;Krr、Koo分别为机器人关节变量协方差和物体位姿观测变量协方差;为观测变量和关节变量协方差。

待抓取物体的观测变量onew和与之对应的工业机器人关节变量rnew的条件概率分布为

工业机器人在抓取观测变量为onew的物体时,通过驱动使得工业机器人的各个关节变量达到那么此时机器人就可以以最大概率完成对待抓取物体的抓取操作,实现对机器人抓住的有效控制。

2 试验验证分析

2.1 试验配置

试验所选择的机器人为UR3 机器人,属于小型的协作式桌面机器人,在轻型装配作业和自动化作业台上具有十分广泛的应用,机器人形状如图2 所示。获取待抓取物体观测变量的相机在UR3 机器人工作空间的上方,所选择的待抓取物体是一个立方体木块。对检测到的立方体木块边缘坐标进行平均获得立方体木块中心的坐标x、y。为了反映待抓取立方体木块的姿态,取立方体表面的一条边来计算立方体木块和相机横坐标轴的夹角θ,即待抓取物体的位姿观测变量为(x,y,θ),具体如图3 所示。

图2 UR3 机器人

图3 待抓取物体位姿

2.2 数据获取及模型训练

为了获取训练样本集,将立方体木块放置在工作区域内,通过UR3 机器人上方的相机来获取木块的位姿观测变量,同时拖动UR3 机器人去执行木块抓取,将木块的位姿观测变量和对应的UR3 机器人的关节变量记录,作为训练样本集中的一个样本。采用同样的方法重复上述木块抓取动作50 次,确保每一个木块在不同的位置,最终得到包含50 个样本的训练样本集。对获得的包含50 个样本的训练样本集,采用EM 算法对正态混合分布模型进行训练,最终将训练样本集划分为多个子集。对于每一个子集均服从正态分布,其对应于整个工作区域内的一个子区域。由于留一法(LOO)不受随机样本划分方式的影响,因此本文采用LOO 进行交叉验证,最终获得聚类的个数为4 个。用c1、c2、c3和c4表示4 个聚类中心,聚类中心的观测数据如表1 所示。

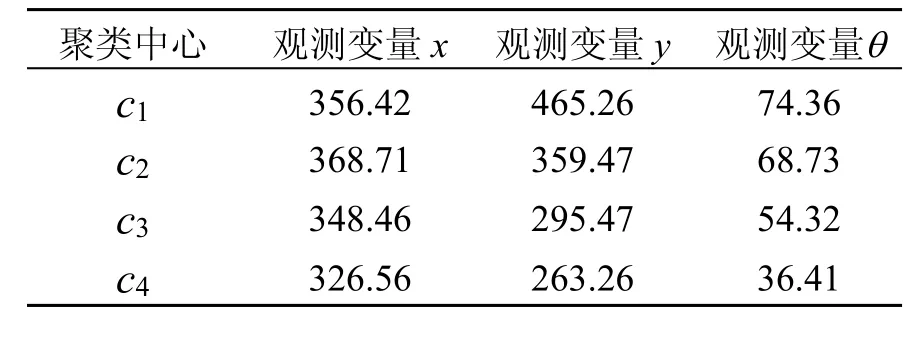
表1 4 个聚类中心观测数据

正态混合分布模型的参数为α1=0.251,α2=0.312,α3=0.289,α4=0.148。将立方体木块随意放置在工作平面上,UR3 机器人通过机器人上面的相机来获取该状态下立方体木块的观测变量(xnew,ynew,znew),同时计算观测变量(xnew,ynew,znew)在4 个正态分布中的后验概率。选择后验概率最大的正态分布来预测与之状态对应的UR3 机器人的关节坐标。根据该状态UR3 机器人的关节坐标去抓取立方体木块,具体如图4 所示。

图4 UR3 机器人木块抓取

2.3 结果分析

随机将立方体木块放置在工作平面不同的位置,使得立方体木块有不同的位姿,本文共对立方体木块20 种不同的随机位姿进行抓取试验,结果如表2 所示。

对UR3 机器人抓取立方体木块失败的位姿进行分析可知,抓取失败的位姿在样本训练集的边缘。为了对比基于EM 算法的正态混合分布模型由于单一的正态分布模型,将包含50 个样本的训练样本集,采用单一正态分布进行建模,同时对立方体木块20 种不同的随机位姿进行抓取试验,结果如表3 所示。

由表2 和表3 可知,采用单一正态分布模型对工业机器人进行抓取动作控制,其抓取的成功率比较低,同时通过对7 次抓取失败的分析可知,抓取试验的位姿在样本集的边缘和样本集的外部。

表2 混合正态分布模型20 次抓取试验结果

表3 单一正态分布模型20 次抓取试验结果

3 结论

抓取是机器人的基本动作,本文基于EM 算法对工业机器人抓取控制进行了研究。采用EM 算法的正态混合分布模型对训练样本集进行训练,获得了待抓取物体位姿观测变量和工业机器人关节变量之间的关系,通过数据驱动实现对机器人抓取控制。采用该控制方法对UR3 机器人抓取进行试验,结果表明基于EM 算法的正态混合分布模型能够更为准确地预测机器人关节变量,抓取成功率为95.0%。本文对减轻机器人操作者的工作负担以及提高机器人抓取成功率的相关研究具有一定的参考价值。