食品配料机器人调配咖啡流程运动规划

郑漫 ,金军

(1.安徽汽车职业技术学院 机电工程系,安徽 合肥,230601;2.合肥森曼智能科技有限公司,安徽 合肥,230601)

随着科学技术的发展,食品配料机器人技术的应用不断改善着人类生产生活,在工业领域广泛应用的机器人逐渐将人们从繁重的劳动中解放出来[1-3]。食品配料机器逐渐开始取代传统厨师,其为顾客带来了优质的服务和体验[4]。全自动食品配料机器人冲泡机可以在1 h 内冲出100 杯咖啡,相当于3 个咖啡师的产量。客户可通过应用程序订购的美味咖啡杯,同时可以控制配料、浓度、调味料和温度。

无论是在研究环境还是在工业应用中,食品配料机器人的路径规划都是一个具有挑战性的问题,特别是在高度动态的环境中考虑人机交互。在这种情况下,食品配料机器人研究的最终目标是为食品配料机器人提供在线、自主的运动规划。与许多机器人的运动规划方法相比,食品配料机器人机械手的方法假设环境是静止的[5-7],张延恒等[8]提出了以黎曼曲面上的测地线为依据进行操作臂与安装基座耦合状态下的空间机器人运动规划的方法,刘龙等[9]提出了根据不同的路径信息控制电机,进而调整小车速度和方向,最终实现小车沿设定路径行驶的方法。在路径生成之前需要离线估算障碍物,在离散化的食品配料机器人构型空间(C 空间)中生成子目标来指导规划路径,并行搜索有效路径。

本文以食品配料机器人的七自由度机械臂为实例,分析了机械臂的运动学正反解问题[10-11]。建立运动学模型对研究七自由度机械臂有很大的意义,有效验证了机械臂数学模型以及正解、逆解的正确性。在此基础上提出七自由度机械臂的规划器,其动态特性确保它可以处理静止、动态环境中的问题。

1 机械臂运动学建模

根据七自由度机械臂的机械结构,关节1、3、5、7 为旋转关节;关节2、4、6 为上升(或下降)关节。为了解决运动学冗余自由度复杂导致运动学多解,利用避障和轨迹算法来对机器人整体进行研究。

1.1 坐标系建立

将基座坐标系建立于S点(肩部)处,各个轴建立的坐标系相互之间关系如图1 所示(注意,在ROS零位时,L2与L3是共线的)。

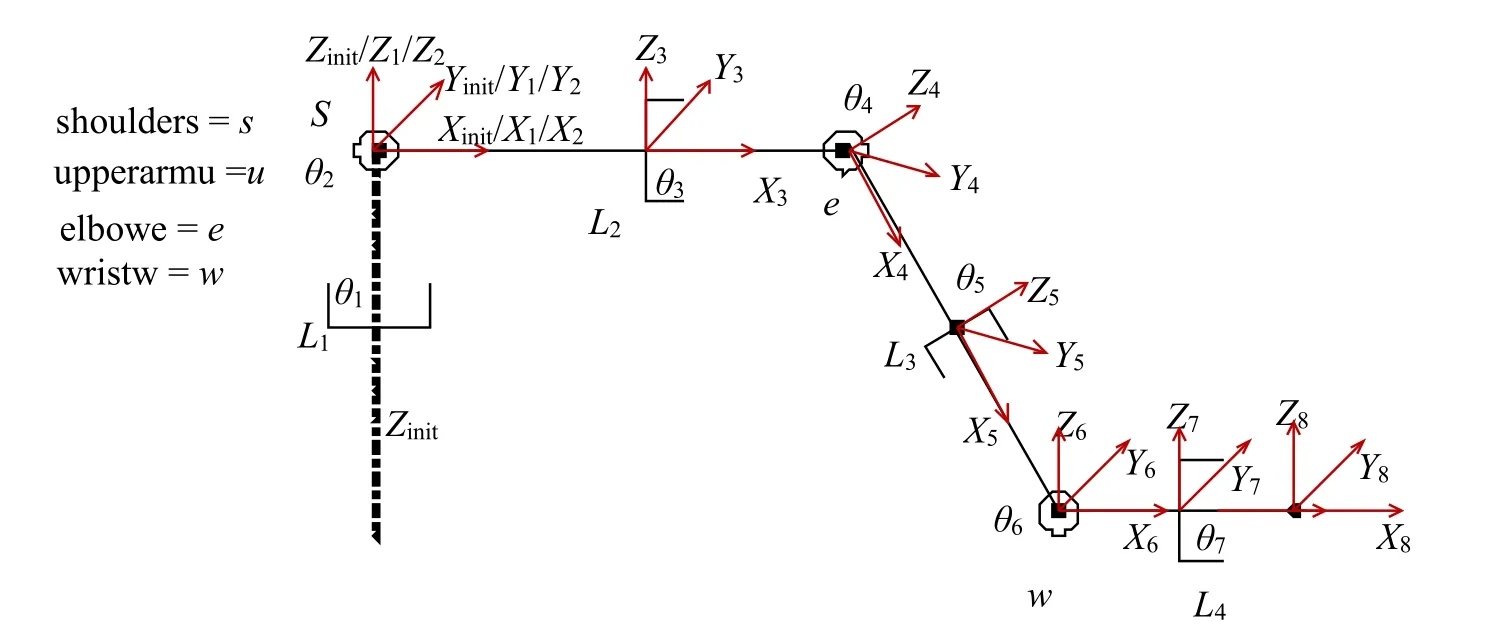
图1 7 自由度机械臂运动学坐标系分布

为描述方便,在下文中将关节n所对应的坐标系简称为坐标系n,将关节i的关节值记为θi,i=1,2,3,…,7。

关节1、2 和3的轴线相交于一点,交点与坐标系{1}、{2}和{3}的原点重合,关节轴1、2 和3 相互垂直。关节5、6 和7的轴线相交于一点,交点与坐标系{5}、{6}和{7}的原点重合,关节轴5、6 和7相互垂直。各个坐标系的建立方法如下:

(1) 坐标系1 与基坐标系的初始位置重合,并绕其Z轴转动,转动角度为θ1;

(2) 坐标系2 与坐标系1 初始位置重合并绕其Y轴转动,转动角度为θ2;

(3) 坐标系3 与坐标系2 初始位置重合并绕其X轴转动,转动角度为θ3;

(4) 坐标系4 相绕其Y轴转动,转动角度为θ4,并对于坐标系3的X轴正方向平移L2,平移向量为[L20 0]T;

(5) 坐标系5 与坐标系4 初始位置重合并绕其X轴转动,转动角度为θ5;

(6) 坐标系6 相绕其Y轴转动,转动角度为θ6,并对于坐标系5的X轴正方向平移L3,平移向量为[L30 0]T;

(7) 坐标系7 与坐标系6 初始位置重合并绕其X轴转动,转动角度为θ7;

(8) 坐标系8 相对于坐标系7 沿其X轴正方向平移L4,无转动。

程序默认的运动参数如表1 所示。

表1 食品配料机器人关节运动范围

续表1

1.2 运动学正解

通常把描述一个连杆和下一个连杆间相对关系的齐次变换叫做T矩阵。本文首先采用MDH 方法建立坐标系,进而用齐次变换矩阵来建立食品配料机器人末端执行器坐标系相对于基坐标系的数学模型。根据以上这些参数可以得到连杆坐标系之间的关系,同时获得各个关节之间的变换矩阵。

根据各个关节的空间几何关系可以获取到相邻两个坐标系的变换矩阵,如下所示:

总体正解为正确的运动学正解。

1.3 运动学逆解

将反向解析问题转化为只与前7 个坐标系相关的反向解析问题,下文所述中的“末端”如未做说明全部视为机械臂末端均为第7 轴末端而不是夹持器的末端,其向量的值即为第6 关节处质心的空间坐标。

由于7自由度机械臂的正向解析结果中涉及到7个关节值的正弦和余弦值,使用传统的反向解析方法,相当于处理一个七元七次方程组。因涉及到正弦与余弦,过高的次数会给计算带来极大障碍。分析7 轴机械臂的结构,容易得出反解会有无数组解,故ROS 采用一种新型的解法,逐步将各个轴的关节值解出。

1.3.1 反向解析第4 轴

机械臂的结构是以人类手臂为原型设计的,通过分析7 自由度机械臂的空间几何特点可以发现:当末端位姿与第4轴的关节值相对应,对于食品配料机器人的某一位姿,其各个关节值存在无数组可行解。第4 关节可行位置在空间中形成一个圆,圆面与第2 关节和第6 关节中心连线相垂直,各轴之间存在一定的几何关系。

1.3.2 反向解析第3 轴

第4 关节的位置可以位于一个圆周上,在所有的可行解中,第3 轴的关节值得取值范围覆盖了-180°～180°,故在不考虑机械限位的情况下,第3 轴可以任意取值,本算法中通常取值为第3 轴机械限位的中位数。

1.3.3 反向解析第2 轴

由于已经解出θ3、θ4,以此为基础来反向解析θ2,可做如下的处理:

机械臂的示意图如图2 所示。为便于直观理解,对图中几何关系进行说明,保持第4、5、6、7 轴关节值不变,转动第3 轴,可以形成如下图所示的一个圆周。取G、S、e3 点形成的平面(平面A′、B′、C′、D′垂直于水平面)为研究对象,点w′为点w在该平面上的投影,点w′与点w的Z轴坐标相同的。

图2 各轴几何关系示意

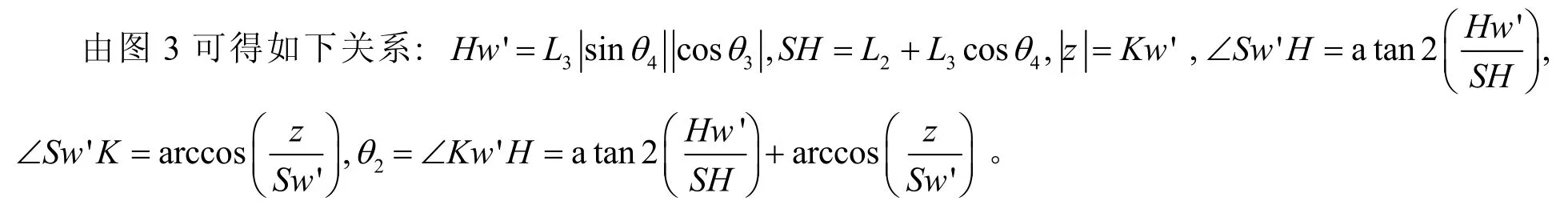
上述分析只考虑θ3及θ4＞0的情况,采用几何关系求解需要分别讨论θ2、θ3及θ4的多种情况,计算过程相关比较繁琐,因此采用运动学逆解的方式进行计算。

1.3.4 反向解析第1 轴

1.3.5 反向解析第5 至7 轴

反解前4 轴主要借助于末端位姿矩阵的p向量,而反解第5 至7 轴只需使用末端位姿矩阵中的n,o,a3 个向量。由坐标变换规则有如下关系:已知末端位姿矩阵,相当于已知同时由于上文已经解出前4 轴关节值,相当于已知将上式两侧同时乘以可得如下关系:

由于反解第5 至第7 轴只需使用n,o,a3 个向量,故上式可以简化为只做旋转矩阵的乘法,忽略平移向量,即其中由于为单位正交阵,故有如下关系:

至此,已将7 个轴的关节值全部得到反向解析。

2 分布式动态路径规划

尽管食品配料机器人调配咖啡师具有上述优点,但食品配料机器人咖啡店要完全取代传统的咖啡店还存在一定的争议。尽管AI 有所进步,但食品配料机器人并不能像人类一样善于区分口味的微妙之处。由于食品配料机器人与环境的实时交互,其规划系统必须能够在在线和动态的方式中获取关于障碍物的信息。

目前还没有能够动态集成障碍物信息的高维规划问题的实时解决方案,神经网络已被证明能够有效地解决多达3 维的高维规划问题。这促使将最初的6D 规划问题分解为2 个3D 问题,2 个3D 规划都涉及共同的现实环境限制,使得计划者的障碍景观不得不依赖于其它当前配置。

图3 所示工作空间内的圆形障碍物在角空间中诱导出不同的障碍物构型,其具体取决于实际的末端执行器在笛卡尔空间中的位置。手臂的当前方向分别由黑色箭头和字母C表示。这里将三维构型空间分解为二维位置空间和一维角度空间,分别表示末端执行器的笛卡尔位置和姿态。如果从灰色箭头所示的角度空间来看,位置空间中显示的3 种构型会导致不同的障碍物构型。当观察图中额外显示离散角轴时,禁止区域在角空间中的位移变得明显,其中禁止角配置用x标记。反之,禁止末端执行器在二维笛卡尔空间中的位置随着末端执行器的方向变化而变化。

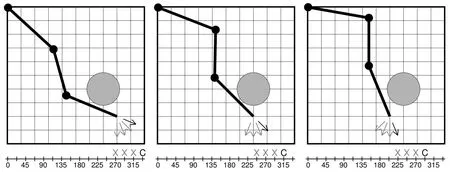
图3 工作空间内的圆形障碍物在角空间

3 实验和结果

3.1 仿真验证

用螺旋线生成一条机器人位置轨迹曲线将机器人的位置值输入到运动学求解器,通过逆解求出的一系列关节值。将关节值通过运动学求解器,通过正解求出一系列位置轨迹。将螺旋线生成的轨迹与运动学正解求取的位置轨迹进行比较,如图4 所示。

图4 中蓝色曲线代表规划的螺旋线,红色曲线代表用反解求出的关节值通过运动学正解求解出的位置螺旋线,从图4 可知,两条曲线处于重合状态,证明了机器人运动学计算的正确性。

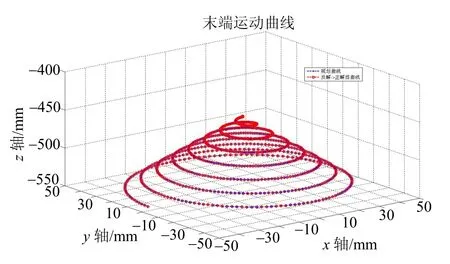
图4 正反解程序验证对比

3.2 实物验证

根据咖啡的调配流程和机器人运动学进行了如图5的实验流程。

图5 机器人制作咖啡流程

食品配料机器人非常擅长以完全相同的方式处理事情。三叶草倒立的圈子完全相同,其是在实验室中的无数实验确定的节拍节奏,因此计时非常精确。咖啡师所要做的就是提供正确剂量的新鲜磨碎的咖啡,确保将其正确分配在过滤器中,然后按一下按钮,机器完成其余的工作。自动化咖啡站提供快速智能的服务,无需全天候的人工干预即可为客户提供愉悦的体验。

4 结论

本文提出了一种7 自由度轻量化关节的机器人手臂。针对机器人本体结构特性对机器人选定坐标系,以轻量一体化关节食品配料机器人的七自由度机械臂为实例,利用球坐标获得正逆运动学方程。同时设计了一款规划器,结合末端执行器位置和方向的两个部分。路径规划算法专为高度动态环境下的路径生成而设计。测试结果表明,求解机械臂各个轴的顺序依次为θ4、θ3、θ2、θ1,在每个步骤中都可能存在多个符合条件的角,因此导致最终解出多组解,可以根据机械限位的情况筛选掉不在此范围内的解。