基于光锥结构的红外厚度传感器研究

郇 帅，莫长涛，文晶姬，吕 加，王 明，李 楠(哈尔滨商业大学 基础科学学院， 哈尔滨 150028)

红外厚度在线检测是一种非接触式的厚度检测方法，它采用单色红外光源将特定波长的多束红外光轮流照射到高速移动的待测样品上，利用样品各种组份对红外光源不同的吸收特性，对收集到带有不同厚度信息的光信号进行运算处理，获得厚度测量值[1].在红外厚度检测系统中，系统最佳参量如何优化选取，如红外光源供电电流及供电频率成为厚度检测的关键技术.为解决上述问题，本文建立理论模型并利用生物地理学优化算法进行多参量系统优化，建立输出功率与样品厚度、供电电流及供电频率的理论模型[2].

目前，国内厚度测量方法一般采用红外吸收法，常用于塑料薄膜厚度光学测量领域.红外光源发出一定功率的光信号，通过光学透镜组准直后由光电探测器接收，携带厚度信息的光功率部分损耗，同时传感器长期工作会造成光学系统偏差及玷污，影响测量精度，增加了仪器的造价与维修成本.为解决上述问题，本研究中采用俄罗斯单色红外光源，设计制作光锥，无需透镜即可实现对光线的会聚与准直，合理设计光锥参数，使携带厚度信息的光信号经高反射率多次反射后由光电探测器探测，解决了光路结构复杂[3]，降低了仪器生产及维修成本，可广泛应用于工业生产.

1 模型建立及算法

1.1 比尔-朗伯定律

一束单色光照射于吸收介质表面，在通过一定厚度的介质后，由于介质吸收了一部分光，透射光的强度就要减弱.吸收介质的浓度愈大或介质的厚度愈大，则光强度的减弱愈显著，其关系为

P=P0e-αcl

(1)

其中：P0为入射光的强度；P为透射光的强度；α为吸收系数；c为吸收物质的浓度；l为吸收物质的厚度；式(1)为比尔-朗伯定律的数学表达式[4].

固体材料的吸收系数是随入射光波长而变化的，其他因素对其影响较小，选择对应吸收波长的单色红外LED光源，待测样品材料浓度均匀且为常数，若用已知标准厚度的材料标定吸收系数后，可实现对样品未知厚度的检测.

1.2 模型建立

根据比尔-朗伯定律，传感器系统输出电压U与样品厚度d呈指数衰减关系；系统输出电压U与输入光强成正比，输入光强的大小由工作电流I决定，因此，输出电压U与工作电流I呈线性关系；系统输出电压U与光源频率的关系较为复杂，实验曲线如图1所示.

图1 不同供电电流下输出电压与供电频率之间的关系

在供电电流一定时，输出电压随着供电频率的变化先增大后减小，输出电压有一最大值Umax,此时对应的频率为f0，在f0左侧f与U近似呈幂函数关系；在f0右侧f与U近似呈指数衰减关系.即为最佳功率选择的依据.

根据实验结果，输出功率由三个参量决定，即样品厚度d、光源频率f和工作电流I.结合厚度传感器系统中各物理量的物理意义及关系，可以进行曲线拟合来确定样品厚度输出功率的数学模型.厚度传感器输出功率由输出电压U表征，是测量样品厚度的最终读取结果，是传感器系统中各关键参数的最优值确定的基本依据.因此，确定传感器系统输出电压与各主要输入参量的数据关系，是实验结果与物理意义相吻合的重要依据.根据光电探测器的基本特性，系统输出电压U与输出光强P成正比，可作为输出光强的结果度量，该结果与传感器系统输入光脉冲的基本参量有关，而传感器系统输入光脉冲的强度与输入电流成正比，光脉冲的频率与光源调制频率相同.因此，固定光源与光电探测器之间的距离，结合光吸收的基本物理过程与实验数据，构架本实验中的基本数学模型如式(2).

(2)

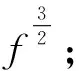
1.3 生物地理优化算法

Biogeography-based optimization(BBO),即生物地理学优化算法.是2008年被首次在IEEE上提出来的，作者是Dan Simon.它是研究生物的地理分布数学算法在最优化问题中的应用，和其他基于生物学的算法相比有很多共性，也有其独一无二的特性.它是在遗传算法和粒子群算法的基础上发展来的.适用于解决高维度的、多目标的最优化问题.考虑到迁入率曲线如图2所示，设该栖息地最大可能的迁入率为M，当该栖息地的物种为零时取最大值.随着物种的数量增加，栖息地变得更加拥挤，能够成功迁入该栖息地生存的物种减少，同时迁入率不断降低，该栖息地可以承受的最大物种数量为Smax，与此同时迁入率变为0.因此，可利用该优化算法去辨识复杂系统的模型参数解决厚度传感器的最优参数选择问题[7].

图2 生物地理优化算法原理图

利用生物地理学优化算法的优化途径可以对厚度传感器输出最佳功率进行优化计算，通过BBO算法在50次迭代中或得最佳功率，表明BBO算法对厚度传感器解决最佳输出电压优化问题的可行性[8].确定输出电压在测量高灵敏度状态下的系统影响系数为a1=3.25×10-3，a2=3.98×104，a3=0.001 13，该模型边界条件为f：30～1 024 Hz；I：137.8～187.4 mA，通过BBO算法并将模型初始条件与边界条件代入计算，可确定厚度传感器系统最佳输入参数应为f0=340 Hz，I=187.4 mA.该结果与模型边界条件基本吻合，可以说明实现高灵敏度测量本实验所确定的测量系统输入参数值基本合理.

2 光锥设计

光锥是一种圆锥体状或棱锥体状的聚光元件，是利用光线折反原理将光线进行聚集与传输.使用时将大端面放在光学系统的聚集面附近聚集光束，利用锥形内壁的高反射特性，在光锥内壁进行多次反射，将光线反射到小端面输出并由光电探测器接收，以达到提高单位面积光功率的目的，是一种非成像聚光元件[9].

对于红外光源厚度传感器而言，在满足高灵敏度检测要求的前提下，要达到空间短小，大视野角的光功率聚集，同时又希望使用尽可能小的红外光电探测器，实际上就是希望系统有尽可能小的等效F数[10].在传统的红外厚度传感器系统中，所需要的光学镜片多且结构复杂，成本偏高，而利用光锥使系统的等效F数减小，由于它独特的性能及造价低的特点，近年来被广泛应用于红外跟踪、辐射测量、水下选通等领域[11].

2.1 光锥设计原理

一个圆锥光锥，其介质折射率为n1，空气折射率n=1，入射端面宽为2H，接收端面为2R，α为光锥半顶角，θ为入射光线与光锥端面的入射角，β为入射光线与光锥光轴的夹角，L为光锥长度，则有：

L=(H-R)/tanα

(3)

假定光锥内壁反射时都为全反射，光线从大端面进入后经多次反射从小端面出射，根据反射定律，光线从大端面入射后，每反射一次后的入射角减小2α，则n次反射后的入射角为

θn=90°-[θ+(2n-1)α]

(4)

对应的

βn=θ+2nα

(5)

可知光线能继续向前传播的条件为：βn=θ+2nα<90°.光锥设计的原则是要保证单位面积上能量的聚集，由于反射次数的增加，能量递减，这对于能量采集系统很不利，所以需要尽可能的减少光线反射次数或增加光锥内表面的反射率，以尽可能的减少能量损失[12-13].见图3.

图3 圆锥光锥示意图

2.2 光锥设计制作

对比接收面上接收到的光功率，一次曲面、双曲面和抛物面光锥的出射总功率变化不大，一次曲面最高，抛物面最低.其原因在于到达接收面的总光线数不同，一次曲面曲率一致接收到的光线最多，反之双曲面和抛物面由于面型变化，根据反射定律部分光线折返出光锥无法使光线完全被光电探测器接收到.同时，材料缓慢氧化会使光锥内表面反射率逐渐降低，为使其保持较高反射率且不会由材料缓慢氧化带来反射率衰减，采用高、低折射率交替镀膜技术使光锥内表面反射率高达99%以上，如图4所示.这是因为从膜系各界面上反射的光束，当回到前表面时具有相同相位，从而产生相长干涉，获得高反射率，同时膜系材料在光锥基底上形成保护膜，可长时间保持高反射率状态[14-15].

图4 交替介质多层膜示意图

在固定光锥入射、出射端面尺寸的前提下，利用Light tools软件对光锥进行仿真设计与测试，得出设计方案：不同长度光锥聚光中心的位置不同，通过控制光锥长度可以控制聚光中心的位置，长度越长聚光性能越好.根据面型设计理论光锥参数如下：顶角20°，长度45 mm，入射端面直径10 mm、出射端面直径2 mm；应用Tfcalc膜系设计软件与高、低折射率交替镀膜技术，高折射率材料为Al2O3，低折射率材料为SiO2,在一次曲面光锥内表面制作共计48个膜层，实现了反射率高达99%，对光锥进行五次光功率检测，数据如表1所示.

表1 光锥检测参数表

数据表明，光源光功率经光锥n次折返后，光电探测器接收的光功率逐渐减小，这是由于光线在光锥中经多次反射后光功率衰减的累积所致，光锥内表面单次反射率平均值为99.36%，将实验数据回归方程，可计算出折返次数n=4.

3 实验结果

对红外厚度传感器采用双光束差分检测技术进行实验，将光路分为两路信号作比较，U1为检测光路输出电压，U2为参考光路输出电压.在厚度传感器最佳参数条件下，选取4片未知厚度的膜片进行测量，每片测量5次，与标准厚度进行比较，数据表如表2所示.

表2 厚度测量数据表

2.592.170.0885.462.592.140.0955.885.545.500.732.582.130.0945.792.572.150.0875.392.561.860.1589.652.551.850.1599.702.541.840.1609.749.819.850.412.541.800.17010.402.541.850.1579.582.531.550.24014.802.531.560.23714.612.531.570.23414.4214.5314.500.212.531.590.22814.032.531.550.24014.802.510.820.50833.802.510.840.49833.072.500.830.50233.3133.4733.250.642.500.840.49732.952.500.810.51034.05

4 结 语

实验数据表明：1)基于面型设计理论与高、低折射率交替镀膜技术制作了一次曲面光锥，可实现高反射率光线聚焦，其内表面反射率最高达99.45%，防止了基底缓慢氧化引起的反射率衰减从而影响测量精度，代替透镜组实现厚度传感器光路的准直，减少了光信号的损耗，解决了光学镜片结构复杂且成本高的问题.2)应用生物地理学优化算法解决了红外厚度传感器模型中参数优化问题，实现了厚度传感器数学表达式的建立与应用，能够实现对多种环境参量、非稳态参量优化选取，基于1)、2)技术研制的红外厚度传感器对膜片厚度测量，其相对误差最大值为0.73%，在厚度传感器制作行业领域中具有重要的意义.