广义双曲模型下锁定期权的定价
何二倩,李翠香(河北师范大学 数学科学学院, 石家庄 050024)
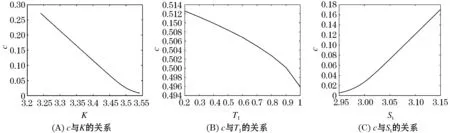
国际金融市场不断发展,标准期权已经不能满足投资者的需要,于是许多经济学家开始把目光聚焦到奇异期权上.锁定期权是一种路径依赖型奇异期权,它介于美式期权和欧式期权之间,期权的到期收益不仅与资产到期价格有关还与某一锁定时刻有关.假设t为当前时刻,T1为锁定时刻,T为期权到期日,t c(T,ST,K)=max(ST1-K,ST-K,0), p(T,ST,K)=max(K-ST1,K-ST,0). 2018年孙慧和李翠香[1]研究了带有信用风险的锁定期权的定价;2019年邱梓轩[2]研究了不完全市场下有违约风险的锁定期权的定价.这些研究都基于股票价格服从几何布朗运动,但是在实际情况下几乎所有的资产收益均呈现出尖峰厚尾,波动率微笑等特征.于是学者们开始寻找能更好拟合收益率的分布.Eberlein[3]and Keller(1995)首次将广义双曲分布应用到金融中. Barndorff-Nislsen在研究广义双曲分布的过程中发现正态分布,方差-伽玛分布等是它的特殊情况.于是广义双曲分布开始在各领域广泛应用.目前关于广义双曲分布在期权定价中的应用大多研究的是普通欧式期权的定价问题[4-6].本文将考虑资产价格服从指数广义双曲Lévy过程时锁定期权的定价问题. 常用的期权定价方法有两种:无套利方法和风险中性方法.无套利的方法是通过构建无套利的投资组合,求出期权价格满足的偏微分方程,从而得出期权的表达式.风险中性定价方法的原理是:在风险中性测度下任何衍生品的价格都等于到期收益按无风险利率贴现的期望值. 1994年, Gerber和Shiu提出用Esscher变换的方法寻找风险中性测度进而对期权进行定价[7]. 2018年, 李文汉,刘丽霞等研究了基于Esscher变换跳扩散模型下交换期权定价[8]. 2020年, 王梦娜利用Esscher变换寻找风险中性测度进而研究了幂期权的定价问题[9]. 同年, 李文汉,李翠香等研究了基于Esscher变换的外币期权定价[10]. 定义1.1[11]如果在概率测度P下随机变量X的密度函数为: (1) 其中:δ>0,|β|<α,λ,μ∈R Kλ(x)表示第三类修正Bessel函数,则称X在P下服从参数为α,β,δ,μ,λ的广义双曲分布,记作XP~GH(α,β,δ,μ,λ). φX(u)=Ep[eiuX]= (2) 其中:Ep[·]表示在概率测度P下的期望,i表示虚数单位.当u∈(-α-β,α-β)时,X的矩母函数存在且 MX(u)=Ep[euX]= (3) 定义1.2[11]测度P下参数为α,β,δ,μ,λ的广义双曲Lévy过程{Xt}t≥0是满足下列条件的随机过程 (i)X0=0; (ii) {Xt}t≥0具有独立平稳增量; 以后为了方便,用φt(u),Mt(u)分别表示Xt在测度P下的特征函数和矩母函数.φ(u),M(u)分别表示X1在测度P下的特征函数和矩母函数.由定义1.2中的条件(ii)知φt(u)=φt(u),Mt(u)=Mt(u). 本文假设市场存在两种基础资产:无风险资产(货币市场账户)和风险资产(标的资产).假设无风险利率为r,标的资产支付连续股息,股息率为q.r,q都为常数.标的资产价格过程{St}t≥0为带参数α,β,δ,μ,λ的指数广义双曲Lévy过程, 即 St=S0eXt, (4) 其中:{Xt}t≥0是参数为α,β,δ,μ,λ的广义双曲Lévy过程. 根据风险中性定价原理可知,为了求得期权的价格,关键是找出风险中性测度.下面利用Esscher变换的方法来寻找风险中性测度. (i)若X是关于Ft可测的随机变量,则 (ii)设Y是Ft可测的随机变量,则对0≤s≤t≤T有 其中:E[·|Ft]表示条件期望. 证明:对于任意的0≤s≤t≤T,因为Xs关于Fs可测,Xt-Xs与Fs独立,且与Xt-s分布相同,所以 证毕. S0=E[e-(r-q)tSt;θ], 其中:E[·;θ]表示在概率测度Pθ下的期望.由式(4)及引理2.1得 所以θ是下列方程的解 r-q=lnM(θ+1)-lnM(θ) . (5) 引理2.3[4]第三类修正的贝塞尔函数Kλ(x)有如下性质 (i)Kλ(x)=K-λ(x); (ii)当λ>0时,有Kλ(x)~Γ(λ)2λ-1x-λ,(x→0), 其中:Γ(·)为Gamma函数. 证明:令 g(θ)=lnM(θ+1)-lnM(θ). 则由式(3)和引理2.3得 且g(θ)在(-α-β,α-β-1)上连续,故存在θ*∈(-α-β,α-β-1)使g(θ*)=r-q. 又因为 所以E[X1;θ]是关于θ严格递增的函数.于是 因此g(θ)在(-α-β,α-β-1)上是严格增函数,从而唯一性得证. 为了方便把θ*记为θ,把Pθ*记为Q,φ(u)和φt(u)分别表示X1和Xt在测度Q下的特征函数,则 φt(u)=EQ[eiuXt]=EP[eiuXtΛ(t)]= (6) (7) 由此可以看出{Xt}t≥0为Q下的服从参数为α,β+θ,δ,μ,λ的广义双曲Lévy过程. 引理3.1[13](i) 设随机变量X在概率测度Q下的特征函数为φX(u),则 (ii)若二维随机变量(X,Y)在概率测度Q下的特征函数为φX,Y(u,v),则 引理3.2[14]设X为任一随机变量,Z(t)=EQ[eX|Ft],则{Z(t)}t≥0是Q鞅. 引理3.3 若X,Y独立,X,Y的特征函数分别为φX(u),φY(u),则(X+Y,Y)的特征函数为φX+Y,Y(u,v)=φX(u)φY(u+v). 证明:由特征函数的定义及X,Y的独立性直接可得. 定理3.1 当资产价格服从参数为α,β,δ,μ,λ的指数广义双曲Lévy过程时,锁定看涨期权在t时刻的价格为 其中:τ=T-t,τ1=T1,τ2=T-T1,φ(u)由式(7)给出. 证明:利用风险中性定价原理可知锁定看涨期权在t时刻的期权价格为 c(t,St,K)=e-r(T-t)EQ[max(ST1-K,ST-K,0)|Ft]= e-r(T-t){EQ[(ST1-K)I{ST1>K,ST1>ST}|Ft]+ EQ[(ST-K)I{ST>K,ST>ST1}|Ft]}, (8) 其中:I{A}表示集合A的示性函数. 令X=XT1-Xt,Y=XT-XT1则X,Y独立,且 ST1=SteX,ST=SteX+Y. 又因为St关于Ft可测,X,Y,X+Y都与Ft独立,于是 (9) 为了确定期权的价格公式我们需要计算(9)式右边的四项. 先计算第二项中的期望.由式(6)可知随机变量X,Y在Q下的特征函数分别为:φX(u)=φT1-t(u),φY(u)=φT-T1(u).又因为X,Y独立,于是二维随机变量(X,Y)在Q下的特征函数为:φX,Y(u,v)=φT1-t(u)φT-T1(v).由引理3.1得 (10) 同理,利用引理3.1,引理3.3得第四项中的期望 (11) EQ[Λ1(T)]=1, Λ1(u)=e-(r-q)(T1-t)eX,T1≤u≤T. (12) 由式(12)及引理3.1得 (13) (14) 将式(10)、(11)、(13)、(14)代入式(9)可得定理3.1.证毕. 类似于定理3.1的证明可得以下定理. 定理3.2 当资产价格服从参数为α,β,δ,μ,λ的指数广义双曲Lévy过程时,锁定看跌期权在t时刻的价格为 p(t,St,K)= 其中:τ=T-t,τ1=T1-t,τ2=T-T1,φ(u)由式(7)给出. 根据第三节中给出的锁定看涨,看跌期权的价格解析式,分析期权价格与执行价格,锁定时间,资产价格之间的关系. 文献[15]根据1997年1月2日~2003年9月19日期间共1616个交易日的上证综指日对数收益率,利用极大似然估计法得到的参数估计值为: λ=-0.989 9,α=26.936 3,β=-1.178 9, δ=0.014 8,μ=0.000 6 利用以上参数求解方程(5)得θ≈22.223 9. 根据华夏基金网站(http://www.chinaamc.com/fund/510050/lishifenhong.shtml)披露的历史分红数据,计算可得股息率q=0.018 3,取无风险利率r=0.017 4,以2020年12月23日的收盘价作为股票在t时刻的价格,即St=3.491,并取τ=1,τ1=0.5,K=3. 以下讨论当上述某因素发生变化,而其他因素不变的条件下,期权价格的变化.图1分别给出了锁定看涨期权在t时刻的期权价格c与K,T1,St之间的关系.可以看出c关于K是严格递减的;关于T1是严格递减的;关于St是严格递增的.图2分别给出了锁定看跌期权在t时刻的期权价格p与K,T1,St之间的关系.可以看出p关于K是严格递增的;关于T1是严格递增的;关于St是严格递减的. 图1 c与K,T1和St的关系Figure 1 Relationship between c and K, T1,St 图2 p与K,T1和St的关系Figure 2 Relationship between p and K,T1,St, 本文用风险中性定价方法讨论当资产价格服从广义双曲Lévy过程时锁定期权的定价问题.首先给出资产价格服从的广义双曲模型,用Esscher变换的方法找出风险中性测度.然后,再根据风险中性定价原理,利用测度变换以及分布函数和特征函数之间的关系得到锁定看涨,看跌期权的定价公式.最后对锁定看涨,看跌期权定价公式进行敏感性分析,得到锁定看涨,看跌期权价格与执行价格, 锁定时间,资产价格之间的关系.1 资产价格模型
2 风险中性测度
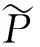

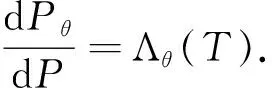
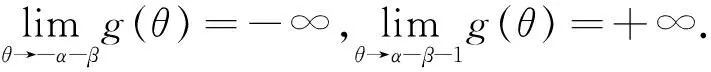
3 锁定期权的定价公式
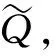
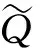
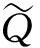
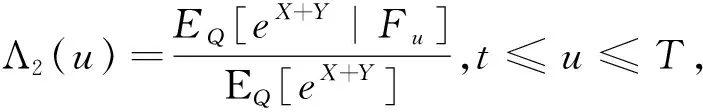
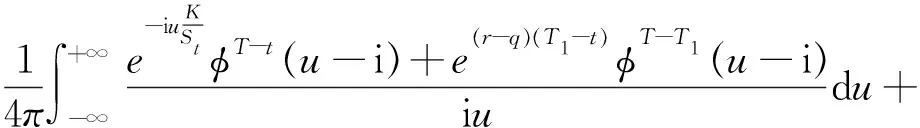
4 数值分析

5 结 语

