高密度椒盐噪声图像恢复方法的研究

马晓剑， 李梦娜， 邱奕萌， 孙丽雯， 谢之昱(东北林业大学 理学院，哈尔滨 150040)

图像作为人类进行信息获取和信息交换的主要来源，与人类的生活息息相关.然而，在图像获取和图像信号传输的过程中，噪声极大地影响着图像的质量，进而影响人类后续对图像的理解和处理.在众多噪声中，脉冲噪声最为普遍，它也被形象地被称为椒盐噪声.

至今为止，脉冲噪声的消除一直受到国内外学者的广泛关注.中值滤波及其改进算法运用非线性的方法平均地将每一处目标像素替换成周围像素强度的中值，随着噪声密度的增加，无法保留图像边缘，会产生条纹现象[1-3].同时高密度噪声下的中值极大可能也是噪声，导致滤波失效.DBA、NSBMF、BDND噪声检测及其改进算法运用脉冲噪声的极值性质，将检测窗口内的像素升序排序后进行噪声点的判别，但是在80%以上噪声浓度下这些方法会错误地将噪声点当作修复值，从也而产生条纹现象[4-6].UTMF、MDBUTMF提出了有效像素点的概念，运用排除修复窗口内全部噪声点的方法提高了滤波性能，但是当修复窗口都是噪声点时，滤波失效[7-8].

针对上述方法在高密度噪声下的弊端，本文利用D-S证据理论将信息融合技术应用到噪声检测中，提出了的自适应噪声检测方法，同时使用脉冲噪声的极值准则和不连续准则进行噪声点的判断.仿真实验结果表明，本文方法有效解决了高密度噪声条件下的滤波弊端，显著提高了滤波效果.

1 噪声模型与D-S证据理论

本文选用BDND算法文献[6]中的噪声模型，当8位灰度图像被脉冲噪声污染后，噪声点等可能的出现在两端宽度为l的取值范围内，此模型的概率密度函数为：

脉冲噪声主要具备两个性质：极值性和不连续性.极值性体现在噪声点的像素值往往是一个极大值255或极小值0，亦或是接近极值.不连续性体现在噪声点的像素值往往远高于或远低于周围像素值.对应这两个性质，两组判别准则应运而生，即极值准则和不连续准则，为同时使用两个准则进行噪点的判断，下面简要阐述D-S证据理论的融合规则.

概率指派函数是用来描述主观不确定现象的主要数学工具，它可以恰当的表示信息当中的“不知性”.对于某一问题，设其全部回答都属于集合Θ={θ1,θ2,…,θ1}，则Θ可被称为是该问题的识别框架，具有完备性和唯一性，其θi(i=1,2,…,l)中元素被称作焦元.若存在一个函数m∶2Θ→[0,1]满足[9]：

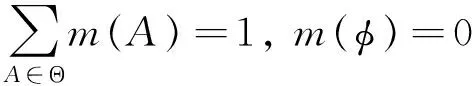
则称函数m为识别框架上的概率指派函数，m(A)描述了对焦元A的支持程度.利用两组概率指派函数，按如下方式进行信息融合[9]：

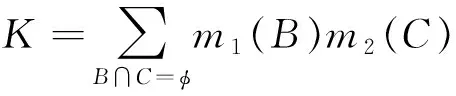
可传递信度模型(TBM)在要做出决策时使用Pignistic 概率转换得到Pignistic概率，将其概率分布记为BetP，可以以此概率分布进行决策.Pignistic概率转换(PPT)规则为[10]：

这里的|A|表示焦元A的势.

2 本文算法

2.1 噪声检测阶段

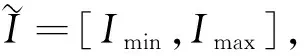
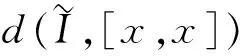
进而，利用上述定义的距离构造了一组概率指派函数m1，根据极值准则来判断待检测像素点是否被脉冲噪声破坏的不确定性[11]：

为避免分母为零，这里的β取0.1.

基于不连续准则，首先选用ROAD统计量[13]来描述这种不连续性质上的差异，定义d(xij,xi-s,j-t)=|xij-xi-s,j-t|表示待检测点xij与周围像素点xi-s,j-t之间的距离，设在检测窗口内待检测像素点周围共有M-1个临近像素点，则有M-1个d距离，将其按递增顺序排序，第g个d距离记为Rg(xij)，则系数为n的ROAD统计量为：

对于待检测点xij，当其ROAD值较大时应视为噪声点，反之视为信号.由此来构造依据不连续准则的概率指派函数m2[11]：

2.2 噪声修复阶段

修复窗口大小初始化为3×3，当满足时Nu<1/2×(1-P)×M时，修复窗口以中心像素为中心向外所有方向扩大一个单位，并且满足窗口大小不超过预设的最大值.修复窗口大小的预设最大值借鉴文献[14]的噪声点强度划分见表1.

表1 噪声点强度分类表

其中：Nu为当前修复窗口内信号的数量，M为当前窗口大小，P为噪声的概率密度.修复窗口Xwindow内，各个非噪声点与中心像素的距离记为距离矩阵:

(1)

修复Xwindow窗口内各个非噪声点的像素值与非噪声点中值Yij的偏差:

(2)

其中：r和c为所求矩阵的横纵坐标，i和j为中心元素的横纵坐标，Yij为修复窗口内非噪声像素强度的中值.注意，dis是计算非中心点，非噪声点元素的相关信息，其余点都用0来占位.由距离矩阵，可以计算出校正系数D以及最终的替换元素Zij.

这样实则是为中值Yij添加一个校正量，校正量的正与负取决于大于或小于组成的数组距离中心像素的相关性大小，即是使得Yij参考噪声强度与空间关系的一种方式.下面给出示例，其中ω代表噪声点.见图1.

图1 原始图像和噪声比为0.6的噪声图像示例Figure 1 An example of an original image and a noise image with a noise ratio of 0.6

该修复窗口内信号为Nu={20,21,21,22,23,149,152,152,153,153}，该数组的中值Yij为86，由公式(1)和公式(2)可得距离矩阵和偏差矩阵,见图2.

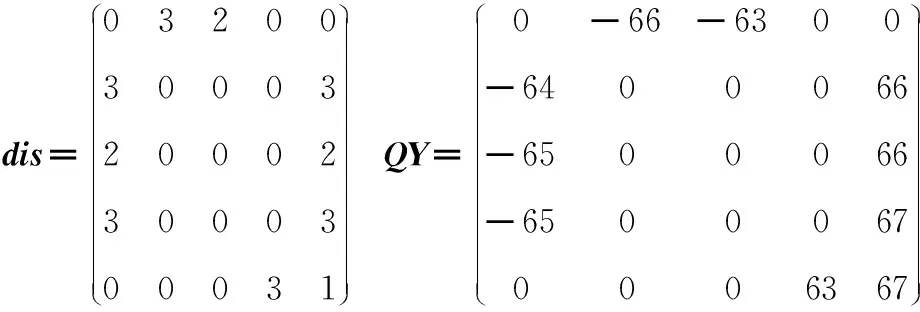
图2 距离矩阵和偏差矩阵的计算结果Figure 2 Calculation results of distance matrix and deviation matrix

最后计算修复值Zij为82，考虑了空间信息的偏移量更加接近真实值.

3 实验结果与分析

3.1 评价指标

为了更客观地评价本文提出的算法的有效性，我们利用了三个客观评价指标：峰值信噪比(RPSN)，均方误差(EMS)，和图像增强因子(FIE).计算公式如下：

其中：y为原始图像，x为被污染的噪声图，o为去噪之后的图象.M、N分别为图像的长和宽.

3.2 实验结果

本文使用的测试图尺寸均为512×512，它们分别是baboon图、pepper图、lena图和cameraman图.采用的对比算法主要有DBA、UTMF、NSBMF和MDBUTMF.

图3、4是噪声密度在40%和80%下各算法的修复图.可以明显地看出，在40%噪声密度下各个算法均有较好的修复情况，而随着噪声密度的增加，当噪声高达80%时，DBA算法出现较为严重的图像模糊现象，UTMF和NSBMF明显出现白色斑点，有大量噪声点未被有效识别.MDBUTMF算法图像信息缺失严重，处理结果难以识别.在高密度噪声条件下，对比算法均出现图像模糊、图像条纹以及图像信息大量缺失现象，而本文算法能够拥有明显的滤波效果，即使在细节和边缘处也可以保持大量的图像信息.

图5为标准图lena和cameraman的定量指标RPSN各个算法的对比，随着噪声密度的增加各算法的RPSN均呈下降趋势.对于lena图的RPSN指标值本文算法明显优越于对比算法，cameraman图在低密度噪声下除UTMF算法外，本文算法也优胜于其他算法，而在高密度噪声条件下，本文算法就显现出明显优势.

图5 标准图lena和cameraman的RPSN的对比Figure 5 Comparison of RPSN of standard graph lena and cameraman

表2为四张标准图的定量指标IEF和SSIM的数据对比，在噪声密度高达85%时，数据显示本文算法显著优于对比算法.

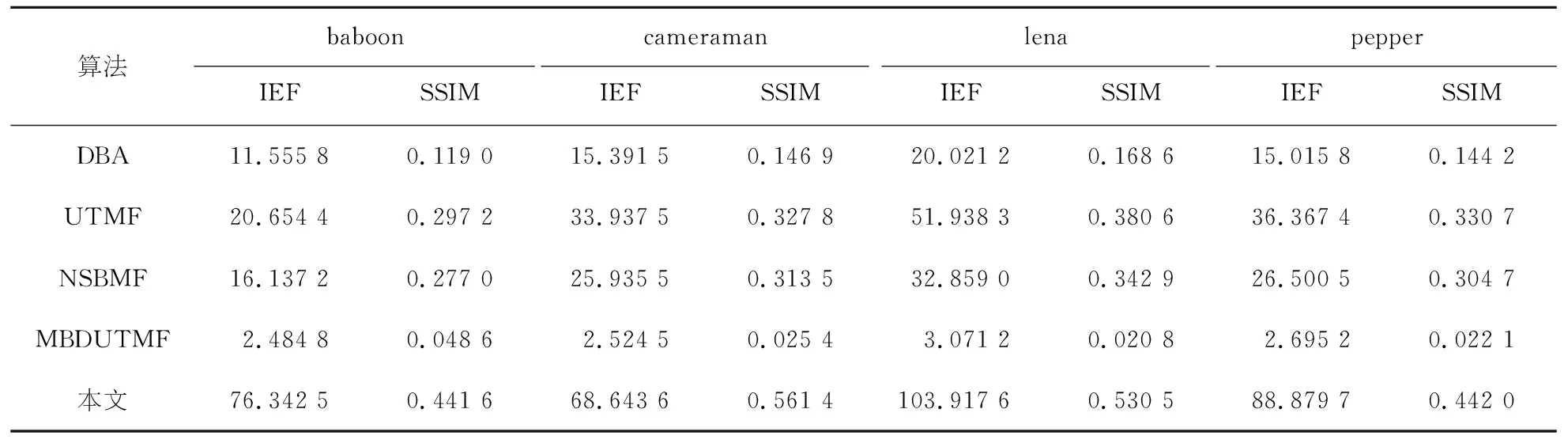
表2 四张标准图在噪声比为85%条件下的定量指标IEF和SSIM的对比

4 结 语

本文针对噪声检测方面，依据脉冲噪声的极值准则和不连续准则，利用D-S证据理论进行信息融合.在噪声修复阶段，对于检测窗口内非噪声点的中值，利用距离矩阵和偏差矩阵进行修正.D-S证据理论应用在图像处理方面是一个很好的思路，同时实验表明，在高密度噪声条件下，本文方法有很好的效果.但在噪声浓度达到85%以上的条件下，D-S证据理论存在高冲突的情况，有待进一步研究.