有限域2n上一类幂函数的差分谱及应用
满玉莹,夏永波(中南民族大学 数学与统计学学院,武汉 430074)
众所周知,密码学因其广泛的应用而备受关注. 密码函数是构成分组密码、序列密码和Hash函数等对称密码算法的重要组件,其密码学性质的好坏对该密码算法的安全性有着至关重要的影响,并且密码函数在通信和编码领域中也有着广泛的应用[1]. 近年来,如何设计S-盒来有效抵抗线性攻击和差分攻击是研究的热点. 差分一致性可以用来衡量密码函数抵抗差分攻击的能力,一个密码函数的差分一致性越小,其抵抗差分攻击的能力就越强[2-3]. 对于密码函数差分性质的研究,其中的一个课题就是计算密码函数的差分谱,差分谱从取值频次上对密码函数的差分分布表进行了刻画,在差分分析中可为寻找差分攻击路径提供依据. 由于具有较低差分一致性的幂函数在硬件实现方面更为便利,所以其通常被用于S-盒的设计中. 例如美国高级加密标准(AES)就是使用有限域28上差分一致性为4的Inverse函数x|→x-1来设计的[4]. 对于幂函数往往通过确定其差分谱来进一步刻画它的差分性质. 因此确定具有较低差分一致性幂函数的差分谱受到了国内外密码学者广泛的关注.
设n=4k,对于有限域2n上的幂函数F(x)=x22k+2k+1(该函数被称为Bracken-Leander幂函数),因为其具有较低的差分一致性和较高的非线性度,所以其受到了国内外学者的广泛关注. 2010年,BRACKEN和LEANDER首次在文献[5]中研究了F(x)的Walsh谱和差分一致性,证明了无论k是奇数还是偶数,F(x)都是4差分置换,并且分别得到了k是奇数和偶数时F(x)的Walsh谱. 对于F(x)差分谱的计算,BLONDEAU等人在文献[3]中利用平方和指标函数得到了F(x)的差分谱,但是该方法只适用于k为奇数的情况. 随后在2017年,XIONG、YAN在文献[6]中通过研究差分方程(x+1)22k+2k+1+x22k+2k+1=b的解数直接确定了F(x)的差分谱,他们的方法同时适用于偶数k和奇数k.
本文将提供一种新的方法求解F(x)的差分谱:利用BRACKEN和LEANDER在文献[5]中给出的该函数的Walsh谱,基于文献[7]中提出的差分谱和Walsh变换之间的关系确定了F(x)的差分谱. 该方法相比于文献[6]中所用方法更为简单. 利用F(x)的差分谱,确定F(x)的两个密码学指标ambiguity和deficiency的取值. 此外对于Kassami幂函数也计算了它的ambiguity和deficiency.
1 基础知识
设p为任意素数,n为正整数,pn是含有pn个元素的有限域并且pn{0}· 下面给出本文所需的基本概念·
定义1[3]设F(x)是从pn到pn的一个函数,则F(x)在(a,b)∈pn×pn处的Walsh变换定义为:
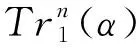
F(x)的Walsh谱定义为多重集ΛF={WF(a,b):a,b∈pn,a≠0}·
定义2[8]设F(x)为有限域pn到自身的映射,对于任意pn,定义差分方程ΔaF(x)=F(x+a)-F(x),δF(a,b)为ΔaF(x)=b在pn上解的个数,即:
δF(a,b)=|{x∈pn|ΔaF(x)=b}|,
其中|S|表示集合S的基数· 称矩阵(δF(a,b))a,b∈pn为F(x)的差分分布表· 令:
F(x)的差分一致性定义为δ(F)·
设F(x)为有限域pn到自身的映射,若δ(F)=k则称F(x)为k-差分一致性函数· 特别地,若δ(F)=1,则称函数为完全非线性函数(PN函数),若δ(F)=2,则称函数为几乎完全非线性函数(APN函数)· 对于特征为2的有限域,函数的差分一致性最低只能达到2,这是因为若x0满足方程F(x+a)-F(x)=b则有x0+a也一定满足该方程·
下面沿用定义2中的记号给出密码函数差分谱的定义,密码函数的差分谱是对其差分性质更精细的一种刻画·
定义3[9]设F(x)为pn到自身的映射,若F(x)的差分均匀度为k,则为F(x)的差分谱,其中:
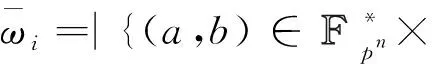
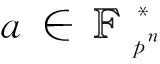
由此得δF(a,b)=δF(1,b/ad)· 也就是说幂函数F(x)的差分谱完全由δF(1,b)的值确定出来,其中b遍历pn· 令:
ωi=|{b∈pn|δF(1,b)=i}|,0≤i≤k,
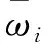
为了描述F(x)的差分函数ΔaF(x)=F(x+a)-F(x)的单射性和满射性,PANARIO等人在文献[10]中提出了两个新的密码学指标:ambiguity和deficiency. 利用定义3中密码函数差分谱的定义,下面给出ambiguity和deficiency的定义·
定义4[10]设F(x)为pn到自身的映射,F(x)的ambiguity定义为的deficiency定义为
A(F)是衡量F(x)的差分函数ΔaF(x)的单射性,并且F(x)的ambiguity越低,F(x)的差分函数ΔaF(x)越接近单射·D(F)是衡量F(x)的差分函数ΔaF(x)的满射性,并且F(x)的deficiency越低,F(x)的差分函数ΔaF(x)越接近满射·
若F(x)=xd是有限域2n(n≥2)上的一个4差分一致性函数,则对于A(F)和D(f)的界有如下引理·
引理1[11]设F(x)=xd是有限域2n(n≥2)上的一个4差分一致性函数,则有:
(2n-1)(2n-1+4)≤A(F)≤3·2n-1(2n-1),
(2n-1)(2n-1+1)≤D(F)≤3·2n-2(2n-1)·
设F(x)是从pn到pn的一个k-差分一致性幂函数,{ω0,ω1,…,ωk}为其差分谱,则幂函数F(x)有如下性质·
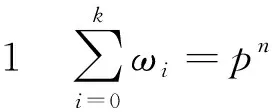
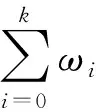
下面给出后续证明中用到的重要引理·
引理2[5]设函数F(x)=x22k+2k+1是定义在有限域2n上的一类幂函数,其中n=4k.则F(x)的Walsh谱由如表1和表2给出·

表1 当k为偶数时F(x)的Walsh谱Tab.1 The Walsh spectrum of F(x) when k is even

表2 当k为奇数时F(x)的Walsh谱Tab.2 The Walsh spectrum of F(x) when k is odd
(1)当k为偶数时
(2)当k为奇数时
对于幂函数F(x)=xd,文献[7]中给出了F(x)的Walsh谱和定义2中δF(a,b)之间的关系,借助这一关系,可以建立Walsh谱和差分谱之间的如下关系·
引理3 设F(x)=xd是pn到pn的一个k-差分一致性幂函数,{ω0,ω1,…,ωk}为其差分谱,WF(a,b)为F(x)在(a,b)∈pn×pn处的Walsh变换,则有:
证明由
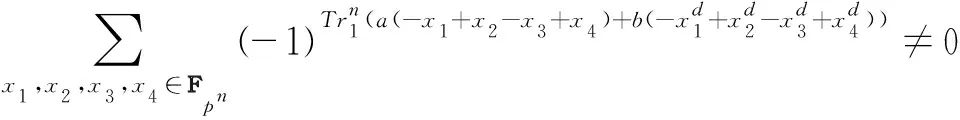
的解· 设u=-x1+x2=x3-x4则有x2=x1+u和x3=x4+u.因此有:
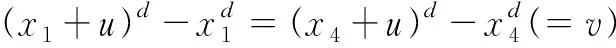
2 主要结果及证明
定理1 设F(x)=x22k+2k+1是有限域2n上的幂函数,其中n=4k,则F(x)为4差分一致性函数且差分谱为:
{ω0=5·24k-3-23k-3,ω1=0,ω2=24k-2+23k-2,ω3=0,ω4=24k-3-23k-3}·
证明对于有限域2n上的Bracken-Leander幂函数,BRACKEN和LEANDER在文献[5]中证明了F(x)为4差分一致性函数,设该函数的差分谱为{ω0,ω1,ω2,ω3,ω4}· 因为F(x)的差分方程(x+1)22k+2k+1+x22k+2k+1=b的解是成对出现的,所以有ω1=ω3=0,下面只需求得ω0,ω2,ω4的值·
由Walsh变换的定义知当a=0时容易得出:
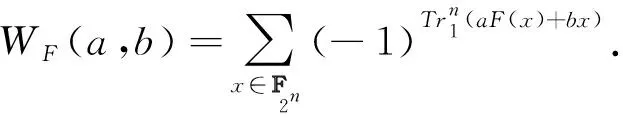
当k为奇数时可得:
进一步由引理3知:
24n+22n(2n-1)(4ω2+16ω4),
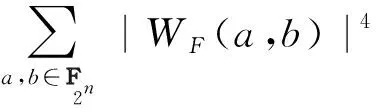
STEM教育与STEM职业的联系 教育的目的是为社会建设培养专业人才,对接社会的现代化发展。STEM教育理工科属性很强,从事社会建设的科技产业建设者需要具有此类的设计性思维,对于社会的科技产业具有很强的带动作用。
由此可得到F(x)的差分谱并且当k为偶数和k为奇数时F(x)的差分谱相同·
下面给出利用Magma软件计算实例所得到的结果·
例1 取k=2,n=8· 利用Magma软件,得到F(x)=x21在28上的差分一致性为4且差分谱为:
{ω0=152,ω2=80,ω4=24}·
例2 取k=3,n=12· 利用Magma软件,得到F(x)=x73在212上的差分一致性为4且差分谱为:
{ω0=2496,ω2=1152,ω4=448}·
以上求得的F(x)差分谱无论是数值结果还是理论结果都与文献[8]中所得结果是一样的·
3 两类幂函数的ambiguity和deficiency
利用定理1中给出的Bracken-Leander幂函数的差分谱,可确定该函数的ambiguity和deficiency.
定理2 有限域2n上Bracken-Leander幂函数F(x)=x22k+2k+1,其中n=4k.F(x)的ambiguity为A(F)=(2n-23k-1)(2n-1),F(x)的deficiency为D(F)=(2n-1)(5·2n-3-23k-3)·
证明由F(x)=x22k+2k+1的差分谱以及F(x)的ambiguity和deficiency的定义可得:
利用定理2中的结果,下面考虑F(x)=x22k+2k+1的A(F)和D(F)与引理1中上下界的接近程度·
设n,k为正整数,当gcd(k,n)=s且n/s为奇数时,称幂函数G(x)=x22k-2k+1为Kassami幂函数· 文献[12]中证明了G(x)的差分一致性为2s· 随后,BLONDEAU等人在文献[3]中确定了其差分谱为:
{ω0=2n-2n-2,ωi=0(∀i,2≤i<2s),ω2s=2n-2},
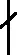
{ω0=2n-2n-2,ω2=0,ω4=2n-2},
定理3 有限域2n上Kassami幂函数H(x)=x22k-2k+1,其中n=2t,2t且gcd(k,n)=2.H(x)的ambiguity为A(H)=3·2n-1(2n-1),H(x)的deficiency为D(H)=3·2n-2(2n-1)·
证明由H(x)的差分谱以及ambiguity和deficiency的定义可得:
3·2n-1(2n-1),
D(H)=(2n-1)ω0=3·2n-2(2n-1)·
易见幂函数H(x)=x22k-2k+1的A(H)和D(H)达到引理1中的上界·
4 结论
近年来关于有限域上低差分一致性密码函数的研究已经取得了很多重要的结果,已有大量幂函数的差分一致性被确定出来,但仍有很多幂函数的差分谱尚未被确定. 本文基于Bracken-Leander幂函数Walsh谱的研究结果,利用差分谱和Walsh变换之间的关系,确定了Bracken-Leander幂函数的差分谱. 幂函数差分谱的研究,最终都会转化为求解有限域上一些方程的根的个数及其分布,对于差分谱未知的低差分幂函数能否找到一些新的求解方程的技巧是确定其差分谱的关键. 目前国内外学者对于有限域上密码函数差分谱的研究主要集中在少数几类幂函数以及次数不超过6的正规化置换多项式上,对于其他低差分一致性的密码函数能否确定出其差分谱,将是后续研究的问题.

