基于间歇牵制量化控制的耦合复杂网络有限时间同步

梅俊，李园园，杨占英，夏丹( 中南民族大学 数学与统计学学院，武汉 430074; 华中师范大学 人工智能教育学院，武汉 430079)

近年来，复杂网络同步问题的研究引起了广泛关注.同步包括有限时间同步[1]、指数同步[2]和渐近同步[3]等.其中，有限时间同步由于其快速收敛性在实际中有重要的应用.然而，在一些有限时间同步的研究中[4-7]，其系统的控制器是连续的，需要控制器持续工作，这就意味着成本会大大增加.

间歇控制方法作为经济实用的策略之一，能够节约大量成本[8].该控制方法将工作时间分为两部分:非零区间和其他区间，在非零区间工作，在其他区间关闭.为了更好地提高经济效益，牵制控制是一个很好的选择，因为只需控制部分节点.所以，间歇牵制控制一方面可以使系统更加简单实用，另一方面可以节约成本.另外，对信号进行量化可以减轻信道阻塞，加快通信效率[9].据作者所知，对于耦合复杂网络的间歇牵制量化的研究目前尚未见报道，所以研究基于间歇牵制量化控制的耦合复杂网络的有限时间同步具有重要的理论价值和实际意义.

1 模型描述与准备知识

考虑具有N个相同节点的耦合复杂网络模型，其节点动态方程描述如下:

(1)

其中N={1,2,…，N},xi(t)=(xi1(t),xi2(t),…，xin(t))T∈n表示第i个节点的状态向量，g(·):n→n为连续函数，A∈n×n是常值矩阵，Φ=(φij)N×N表示网络的外部耦合矩阵，满足对于i≠j有φij≥0,且是内部耦合矩阵，c>0为网络的耦合强度，设节点状态xi(t)的初值是xi(0),i∈N·

称方程(1)为驱动网络，响应网络的动态方程描述如下:

(2)

其中yi(t)=(yi1(t),yi2(t),…，yin(t))T∈n,ui(t)表示响应网络第i个节点的控制输入，其他参数与网络(1)中相应的参数表示相同，其初值为yi(0),i∈N·

定义(1)与(2)的误差系统的状态方程为:

(3)

其中zi(t)=yi(t)-xi(t),f(zi(t))=g(yi(t))-

g(xi(t))·

因此，将复杂网络(1)和(2)的同步问题转化为误差系统(3)的稳定性问题·

定义1 若存在一个常数t*>0使得：

并且对于任意t>t*都有‖yi(t)-xi(t)‖2≡0,若V(t)是径向无界的，则称耦合复杂网络(1)与(2)可以实现全局的有限时间同步·

假设1 函数g(x)满足Lipschitz条件，即存在一个常数d≥0使得：

‖g(y(t))-g(x(t))‖≤d‖y(t)-x(t)‖,

∀x(t),y(t)∈Rn·

下面给出4个必要的引理·

引理1[10]令η1,η2,…，ηN≥0,0<α≤1,β>1，则如下不等式成立:

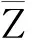
引理3[12]对于一个给定的实矩阵:

(i)S<0;

引理4[13-14]假设存在一个正定函数V(t),当t∈[0,+∞]时，满足以下条件:

其中，α,β>0,T>0,l∈,0<η<1,0<θ<1,则如下不等式成立:

V1-η(t)≤(V(0))1-ηe(1-η)β(1-θ)t-αθ(1-η)t,0≤t≤t*,

或者t*=T2,

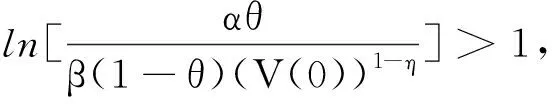
2 主要结果

设计如下间歇牵制量化控制器:

(4)

其中li>0为控制增益，ξ>0为协调常数，0<μ<1,T>0是控制周期，l=0,1,2,…,∞,0<θ≤1是控制比率，[φ(zi(t))]μ=([φ(zi1(t))]μ,[φ(zi2(t))]μ,…，[φ(zin(t))]μ)T,其中φ(·)∶→Ω是量化器，其中Ω={±ωi∶ωi=ρiω0,i=0,±1,±2,…}∪{0},ω0>0,对于任意τ∈R,量化器φ(τ)构造如下:

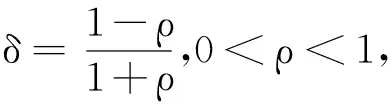
误差系统的简写形式如下:

(5)

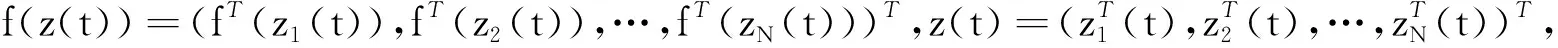
[φ(z(t))]μ=(([φ(z1(t))]μ)T,([φ(z2(t))]μ)T,…，([φ(zN(t))]μ)T)T,A=IN⊗A,Φ=Φ⊗Γ,L=diag(l1,l2,…,lm,0,0,…,0)⊗In,Λ(t)=diag(Λ1(t),Λ2(t),…,ΛN(t)),Λi(t)=diag(Λi1(t),Λi2(t),…,Λin(t)),Λij(t)是Filippov解，其中Λij∈[-δ,δ),i=1,2,…,N,j=1,2,…,n.

定理1 若假设1成立,ξ,β>0,给定控制增益L，如果存在正定对角矩阵P、正常数ε和ζ使得下列条件成立:

(6)

(7)

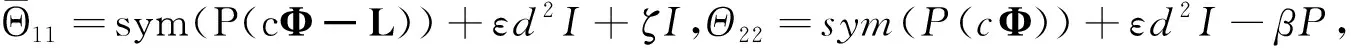
或

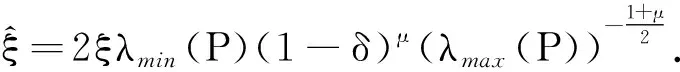
证明考虑下面的Lyapunov函数:

V(t)=zT(t)Pz(t)·

(8)

当t∈[lT,(l+θ)T],由(5)式可得:

ξ[φ(z(t))]μ]=zTPAf(z(t))+fT(z(t))ATPz(t)+zT(t)P(cΦ-L-LΛ(t))z(t)+zT(t)(cΦ-L-LΛ(t))TPz(t)-2ξzT(t)P[φ(z(t))]μ≤zT(t)PAf(z(t))+fT(z(t))ATPz(t)+zT(t)P(cΦ-L+δL)z(t)+zT(t)(cΦ-L+δL)TPz(t)-2ξzT(t)P[φ(z(t))]μ,

(9)

根据假设1，可得:

d‖zi(t)‖=d‖yi(t)-xi(t)‖≥g‖(yi(t))-g(xi(t))‖=‖f(zi(t)‖,

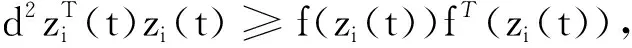
εd2zT(t)z(t)-εfT(z(t))f(z(t))≥0,

由(9)式可推出:

(10)

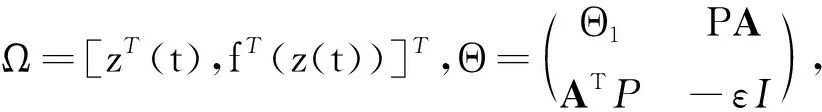
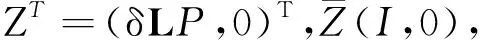
通过引理2、引理3和条件(6)可推导出:

故由(10)式可得:

(11)

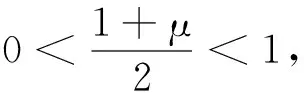
-zT(t)P[φ(z(t))]μ≤-λmin(P)zT(t)[φ(z(t))]μ=

(12)

根据(11)和(12)式可得:

(13)

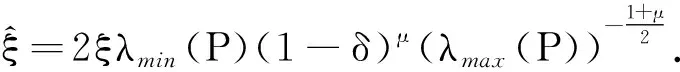
当t∈((l+θ)T,(l+1)T)时，由(5)式可得:

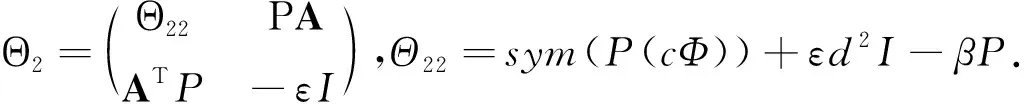
根据条件(7)可得:

(14)

证毕·

3 数值仿真

考虑误差系统(3)，其中A=diag(27/7,0,0),Γ=diag(1,1,1)激活函数f(x)满足f(z1(t))=(|z1(t)+1|-|z1(t)-1|,0,0)T,量化器密度ρ=0·7

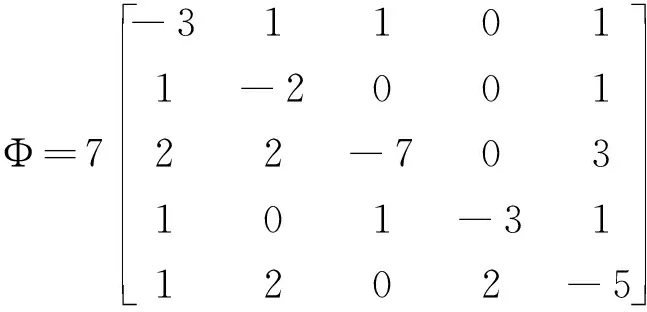
取控制周期T=0·1,控制宽度θ=0·5,耦合强度c=1,ξ=1,μ=0·5,β=16,假设1满足d=2,给定控制增益l1=20,l2=30,l3=15,l4=l5=0·

利用Matlab LMI工具箱求解(6)-(7)式得出

P=diag(0·0252,0·0252,0·0233,0·0283,0·0283,0·0267,0·0103,0·0103,0·0103,0·0275,0·0275,0·0276,0·0242,0·0242,0·0232),ε=0·0570,ζ=0·1491·

网络(1)和(2)的初值分别为:

x1(0)=[1,-1,0]T,x2(0)=[-1,2,1]T,x3(0)=

[1,0,1]T,x4(0)=[0,-1,1]T,x5(0)=[1,-1,1]T,y1(0)=[5,4,1]T,y2(0)=[-1,-2,1]T,y3(0)=

[3,2,4]T,y4(0)=[1,0,1]T,y5(0)=[0,1,2]T,zij(t)=yij(t)-xi(t)(i=1,…,5,j=1,2,3),图1给出不加控制器时误差动态系统的轨迹图，可以看出，如果不施加控制，耦合复杂网络(1)和(2)无法实现同步·图2描述了耦合复杂网络加入间歇牵制量化控制器之后的误差动态系统的轨迹图，由图2看出网络在有限时间内达到同步·图3是对信号进行量化后的误差系统轨迹图，可以明显地看出被量化的信号呈折叠线的状态·

图1 未加入控制器的误差系统轨迹图Fig.1 Trajectories of error systems without controller

图2 基于间歇牵制控制器的误差系统轨迹图Fig.2 Trajectories of error systems with intermittent pinning controller

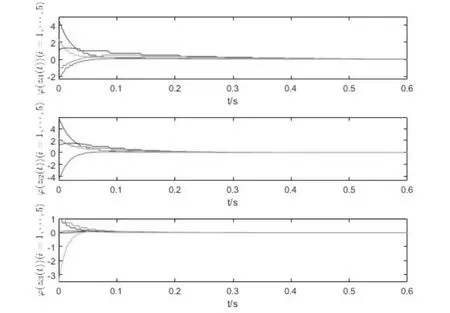
图3 ‖φ(zi(t))‖(i=1,…,5)的轨迹图Fig.3 Trajectories of ‖φ(zi(t))‖(i=1,…,5)

4 结论

对于耦合复杂网络的有限时间同步问题，不少文献已经进行了深入研究，但是，控制方法普遍采用连续控制.与其不同，本文研究的是基于间歇牵制量化控制实现耦合复杂网络的有限时间同步.首先，设计了一个间歇牵制量化控制器， 然后利用Lyapunov函数的性质和Schur补偿引理，得到耦合复杂网络的有限时间同步的充分条件.最后，通过数值仿真验证了其有效性.