立足核心素养解决圆锥曲线中的“定”问题——从一道圆锥曲线定值问题谈起

江苏省盱眙县兴隆中心小学 (211700) 史媛媛

1.问题呈现

(1)求椭圆C的标准方程；

此题来源于我校一份阶段试卷，参考答案如下：

2.结论初探及拓展

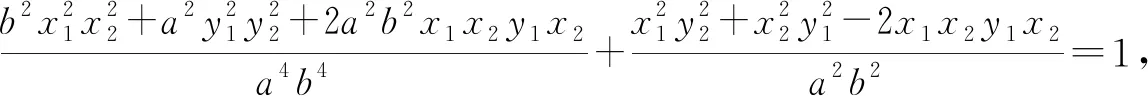
限于篇幅，结论3，4留给读者自行完成.

3.借题发挥

(1)求椭圆C的标准方程；

(2)试问：k1·k2是否为定值？若是，求出该值；若不是，说明理由.

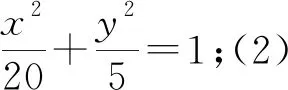
4.结语

探索圆锥曲线的定值问题常见方法有两种：①从特殊入手，先根据特殊位置和数值求出定值，再证明这个值与变量无关；②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值.解答的关键是认真审题，理清问题与题设的关系，建立合理的方程或函数，利用等量关系统一变量，最后消元得出定值.

数学的学习和研究从不满足于特殊情况的结果，而是通过归纳、类比等方法去探索、研究各种对象的一般规律，寻求解决问题的一般方法.在教学过程中，应引导学生熟悉数学命题的条件与结论之间的逻辑关系，通过一些重要命题启发学生探究该命题的多种变化形式及相互逻辑关系，真正地让逻辑推理逐渐成为数学教学中培养学生创新精神的重要方法.