寻求函数式大小关系的四种方法
2021-10-22 14:04:44南京师范大学附属中学江宁分校211102李中阳
中学数学研究(江西) 2021年9期
南京师范大学附属中学江宁分校 (211102) 纪 晖 李中阳
用导数解决两个函数式大小关系问题是导数的一个重要应用,在高考压轴题中也经常出现,由于涉及的知识点较多,解题过程也变化复杂,故而经常对同学们继续求解造成困难,本文通过典例的分析点评,介绍解决此类问题常见有四种方法,供读者朋友参考.
一、分别求最值
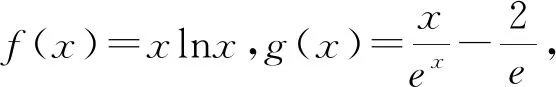
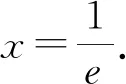
点评:如果能够确定两个在相同区间内的取最值情况,并且有相反的开口走向,选用此法确定两个函数的大小关系,是非常经济实用的.
二、作差后与0比较
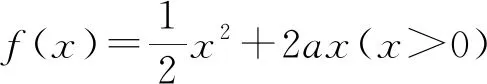
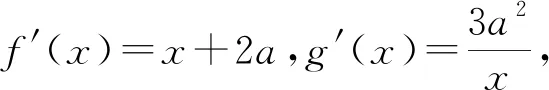
点评:如果不能由两个函数取最值的情况确定大小关系,通过对两个函数式作差,再求由此得到的新函数的最值,然后与0比较,就可以证明出这两个函数式的大小关系.
三、转化后再比较
例3 已知函数f(x)=xlnx-ex+1,h(x)=sinx.试证明:f(x) 点评:在直接采用分别求两个函数最值和作差求最值的方法不奏效的情况下,可以先对要证的不等式进行代数变形,通过分段分析、分别解决的方法确定大小关系. 点评:根据不等式的传递性,通过中间函数的桥梁作用,可使问题轻松解决,这就是转化解题的作用,其中的中间函数的选取非常重要,这是经验与智慧的体现.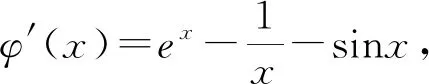
四、通过中间函数过渡
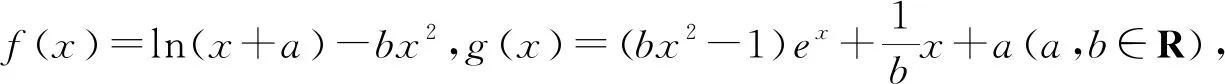
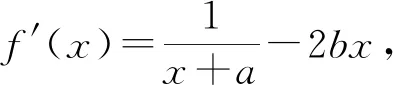
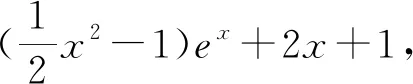
猜你喜欢
初中生世界·七年级(2022年6期)2022-05-28 14:02:01
江苏教育(2021年54期)2021-08-31 10:12:32
中小学校长(2021年7期)2021-08-21 06:49:56
科教导刊·电子版(2020年2期)2020-05-11 05:54:15
小学生作文(低年级适用)(2019年10期)2019-10-28 06:46:26
课程教育研究·新教师教学(2015年33期)2017-09-27 10:14:53
中学生英语·外语教学与研究(2017年3期)2017-05-19 23:18:46
高中数理化(2016年5期)2016-09-26 06:48:04
中北大学学报(自然科学版)(2016年2期)2016-06-16 03:17:34
中学生数理化·高二版(2016年2期)2016-05-30 07:50:39

