关注三角形“四心”与解几的交汇题

安徽省巢湖市第六中学 (238000) 何显龙

关于三角形中的重心﹑垂心﹑内心﹑外心等问题在解析几何中也经常出现，这类问题体现了平面几何与解析几何的相互交融，由于涉及的知识面广，极富思考性和挑战性，是各类选拔性考试的选题对象.下面精选一些典型例题并予以分类解析，旨在探索解析几何中四心问题的解题方法，希望能给读者朋友有所帮助.

1.重心 即三角形三条中线的交点，重心到顶点距离等于它到对边中点距离的两倍.在解析几何中常用重心坐标公式解题.

例1 在平面直角坐标系xOy中，抛物线y=x2上异于坐标原点O的两不同动点A,B满足AO⊥OB.求△AOB的重心G的轨迹方程.

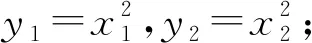
评注：三角形的重心坐标公式是重心性质在解析几何中的重要体现，从而赋予此公式的在具体解题中所起的重要作用.

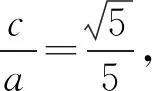
评注：根据重心的性质容易确定弦MN的中点坐标，然后再抓住点在椭圆上运用“点差法”求出弦所在直线的斜率k，这样就解决了问题的核心部分.

2.垂心 即三角形三条高线的交点，在解题中常利用高与边垂直确定直线的斜率关系.

例3 已知圆x2+y2-9x=0与顶点在原点O，焦点在x轴上的抛物线C交于A,B两点，若△AOB的垂心恰为抛物线的焦点，求抛物线C的方程.

评注：由于抛物线方程中只有一个待定参数，所以只要建立一个关于此参数的方程就能解决所求问题，而通过垂心找垂直是很容易得到一个等式的.

评注：由题设中的垂心得到了一个向量的等量关系，它是建立轨迹方程的关键条件.

3.内心 即三角形三条内角平分线的交点，内心到三角形各边的距离相等，解题时常用角平分线的有关性质列式求解.

例5 在△ABC中，A(8，-1)，B(4，2)，内心为M(5，0)，求BC边所在的直线方程.

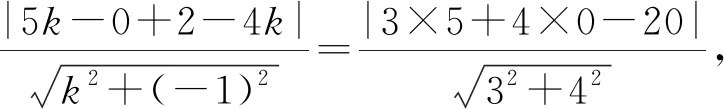
评注：由于已知到内心的坐标，所以可将问题转化为点到直线距离的问题，此处应注意：在设直线方程是需要分斜率存在与不存在的情况讨论，否则易造成失根.

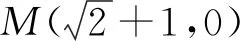
评注：将给出的内心条件转化为点到各边的距离相等，再利用已知的距离挖出了特殊角，很容易就可得到AP、AQ的斜率和直线PQ、AP方程了，下面问题的解决就简单了.

4.外心 即三角形三条边垂直平分线的交点，外心到三角形三个顶点的距离相等.

例7 在△ABC中，A点的坐标是(0，3)，BC边的长为2，且在x轴的区间[-3，3]上滑动，求△ABC的外心M的轨迹方程.

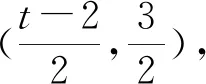
评注：此法是求轨迹方程中的参数法，用参数表示B,C两点坐标后，再求出三角形两边的垂直平分线方程，它们的交点就是外心了，这是从外心的定义角度分析求解的.

例8 设p>0是一常数，过点Q(2p，0)的直线与抛物线y2=2px交于相异两点A,B，设线段AB的中点为H，试证H为△AOB(O为坐标原点)的外心；并求以AB为直径的圆面积最小时直线AB的方程.

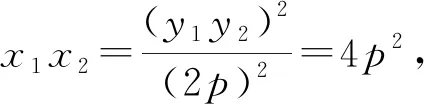
评注：在挖掘出此三角形为直角三角形后，那么三角形的外心就是此三角形斜边的中点，所以找出隐含条件并给予适当的运用就是成功解题的突破口.