RLC串联电路欠阻尼信号衰减常数可视化测量的评估与修正

王子文，李浩源，邓 莉，张诗按，马 彬，国泽镕

(华东师范大学 物理与电子科学学院，上海 200241)

本文利用示波器，采用三种可视化方法测量RLC串联电路欠阻尼信号的衰减常数，通过Desmos软件拟合欠阻尼图像，并对测量结果的准确度进行了评估。采用能量损耗方程式，计算损耗电阻，并对理论值进行了修正，修正后的理论值与实验测量值吻合度提高。

1 原 理

1.1 RLC欠阻尼状态

RLC串联电路如图1所示，电源为方波，当Us从高电平降为0，电路开始放电，这一过程中，电阻、电感、电容的总电压恒为0，列出微分方程为：

图1 RLC串联电路

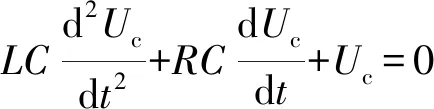
(1)

(2)

1.2 包络线法测量时间常数

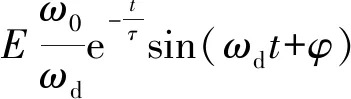
图2 包络线法测量τ值

由图2可以看到，用包络线法测量τ值的确可以反映真实的暂态过程，但只是近似，需要拟合出包络线，增大了操作的难度，引入实验误差。

1.3 图解法测量时间常数

tan(ωdt+φ)=ωdτ

(3)

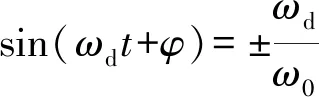
(4)

将(4)带入到公式(2)中，可得：

(5)

其中UCM为振荡峰值。

令UCM为振荡峰值的绝对值，可得：

(6)

取对数可得：

(7)

根据式(7)可以看到最大振幅的对数与时间t呈线性关系，因此，测量一系列(UCM，t)值，做出lnUCM-t直线，根据斜率就可以求出τ值。图解法直接根据曲线上的点进行测量，因此是一种精确的测量方法。

又由式(6)可知，振动的峰值呈指数衰减。如果类似包络线法，作连接振动峰值的点的曲线，测量它从最大振幅降到最大振幅0.368倍处的时间间隔也可以得到τ。包络线法用的是切点不是顶点，自然就有实验误差，只能作为近似求法。

1.4 比值法测量时间常数

根据式(3)可知达到振荡峰值的时间为：

(8)

因此arctan(ωdτ)=kπ+φ，可知达到振荡峰值的时间为：

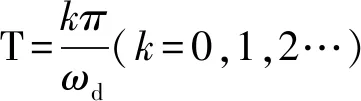
(9)

因此，振荡的周期为：

(10)

根据这一关系，得到一种准确测量τ值的方法，即比值法。

设相隔n个周期的2个最大正峰值为UCM1和UCM(n+1)，将它们相除，根据(6)式可得：

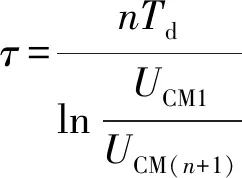
(11)

因此，测量两个最大正峰值和它们之间的振荡周期数也可以算出τ值，比值法也是一种精确测量的方法。

2 实验测量

2.1 包络线法

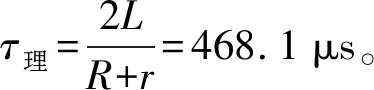
图3 欠阻尼波形图

实验测得电容电压从初始振幅下降到初始振幅0.368倍的时间为ΔT=τ测=400 μs，测量值与理论值的相对误差P=14.5%。

2.2 图解法

保持状态不变进行图解法测量，结果如表1和图4所示：

表1 用图解法测量τ值

由图4可知，lnUCM=-0.002 66t+3.425 14，斜率k=-0.002 66，因此可知τ测=375.9μs，测量值与理论值的相对误差P=19.7%。

2.3 比值法

根据图4，取相隔较远且在直线上的两点，UCM1=29.2V，UCM5=3.6V，n=4，Td=200.0μs，代入公式(11)，可得τ测=382.2μs，测量值与理论值的相对误差P=18.4%。

以上三种方法测得的τ值与理论值之间的相对误差都较大，超过了10%，且测量值都小于理论值，故一定还存在某种因素造成该系统误差。

3 软件拟合

将欠阻尼放电过程电容电压的表达式即式子(2)和相关参数输入到Desmos软件中，得到的图像如图5所示：

图5 软件拟合欠阻尼放电过程

读取图中数据，用图解法处理，结果如表2和图6所示。由图6可知，

lnUCM=-2136.7t+3.376，

斜率k=-2136.7，因此可知τ测=468.0μs，测量值与理论值的相对误差P=0.02%。

表2 软件拟合法数据

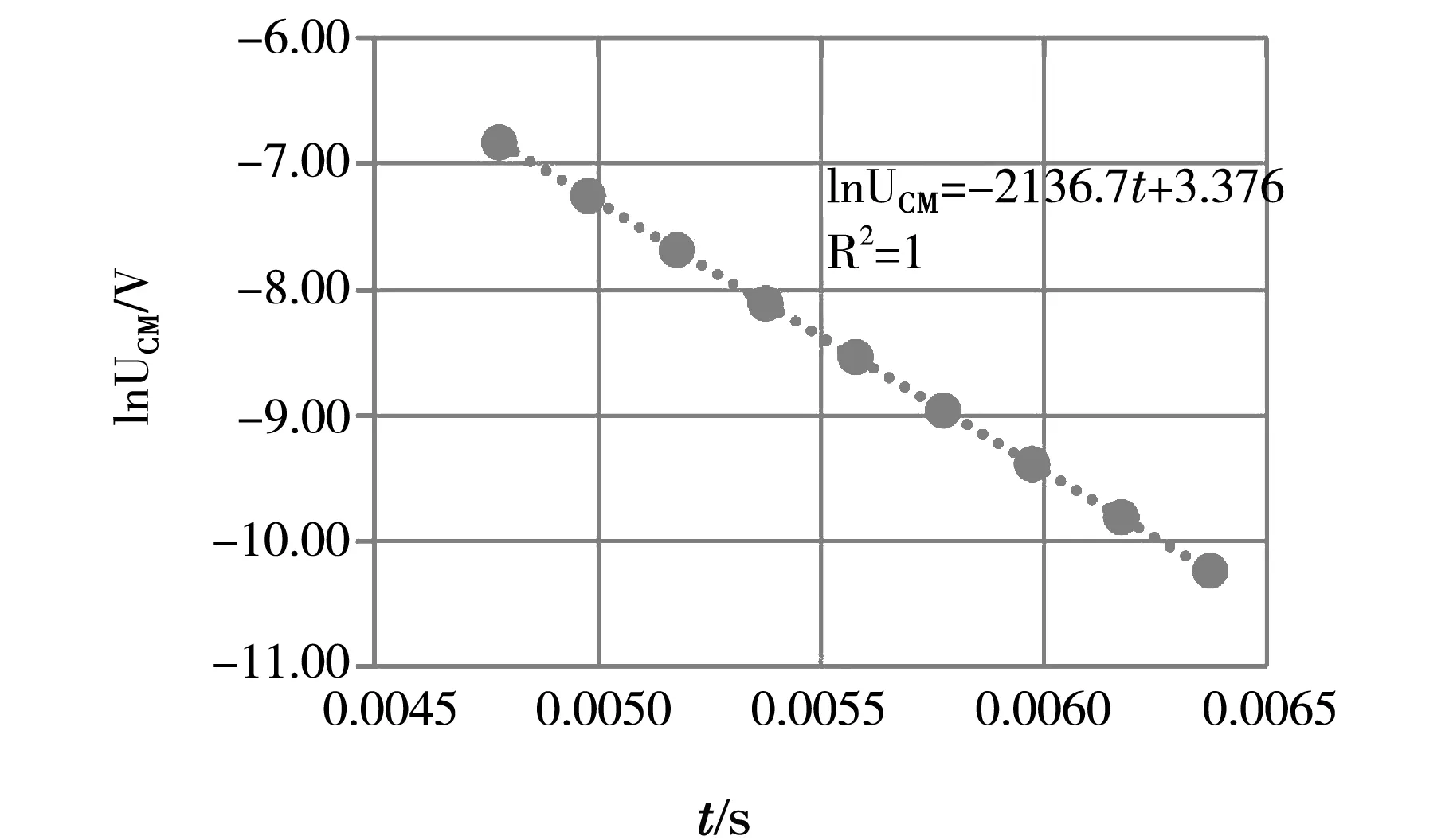
图6 软件拟合法lnUCM-t图

取表2中的第2组和第8组数据，用比值法计算，得到τ测=467.7μs，测量值与理论值的相对误差P=0.09%。

在Desmos软件中只能精确读取曲线上的点的坐标，而使用包络法常常需要精确读取曲线外的点，故测量误差很大，因此包络线法不适用于Desmos软件拟合。

使用图解法和比值法在软件拟合测量时间常数时误差都非常小，小于千分之一，说明这两种方法的确能够精准测量时间常数。

为什么软件拟合时的误差几乎为零而实际实验中误差却超过了10%呢？这是因为软件拟合相当于实验时使用的仪器都是理想的，而实际上仪器中会有各种损耗，这些损耗可以看成损耗电阻，它们使得电路中总电阻偏大，从而导致时间常数减小。

4 修正理论值

4.1 计算损耗电阻

电路损耗主要来源于电感和电容，因此把电路中总的损耗电阻记为RLC。下面用能量损耗方程式计算出损耗电阻RLC并修正τ值。

由(2)式可得电路中的电流为：

(12)

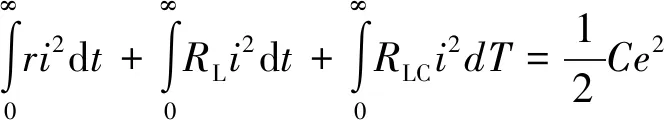
(13)

因此可得：

(14)

将RLC代入，可得：

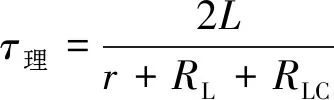
(15)

就可以得到修正后的理论值。

4.2 测量RLC并修正理论值

将各方法测得的时间常数带入式子(14)和式子(15)，就可求出电路的损耗电阻和修正的理论值，如表3所示：

表3 三种方法测得到的RLC与修正的理论值

由表3可知，每种方法的实验测量值与修正理论值符合得都很好，相对误差在1%以内，且图解法和比值法的误差相对于包络法更小，测量更加精确。

5 总 结

采用包络法、图解法、比值法三种可视化方法测量RLC串联电路欠阻尼信号的衰减常数，对三种方法的测量准确性进行了评估，发现包络线法近似测量、还是图解法、比值法精确测量，测得的时间常数都与理论值存在超过10%的较大偏差。说明图解法和比结合Desmos软件拟合欠阻尼图像进行模拟，测得的时间常数，测量值与理论值相差小于0.1%，提高了测量的准确度。采用能量损耗方程式，计算损耗电阻，并对理论值进行进一步修正，理论值与实验测量值相对误差小于1%，说明了该修正方法的有效性。修正后的理论值与精确测量的时间常数符合得很好。本研究也为测量损耗电阻提供了一个新的实验测量方法。