基于SPSS的拉伸法测量金属丝杨氏弹性模量实验数据处理

张 燕

(运城学院 工科实验实训中心，山西 运城 044000)

大学物理实验是高校理工科学生必修的一门理论结合实践的基础课程，学生通过实验操作及对实验数据的分析处理，能更好地为学习物理基础理论提供帮助，提高学生的动手实践能力、实验操作能力及创新能力。本文以大学物理实验中的必选实验之一“拉伸法测量金属丝的杨氏弹性模量实验”为例，与以往文献不同的是一般物理实验教学和科研工作者借助的数据处理软件有EXCEL、ORIGIN等[1]，该研究借助数理统计的实验数据处理方法，利用SPSS软件对测量数据进行二段最小平方法预测分析，建立预测模型，求得金属丝杨氏模量的值。并将采用SPSS软件进行二段最小平方法计算的杨氏模量值与借助EXCEL的逐差法计算的杨氏模量值进行比较，前者更接近公认值。

1 拉伸法测量金属丝的杨氏弹性模量实验

1.1 原理

固体材料在弹性形变范围内，正应力与相应线应变的比值称作杨氏弹性模量，它是度量固体材料受力时形变大小的重要参量。在机械材料、医疗、建筑、通讯等工程设计及材料选用中广泛应用。

设一粗细均匀的金属丝长为L，横截面积为S，当金属丝上端固定，下端悬挂砝码，金属丝在受砝码重力F作用下沿线性方向发生形变，则根据胡克定律，金属丝的应力和产生应变成正比，则：

(1)

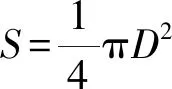
(2)

本实验采用LY-1CCD 型杨氏模量测量仪，如图1所示：

图1 LY-1CCD 型杨氏模量测量仪

1.2 原始数据

用外径千分尺在金属丝的5个不同部位测得其直径，金属丝长度用米尺测量见表1；金属丝下端依次加50克砝码被拉长后再依次减掉砝码用读数显微镜依次读出标尺所处刻度如表2所示：

表1 金属丝长度L和直径D测量 外径千分尺的零点读数：0.008 mm

表2 受力后金属丝伸长量测量

2 金属丝长度和直径数据处理

为了使实验数据更加精确，除了要选取适当的测量仪器外，在测量结果评价和实验数据处理时，往往根据误差的性质来确定误差评价的办法和数据处理的方法。根据误差产生的原因、性质，分为系统误差、偶然误差和粗大误差(过失误差)[2-3]。实践中要对测量数据进行分析检验，准确地区分误差的性质和原因，才能进行有效的数据处理。

2.1 金属丝长度的测量数据分析

金属丝的长度用合成不确定度和相对不确定度表示，根据直接测量量的误差来源计算金属丝长度的不确定度。

金属丝长度的算术平均值

=1.080m

计算5次测量值的标准差，测量值L标准不确定度的A类评价：

标准不确定度的B类评价：

测量值L合成标准不确定度为：

测量值L测量结果表示为：

L=1.080±0.005m

2.2 金属丝直径的测量数据分析

金属丝直径的算术平均值

=0.389mm

计算5次测量值的标准差，测量值D标准不确定度的A类评价：

测量值D标准不确定度的B类评价，外径千分尺的分度值为0.01mm，所以

测量值D测量结果表示为：

D=(0.389±0.006)×10-3mm

3 金属丝杨氏弹性模量的计算

3.1 借助EXCEL的逐差法测算金属丝的弹性杨氏模量

由误差理论知实验中多次测量能减小偶然误差，为了保持多次测量的优越性，通常采用的数据处理方法是逐差法[2-3]。

金属丝杨氏模量的求解公式(2)中F为砝码所受的重力，这里采用逐差法，

ΔM=0.2kg

ΔL=0.107×10-3m

带入Ai数据计算金属丝伸长量。

代入数据计算伸长量的不确定度为：

μ(ΔL)=0

将数据带入公式(2)得

E=1.69×1011N·m-2

由标准不确定度的传递公式估算出杨氏模量的不确定度[2-3]。

μ(E)=0.004×1011N·m-2

金属丝的杨氏模量结果表示为：

E=(1.69±0.004)×1011N·m-2

3.2 采用SPSS软件进行二段最小平方法分析

SPSS软件中二段最小平方法是指两个变量之间存在相互关系时，线性回归只用最小二乘法进行估计[4-5]，输入两组测量数据X、Y通过运算得出相关系数，并根据预测值计算出自变量与因变量之间的模型Y=KX+b。

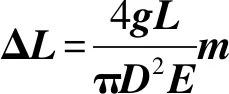
可以看出式中ΔL和m存在线性关系，为斜率K，截距b=0，将表2的数据代入SPSS软件中进行二段最小平方法分析，输出结果如下：

表3 模型拟合度

从表3的输出结果可以看出，复相关系数r=0.993，决定系数R2=0.987，经调整的判定系数AdjustedR2=0.986，判定系数的取值在[0，1]范围内，说明金属丝的伸长量的变化是由金属丝受力的变化引起的，而且预测模型拟合度良好。

表4 方差分析

从表4方差分析结果可以看出，模型的F统计量的观察值为1 041.679，统计检验的相伴性概率Sig趋于0，置信度远远小于0.01，所以回归是高度显著，即金属丝的伸长量因所受力变化的影响显著，可以由金属丝受的不同大小的力来预测金属丝的伸长量，它们所建立的线性关系回归系数存在，且表明预测模型较好，具有统计学意义[5]。

表5 预测模型相关分析

从表5预测模型系数可以看出，预测模型自变量系数为0.449，常数为0.051[4]，由于在输入测量值时单位为毫米，代入公式计算时要换算成国际单位米，可以得到预测模型为Y=0.449×10-3X+0.051×10-3

式中截距b=0.051×10-3结合实验误差，截距趋近于0。

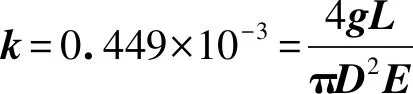
将金属丝直径、长度测量值和不确定度代入上式中计算金属丝的杨氏模量得：

E=(1.98±0.004)×1011N·m-2

4 结 语

从以上逐差法和SPSS软件最小二乘法计算的结果来看，SPSS软件最小二乘法计算的金属丝杨氏模量值更接近于公认值2.0×1011N·m-2。研究结果表明：利用SPSS软件对测量数据进行二段最小平方法分析、检验和处理实验数据使实验数据处理更加简便，并且更加准确的测算出金属丝的杨氏弹性模量。