新四维多卷超混沌Jerk系统的复杂动力学研究*
韩 杰, 杨启贵
(华南理工大学 数学学院, 广州 510640)
0 引 言
20世纪60年代,Lorenz发现一个能够产生蝶形混沌吸引子的三维常微分动力系统,此系统呈现复杂的非线性动力学,引起学术界的广泛研究和深入讨论,由此混沌研究及应用得到蓬勃发展。混沌作为非线性动力学领域的重要分支,相关理论及其应用已渗入到许多其他学科领域。早在1994年,Sprott[1]首次利用计算机穷举法获得一类三维自治Jerk混沌系统,系统形式简单,却具备良好的动力学特性,在物理学界很快就受到了学者们的热烈关注。
近年来,随着非线性动力学的深入发展,人们注意到Jerk混沌系统不仅能够产生多种类型的吸引子,如多重吸引子[2]、隐藏吸引子[3]、共存吸引子[4]等,而且在现实生活中有极好的应用前景,涉及图像加密、网络通信等核心技术。因此,对Jerk系统的研究极为重要。在三维的Jerk混沌研究中,Li等[5]提出具有唯一平衡点的三维Jerk混沌系统,并借助仿真软件加以验证系统的动力学特性;Sang和Huang[6]找到具有两个平衡点的三维二次型Jerk混沌系统并研究其0-Hopf分岔。但实际上,研究人员发现高维或多卷的超混沌系统相较于混沌系统具有更复杂的动力学行为,能更好地适应复杂的实际情景,从而可广泛应用于信息加密等领域。而产生超混沌的系统维数至少是四维,因此对四维超混沌Jerk系统的探讨具有重要价值。目前,探讨Jerk系统如何由三维拓展至四维是很有意义的。在四维的研究中,Vaidyanthan[7]利用3个二次项构造了一类无平衡点的非线性四维超混沌Jerk系统;Dalkiran和Sprott[8]采用指数函数作为非线性项,得到具有一个平衡点的四维Jerk系统,这些研究丰富了四维Jerk系统的类型。最近,关于四维非光滑Jerk系统的研究也有一些成果。如Hosham[9]提出具有4个平衡点的分片四维Jerk系统,并分析系统复杂的分岔现象。此外也有学者通过引入控制忆阻器来构造能产生多卷吸引子的系统,基于此方法,Wang等[10]得到了具有8个平衡点的四维超混沌多卷Jerk系统;Xia等[2]获得具有21个平衡点且能产生多卷的超混沌Jerk系统;随后Zhang和Wang[11]构造出具有无穷多个平衡点的超混沌四维多卷Jerk系统,他们构造的多卷吸引子相比单卷和双卷的吸引子展现出了更为复杂的结构。迄今为止,还没有一个普适方法可用来构造多卷系统,如何找到一个能产生多卷的非线性系统是个难点。研究发现能产生多卷的超混沌Jerk系统往往具有多个平衡点且不光滑,那么仅有一个平衡点的光滑Jerk超混沌系统能否产生多卷吸引子是个值得探讨且有意思的问题,但目前关于这方面的综合研究还比较少,因此对这类系统的研究极具意义和价值。
针对上述问题,提出了具有唯一平衡点的新四维多卷光滑超混沌Jerk系统,系统仅含有一个非线性项。首先,给出系统的具体形式,通过分析系统的对称性及耗散性、Lyapunov指数和吸引子相图来讨论系统的基本性质。然后从系统局部特征角度出发,分析系统蕴含的复杂动力学行为,包括对平衡点和Hopf分岔的相关分析,严格证明了两者的存在性。最后通过数值模拟有效刻画了系统的Lyapunov指数谱、分岔图、相图以及Poincaré映射,展示了新系统的复杂动力学特征。
1 新四维多卷超混沌Jerk系统
2000年Sprott[12]提出了一个三维Jerk混沌系统:
(1)

基于系统式(1),利用反正切函数来逼近符号函数,结合多卷混沌系统的设计方法[13],设计反馈控制器,引入线性反馈控制项-au及非线性控制项F(x),可获得如下新四维连续多卷超混沌Jerk系统:
(2)


(3)

(a) N=M=1

(b) N=1, M=2
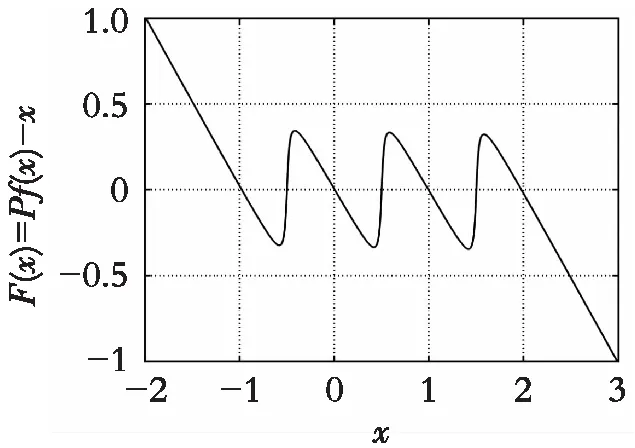
(c) N=2, M=1
固定系统式(2)的参数,对其进行坐标变换:
(x,y,z,u)→(-x,-y,-z,-u)
系统的形式保持不变,因而系统式(2)关于原点(0,0,0,0)对称。
系统式(2)的散度为
当b>0,即▽V<0时,系统式(2)是耗散的。这意味着系统式(2)在无穷远处会以指数速率-b收敛到0。
当系统式(2)的参数(a,b,k1,k2,Q,N,M)=(0.01,0.63,0.01,1,9 999,1,1)时,利用Matlab数值模拟,计算得到系统式(2)的Lyapunov指数:
LE1=0.106 9,LE2=0.107 4LE3=0.000 0,LE4=-0.844 4
由此可知系统式(2)在该参数条件下是超混沌的。根据混沌系统Lyapunov维数的定义,计算得出系统式(2)的Lyapunov维数DL≈3.253 7,此时系统式(2)对应的相图如图2所示,可以看出系统产生了3卷超混沌吸引子。
其次固定系统式(2)的参数(a,b,k1,k2,Q)=(0.01,0.68,0.01,1,9 999),同理可得到相对应的Lyapunov指数:
LE1=0.090 9,LE2=0.091 2LE3=0.000 0,LE4=-0.862 2
以及Lyapunov维数DL≈3.211 2。通过调节函数f(x)中的控制参数N和M,发现系统式(2)可以产生具有不同卷数的超混沌吸引子,其对应二维平面的相图如图3所示。

(a) x-y-z空间

(b) x-y-u空间

(c) x-z-u空间

(d) y-z-u空间

(a) N=M=2

(b) N=4, M=2

(c) N=3, M=5
2 局部动力学分析
2.1 平衡点存在性和稳定性
系统的局部动力学特征可通过平衡点的性质反映出来,现主要研究的是系统式(2)平衡点的存在性及稳定性,探究平衡点处于不同状态时的参数范围。
系统式(2)的平衡点可由方程组式(4)确定:
(4)
λ1=-0.000 1,λ2=-0.844 7λ3,4=0.107 4±1.086 2i
此时系统式(2)在平衡点E处的流形具有两个稳定方向和两个不稳定方向,因此平衡点E是一个鞍-焦点。
定理1 设
Ω= { (a,b,k1,k2)|ak1> 0,b>ak1+ 1,(b-ak1-1)(abk2+ak1+ 1) >ab3k1}
则系统式(2)的平衡点E满足如下结论:
当系统式(2)的参数(a,b,k1,k2)∈Ω时,其平衡点E是渐进稳定的;当系统式(2)的参数(a,b,k1,k2)∉Ω时,其双曲平衡点E是不稳定的。
证明系统式(2)在平衡点E附近的Jacobi矩阵为

λ4+bλ3+(ak2+1)λ2+(abk2+ak1+1)λ+abk1=0
(5)
计算如下行列式:


于是当系统式(2)的参数(a,b,k1,k2)∈Ω时,有Δ1>0,Δ2>0,Δ3>0,Δ4>0,根据Routh-Hurwitz判别准则可得,系统式(2)的平衡点E是渐进稳定的;当参数(a,b,k1,k2)∉Ω,系统式(2)的双曲平衡点E是不稳定的。
2.2 Hopf分岔存在性
Hopf分岔是混沌动力学中一种重要的分岔类型,现研究系统式(2)在平衡点E(0,0,0,0)附近的Hopf分岔。


则当系统式(2)的参数b经过其临界值bj时,系统会发生Hopf分岔,其中
证明假设系统式(2)的特征方程式(5)存在一对纯虚根λ=±iω(ω∈R+),将纯虚根iω代入特征方程式(5)可得:
ω4-(ak2+1)ω2+abk1+iω(abk2+ak1+1-bω2)=0
(6)
由式(6)推出方程组:

通过求解方程组有:

利用盛金公式[14]可解得,当Δ=0时,有:


由此可解得:

再根据特征方程式(5)可得:

那么有:
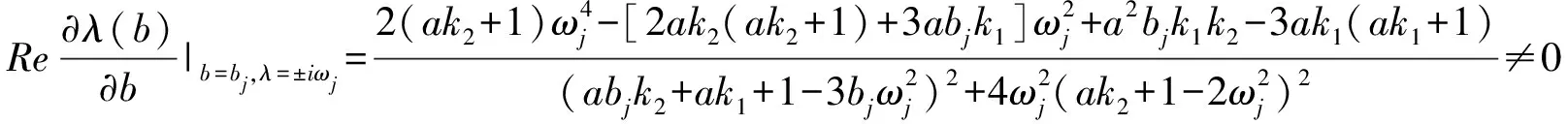
因此,系统式(2)满足中心流形定理中Hopf分岔存在的第二条件[15]。由Hopf分岔存在性定理得证,当系统式(2)的参数b越过其临界值bj时,系统发生了Hopf分岔。
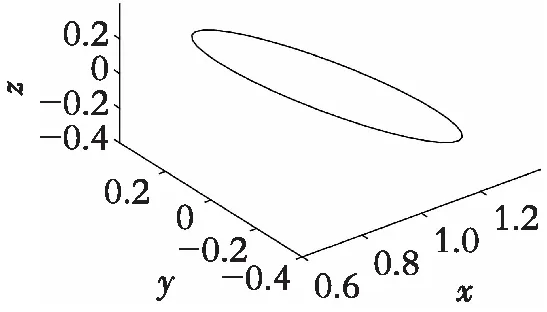
为了验证定理2的合理性,利用数学软件对系统式(2)进行数值仿真验证,选取系统式(2)的参数(a,k1,k2)=(0.01,0.01,1),通过计算可得b1=1.00,b2,3=161.08。现验证b1=1.00的情形,选取函数f(x)的参数Q=9 999,N=M=1,当系统式(2)的参数b=0.99 λ1=-0.000 1,λ2=-0.995 0λ3,4=0.002 5±1.007 5i 此时系统式(2)在平衡点E处具有两个稳定流形和两个不稳定流形,平衡点E是一个鞍-焦点,系统式(2)的吸引子相图如图4(a)所示,此时系统生成了一个多卷吸引子;当系统式(2)的参数b=1.01>b1时,平衡点E对应的4个特征值如下所示: λ1=-0.000 1,λ2=-1.005 1λ3,4=-0.002 4±1.002 5i 特征值所有实部为均为负数,此时系统式(2)的平衡点E是稳定的,图4(b)展示了系统的吸引子相图,由此看出系统存在周期轨。因此,系统式(2)的参数b穿过b=1.00时,平衡点的状态由不稳定变为稳定,系统发生了Hopf分岔,因此验证了定理2的结论。 (a) b = 0.99 (b) b = 1.01 固定系统式(2)的参数(a,k1,k2,Q,N,M)=(0.01,0.01,1,9 999,3,2),选定参数b在区间[0.6,1.1]变化时,系统的Lyapunov指数谱和分岔相图如图5所示。 (a) Lyapunov指数谱 (b) 分岔相图 结合图5(a)-5(b)可以看出:随着参数b的增加,系统式(2)的动力学状态经历了从超混沌到拟周期的过程。特别地,当参数b选取特定值时,系统式(2)对应的4个Lyapunov指数如表1所示,对应的吸引子相图如图6所示。从表1可以看出:系统式(2)的动力学经历了从超混沌到混沌、拟周期到周期这4个状态的变化,从图6可以看出系统式(2)具有复杂的动力学特征。 (a) b = 0.850 (b) b = 0.999 (c) b = 1.000 (d) b = 1.003 表1 系统式(2)在参数 (a, k1, k2, Q, N, M)=(0.01, 0.01, 1, 9 999, 3, 2) 时的Lyapunov指数 选取系统式(2)的参数(a,b,k1,k2,Q,N,M)=(0.01,0.63,0.01,1,9 999,1,1)时,系统的吸引子在二维平面的Poincaré映射如图7所示,表明系统式(2)存在超混沌吸引子。 (a) x-y平面 (b) x-z平面 (c) x-u平面 (d) y-z平面 立足于Jerk混沌系统的吸引子及平衡点两个视角,通过反馈控制器技术,建立四维多卷超混沌光滑Jerk系统。详细分析了所得系统的基本性质,包括平衡点的存在性及处于稳定状态时的参数条件、Hopf分岔存在性等,发现系统是耗散的且关于原点对称,系统仅有一个平衡点,为鞍-焦点类型,且存在Hopf分岔现象。进一步利用数学软件Matlab进行数值仿真得到系统的Lyapunov指数谱、吸引子相图和Poincaré映射等特征,验证了提出的新系统具有周期、混沌、拟周期、超混沌吸引子的复杂动力学现象。研究不仅丰富了多卷Jerk系统的类型,而且对进一步深入理解四维多卷超混沌光滑Jerk系统的动力学具有重要的理论意义及实际价值。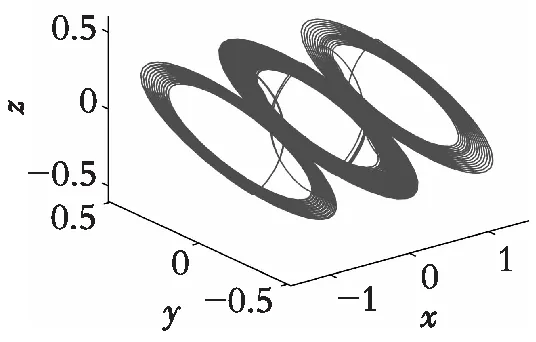

3 复杂动力学分析










4 总 结

