Distributed event-triggered adaptive control for second-order nonlinear uncertain multi-agent systems
Ming XIAO, Zhitao LIU, Hongye SU
The State Key Laboratory of Industrial Control Technology, Institute of Cyber-Systems and Control, Zhejiang University,Hangzhou 310027, China
KEYWORDS Adaptive distributed control structure;Event-triggered control;Multi-agent systems;Second-order nonlinear models
Abstract In this paper, the event-triggered consensus control problem for nonlinear uncertain multi-agent systems subject to unknown parameters and external disturbances is considered. The dynamics of subsystems are second-order with similar structures, and the nodes are connected by undirected graphs. The event-triggered mechanisms are not only utilized in the transmission of information from the controllers to the actuators, and from the sensors to the controllers within each agent, but also in the communication between agents. Based on the adaptive backstepping method,extra estimators are introduced to handle the unknown parameters,and the measurement errors that occur during the event-triggered communication are well handled by designing compensating terms for the control signals.The presented distributed event-triggered adaptive control laws can guarantee the boundness of the consensus tracking errors and the Zeno behavior is avoided.Meanwhile, the update frequency of the controllers and the load of communication burden are vastly reduced. The obtained control protocol is further applied to a multi-input multi-output second-order nonlinear multi-agent system, and the simulation results show the effectiveness and advantages of our proposed method.
1. Introduction
Cooperation in Multi-Agent Systems (MASs) has attracted significant interest in both science and engineering due to a number of applications, including robots, smart grids, and aeronautics.1,2Distributed consensus control means that the information of each agent’s neighboring area is collected to generate the local control signal, so comes the problem that only part of the agents can fully access the exact desired trajectory. Moreover, the dynamics of agents are almost all nonlinear with the external disturbances and intrinsic uncertainties which makes the distributed consensus control problem for nonlinear MASs more complicated.For the consensus control problem of nonlinear MASs, a connectivity algorithm is proposed for second-order dynamics by introducing local adaptation strategies in Ref.3. The case with unknown nonlinear dynamics, immeasurable states, and disturbances is investigated by fuzzy logic systems and high-gain observers in Ref.4, and synchronization is realized for Lipschitz-type nonlinear systems with positive-definite inner coupling matrix over the directed switching topology in Ref.5. In Ref.6, new compensating terms are introduced to counteract the effects caused by the uncertainties,and asymptotically consensus tracking for MASs with non-identical dynamics is achieved. In Ref.7, the assumption of the linear expressible reference trajectory in Ref.6is relaxed, and extra estimates are introduced to design a distributed adaptive controller.
Note that, due to the complexity of the system dynamics,many communication and computation resources are consumed in the methods to tackle the nonlinear functions and uncertainties. Therefore, how to reduce the communication burden for MASs is a critical concern since the communication and energy resources are limited in practice.Due to its characteristic that the transmitted signals are updated only when the designed triggered conditions are satisfied, the event-triggered control approaches have established fruitful results in the consensus tracking problems for nonlinear MASs.8–15In Ref.8,the consensus problem of MASs modeled as double integrators is solved by a distributed event-triggered sampling control scheme, and the results are further extended to the nonlinear dynamics. Ref.9is concerned with the event-triggered leaderfollowing consensus problem of second-order MASs with nonlinear dynamics under the directed topology. Robust consensus for nonlinear second-order MASs with uncertainties is investigated by an event-triggered distributed control protocol in Ref.10. In Ref.11, three inspiring event-triggered strategies are designed for uncertain nonlinear systems with unknown system parameters, which relax the ISS assumption. In Ref.12,cooperating with the disturbance observer and adaptive method,a distributed event-triggered controller is designed for nonlinear MASs with unknown disturbances.
Despite the triggered communication between the controllers and actuators, the event-triggered mechanism also plays an interesting role during the information transmission between agents,which is called as event-triggered broadcasting mechanism.The states’information is collected by the individual agent and then broadcasted to its neighboring agents. In Ref.13, the event-based broadcasting strategy is proposed for multi-agent coordination.In Ref.14,the event-based consensus problem for linear MASs with external disturbances is addressed without continuous communication. An eventbased control algorithm is first proposed for synchronization problem of networks of generic linear systems over directed communication topologies.15In Refs.13–15, each agent decides itself when its current state is transmitted to the neighbors, so the communication burden can be vastly reduced. It’s worth mentioning that the results above are based on MASs with linear dynamics, the triggered communication mechanisms between agents for nonlinear uncertain systems are still under investigation. In Ref.16, distributed adaptive consensus tracking control schemes are developed for uncertain nonlinear first-order systems with event-triggered communication. In Ref.17,the adaptive fuzzy event-triggered containment control problem is addressed for uncertain nonlinear strict-feedback MASs.
Second-order Multi-Input Multi-Output (MIMO) dynamics is vital for representing the system model of the quadrotors18–20and other vehicles21–24like small UAVs.23,24So it is of great interest to investigate the consensus tracking control strategy for the second-order MIMO MASs,and there are lots of results about this issue and its huge potential applications.The consensus strategies for multi-vehicle systems modeled as double-integrator dynamics are solved in Ref.21,and formation tracking analyses are studied in Ref.18with the application to quadrotor formation flying.An adaptive finite-time control algorithm is developed for second-order multivariable systems to achieve the attitude tracking of quadrotor UAVs in Ref.19.For nonlinear second-order MIMO systems in strict feedback form, the model uncertainties and external disturbances are fully compensated for small UAV,22,23and the formation tracking performance is enhanced in Ref.25. Because of the limited energy, it’s vital to investigate the event-triggered consensus control for MIMO nonlinear MASs.Ref.26is concerned with distributed containment maneuvering of second-order uncertain MIMO MASs with event-triggered communication and actuation.
Motivated by the aforementioned results, the distributed event-triggered consensus tracking problem for second-order nonlinear MASs with unknown parameters and external disturbances is investigated.We aim to achieve exponentially consensus tracking and meanwhile save the communication and computation resources, so event-triggered mechanisms are adopted to reduce the update frequency of the controllers and the load of communication burden inside each agent and between agents. Adaptive estimators are introduced to handle the uncertainties, and the compensating terms are designed in the control signals and the adaptive update laws to tackle the measurement errors that occur during the triggered communication. The main contributions of our approach can be summarized as follows:
(1) The system model is general with second-order dynamics, unknown parameters and external disturbances,and our approaches to handle the uncertainties need less communication and energy resources compared with Ref.7.Besides,the compensating terms in the controllers and adaptive laws are designed to enhance the tracking performance. Moreover, the control protocols for second-order single-input single-output systems are extended to the multi-input multi-output case while good tracking performance can still be achieved with a few communication resources.
(2) With event-triggered control schemes, the update frequency for control signals is reduced and computation resources are saved. Furthermore, the event-based broadcasting strategy is first utilized in the control protocol to achieve the consensus tracking for second-order nonlinear MASs, which can vastly reduce the load of communication burden between and inside agents. The triggered conditions are designed as fixed-threshold for the states signal and the controller signals,and the measurement errors are well compensated. Meanwhile, the Zeno behavior is avoided.
The remainder of this paper is organized as follows.We formulate the distributed consensus problem of second-order nonlinear MASs in Section 2. The event-triggered adaptive controllers are shown in Section 3. In Section 4, the stability of the closed-loop system is analyzed. Simulation results and the extended control strategy are given in Section 5 and Section 6, respectively. Finally, we conclude this paper in Section 7.
Notation: Throughout this paper, N means the number of agents; ‖∙‖ denotes the Euclidean norm; λmax(A ) means the maximum eigenvalue of matrix A,and λmin(A )means the minimum;for an unknown vector Δ, ^Δ is the estimate of Δ,and the estimation error Δ~is defined as Δ~=Δ- ^Δ.
2. Problem formatting
2.1. System model
We consider a group of N agents, and the dynamic characteristic of agent i is second-order with the unknown parameters and external disturbances, which can be presented as
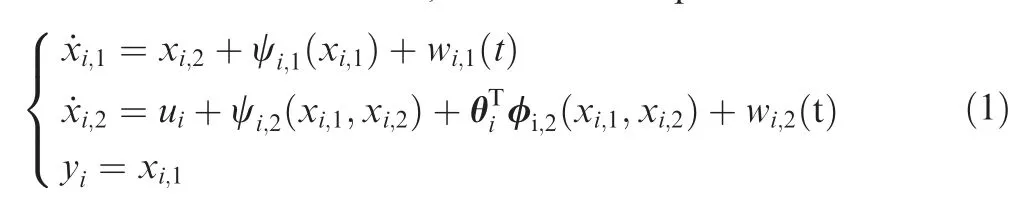
where xi;1;xi;2∊R are the state of agent i;θi∊Rpiis a vector of unknown constants; φi;j:Rj→Rpiis a vector of known smooth nonlinear functions and ψi;j:Rj→R is a known smooth nonlinear function for i=1;2;...;N; wi;1∊R and wi;2∊R denote uncertain external disturbances. Inspired by Ref.6, the desired trajectory for all the agents yrcan be expressed as

where fr=[fr;1;fr;2;...;fr;k]T∊Rkis a vector of functions which is known to all the subsystems, and πr=[πr;1;πr;2;...;πr;k]T∊Rkis a constant vector which is available only to the subsystem with μi=1. In this paper,the 2th derivative of the desired trajectory yr(t) is set as bounded and piecewise continuous.
2.2. Information transmission graph
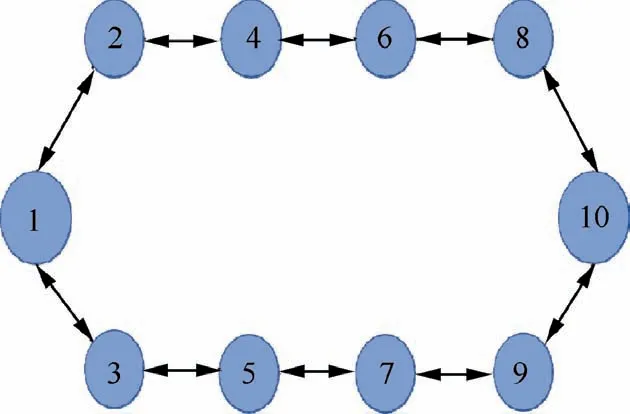
Suppose the communication topology between agents can be represented by an undirected graph G≜(V;E),where V denotes the node set and ε ⊆V×V means the set of edges between two agents. If an edge (i;j)∊E, it means that agent i can get the information from agent j,and then agent i is called a neighbor of agent j.Since the graph is undirected,agent j is also a neighbor of agent i. We denote the set of neighbors as Ni≜j ∊V :(i;j)∊E for agent i. The connectivity matrix is defined as A=[ai;j]∊Rn×n, where ai;j=1 if (i;j)∊E and ai;j=0 otherwise. We introduce the in-degree matrix Δ such that Δ=diag(Δi)∊Rn×nwith Δi=Σj∊Niai;j, which means the ith row sum of A. The Laplacian matrix of the graph is defined as L=Δ-A. If the ith agent can access the desired reference yi, μiis set as μi=1; otherwise μi=0. We assume the undirected communication graph G to be fixed and connected, and then the matrix (L+B) is symmetric positive defined with B=diag{μi}.
Different from the time-triggered scheme, the value of the controllers designed by event-triggered mechanism is updated only when specific conditions are satisfied, which reduces the frequency of the controllers’ update and the load of information transmission burden between controllers and actuators.In addition, the event-triggered mechanisms are also utilized in the information transformation of part of the state signals between agents and inside agents.
For agent i, the specific flow of information can be described as: The sensor of agent i can get the exact information of states xi;1;xi;2, and then the exact information of xi;1is transmitted to the controller and the neighbouring agents of agent i by continuous communication. The transmission of xi;2is based on the designed event-triggered broadcasting mechanism, so both the neighborhood and the controller of agent i can only access the triggered state information x-i;2.What’ more, the value of control signals received by the actuator is updated only when specific triggered conditions are satisfied. In a whole, the event-triggered communication exists from the sensors to the controllers,the controllers to the actuators, and agents to their neighborhoods, so the load of communication burden is reduced vastly and the energy resources are saved. The structure of our control scheme is shown in Fig. 1.
2.3. Design of event-triggered broadcasting mechanisms

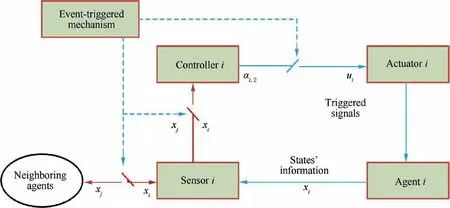
Fig. 1 Structure of our designed event-triggered control protocol.

3. Design of distributed event-triggered adaptive controllers



Remark 1. Since the derivative information of the first state channel is required for Step 2 to stabilize the error variable system, the measurement errors that occured during the eventtriggered communication of xi;1and xj;1will make the controller design procedure consume more computation resources, affect the tracking performance, and even disrupt the system stability.There has to be a trade-off between the event-triggered mechanisms and the whole closed-loop system performance.Thus the transmission of xi;1for agent i is set as continuous communication.
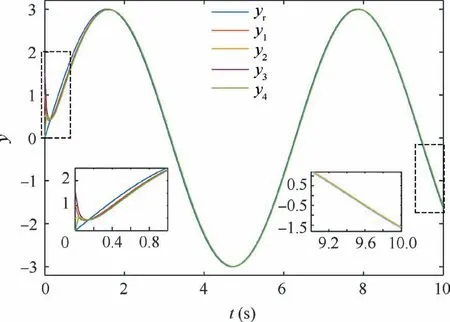
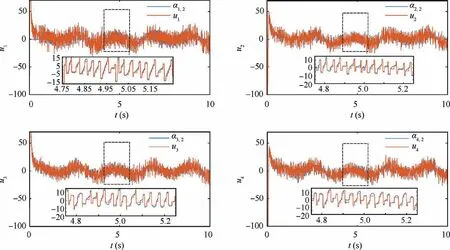
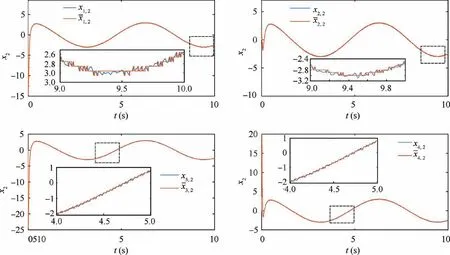
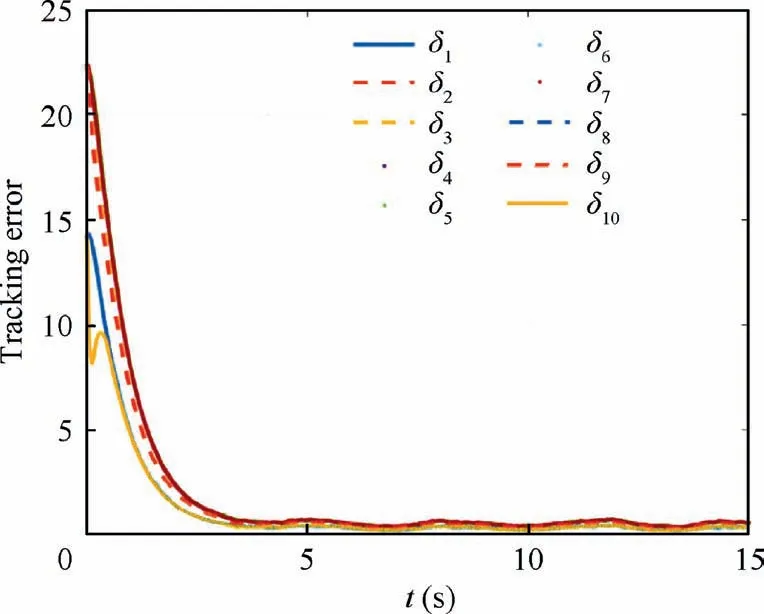
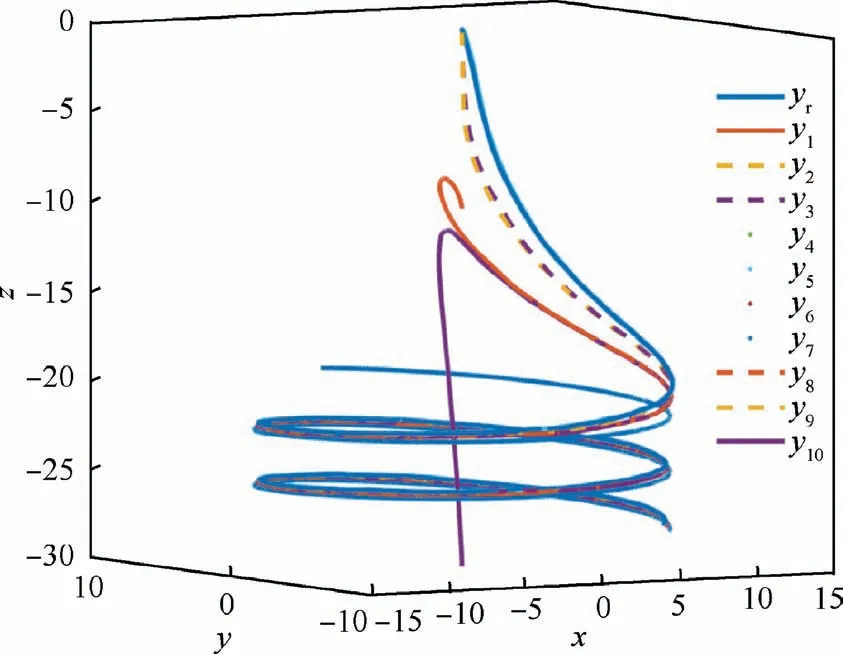
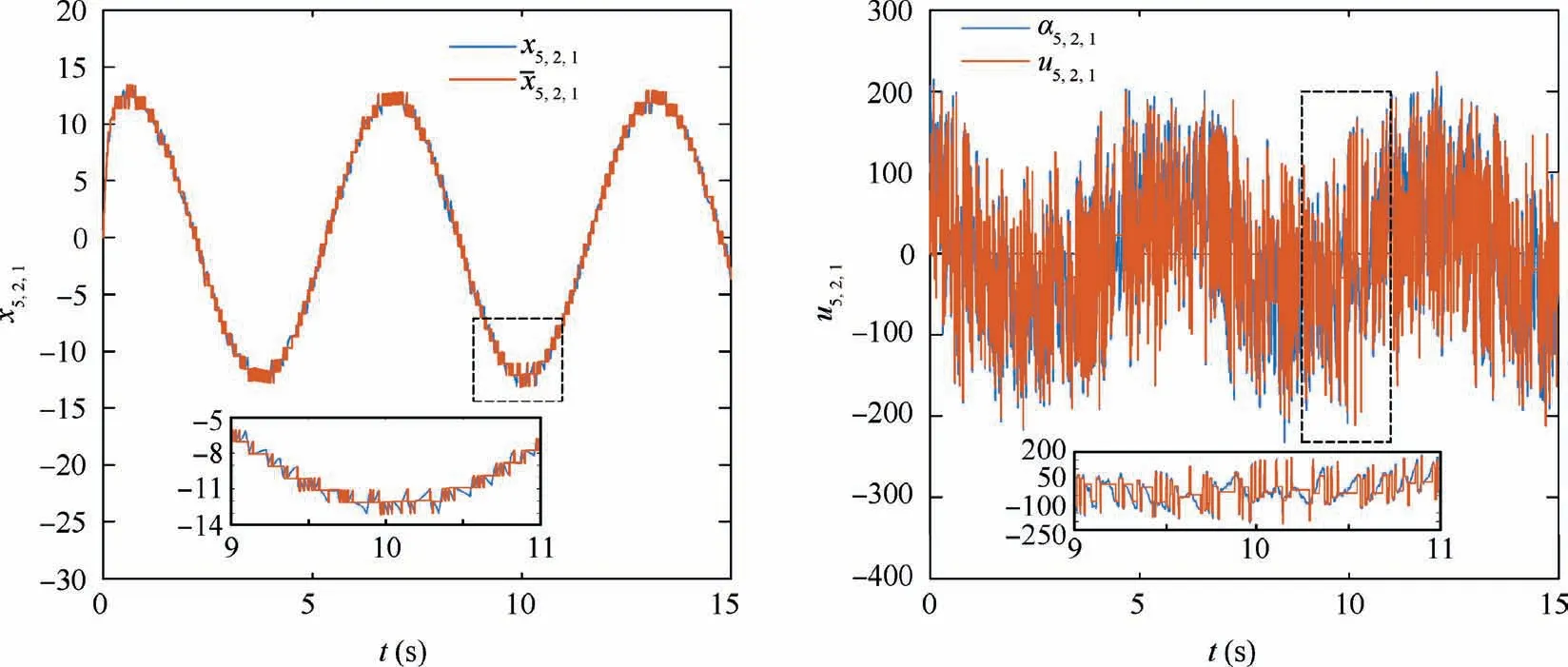
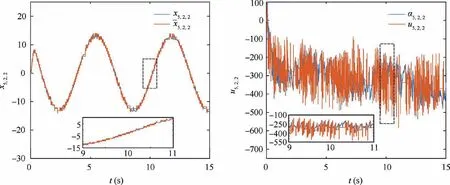
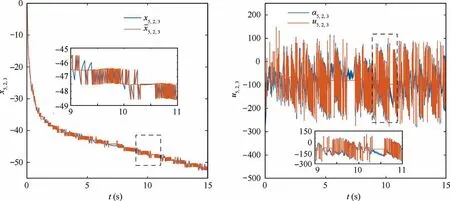
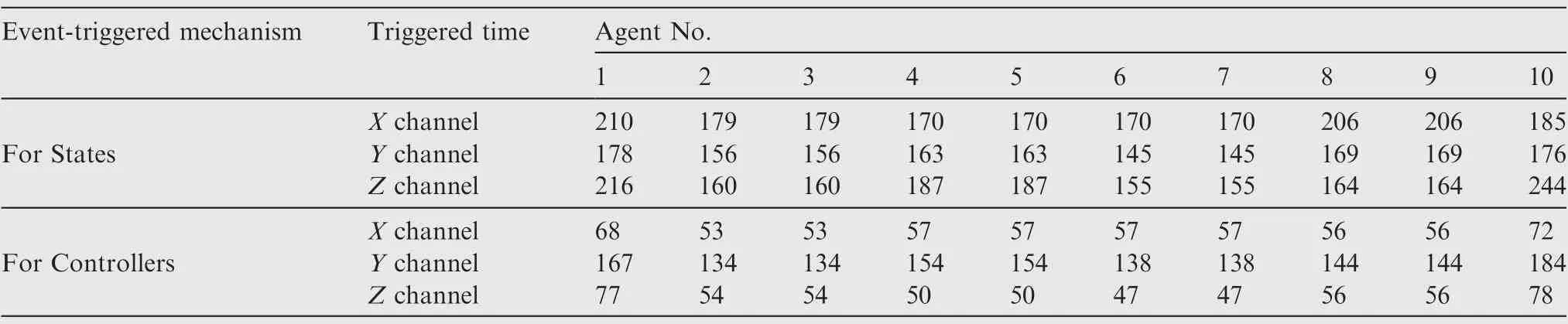
Remark 2. According to the triggered mechanisms designed for the state signals in Eq.(3),when βi(t ) Remark 3. The triggered control signal designed in Eq.(18) can also save the communication and energy resources following the analysis in Remark 2. To tackle the measurement errors, compensating terms are designed in the control signals. In addition,the σ-modification term is adopted in the adaptive estimators,for which specific conditions should be satisfied to ensure the stability of the closed-loop system. We establish our main theorem as follows: Theorem 1. Considering a group of N nonlinear multi-agent systems under external disturbances modeled as Eq.(1)with the distributed controllers in Eq.(16),the triggered conditions in Eq.(3)and Eq.(18),and the adaptive update laws in Eq.(11)and Eq.(20), the closed-loop system is globally stable and it can be realized that all the signals are bounded and the tracking errors arrive at a set adjusted by designed parameters exponentially.Besides, the Zeno behavior is excluded for all the agents. Proof. The Lyapunov function is designed as follows to ensure the boundness of closed-loop signals, and it is obvious that the Lyapunov function is positive defined. In this part,we choose a second-order SISO multi-robotic system to illustrate the effectiveness of our proposed control strategy. As described in Ref.17, each robotic with external disturbances and unknown parameters is modeled as where θi;1=-10,wi;1=0.01 sin(2πt),and wi;2=0.1 sin(πt)for i=1;2;3;4. The desired trajectory is selected as yr=3 sin(t).The control objective is to design event-triggered adaptive controllers so that xi;1can asymptotically track the desired reference signal yrin all the subsystems.The multi-agent system contains four agents and only agent 1 can access the desired trajectory.The communication graph can be described as: agent 1 is a neighbor of agent 2 and 3;agent 2 is a neighbor of agent 1 and 4;agent 3 is a neighbor of agent 1 and 4;agent 4 is a neighbor of agent 2 and 3. The initial states are set as zero except that xi;1(0 )=1, xi;20( )=0.5, xi;3(0 )=1.5. the control parameters are chosen as mi=0.1, m-i=4, ci;1=ci;2=45, li;1=li;2=5,Γi=Γri=1,θi1;0=-9,πri;0=3,Fi;0=0,ηi=e-0.01t. Fig. 2 Trajectory of xi;1 for four agents. The tracking performance of all the agents’ output compared to the desired trajectory is shown in Fig.2 which denotes that good tracking performance is obtained. Note that in Fig. 2 the tracking error still exists due to the positive bound constant χ in Eq.(24).Fig.3 shows the virtual continuous signal and the triggered control signal for four agents,and Fig.4 represents the real state signal and the triggered one. Figs. 3 and 4 well indicate the effectiveness of our designed fixedthreshold strategies. The triggered times are 199, 112, 233,and 203 for states’ broadcasting in four agents, and 482, 345,580, 575 for control signals in four agents, respectively. The triggering events during the states broadcasting and the control signals are shown in Fig.5,and the amount of triggering times are far less than the communication times under continuous control protocol.The simulation results with four agents are quite convincing, it can be seen that asymptotically exponentially consensus tracking is achieved, and the communication resources are saved compared with the continuous scheme. In this section, we shall apply our proposed distributed consensus control protocol to solve the control problem for a second-order MIMO system with unknown parameters and external disturbances, and necessary improvements are made to extend the results for SISO to the dynamic level at MIMO.The system model dynamic is chosen as where xi;1∊R3contains three channels as a position vector in(x;y;z)coordinates,and xi;2∊R3means the velocity vector of xi;1. ui;yi;wi;1;wi;2∊R3denotes the system input, output and external disturbances, ψi;1;ψi;2;φi;2are known vectors of nonlinear functions, and θiis the vector of unknown parameters.The functions are expressed as Fig. 3 Virtual law ai;2 and triggered signal ui. Fig. 4 State signal xi;2 and triggered signal x-i;2. Different form Ref.26, the external disturbances are more general than white noises, and the nonlinear functions are decomposed into known functions and unknown parameters.The control objective is to design event-triggered adaptive controllers so that the three channels of xi;1can asymptotically track the desired reference signal,with the triggered communication existing from sensors to controllers,controllers to actuators, and agents to their neighborhoods. The consensus tracking errors and the coordinates which are changed for backstepping method are defined as Fig. 6 Communication topology between subsystems. Fig. 7 Norm of tracking errors. By following the analysis above, the closed-loop system is globally stable in the sense that all the signals are bounded and the exponentially asymptotically tracking is achieved,and the Zeno behavior is avoided. Fig. 8 Trajectory of each subsystem. For the simulation, the desired trajectory is selected as xr=10 sin(t), yr=10 cos(t), zr=-0.5t-20. The initial states are set zero except that z1;1;3(0 )=-10,z10;1;3(0 )=-30, the control coefficients are chosen as ci;1;k=10, li;2;k=1, ci;2;k=9, πi;10=10, πi;20=10, πi;30=0.5,Γi=5, Γri=1, rπi;k= rθik= 10, θi;10=34, θi;20=-25,θi;30=-7. The event-triggered parameters are chosen as mi;1=100, m-i=1. Fig. 9 Triggered state and control signal for X channel in agent 5. Fig. 10 Triggered state and control signal for Y channel in agent 5. Fig. 11 Triggered state and control signal for Z channel in agent 5. Table 1 Triggering times of multi-agent systems (total sampling time is 15001). In this paper,the event-triggered consensus control for secondorder nonlinear uncertain multi-agent systems with unknown parameters and external disturbances is investigated. On the basis of adaptive backstepping method, extra estimators are introduced to handle the uncertainties and compensating terms are designed to tackle the measurement errors that occured during the event-based information transmission. With eventtriggered control scheme, the communication burden both inside agents and between agents is reduced remarkably meanwhile the satisfactory performance is maintained. Moreover,the system model dynamic is extended from the single-input single-output to multi-input multi-output MASs under specific changes in the control strategy.Future research direction may include adaptive control protocols for agents connected by more general graphs under event-triggered communication. Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgements This work was supported by National Key R &D Program of China (No. 2018YFA0703800) and Science Fund for Creative Research Group of the National Natural Science Foundation of China (No. 61621002).4. Stability analysis

5. Simulation results
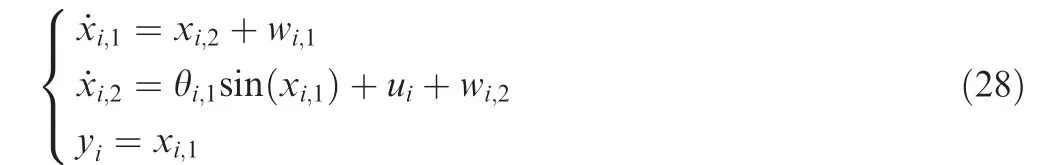
6. Application to a nonlinear MIMO multi-agent system

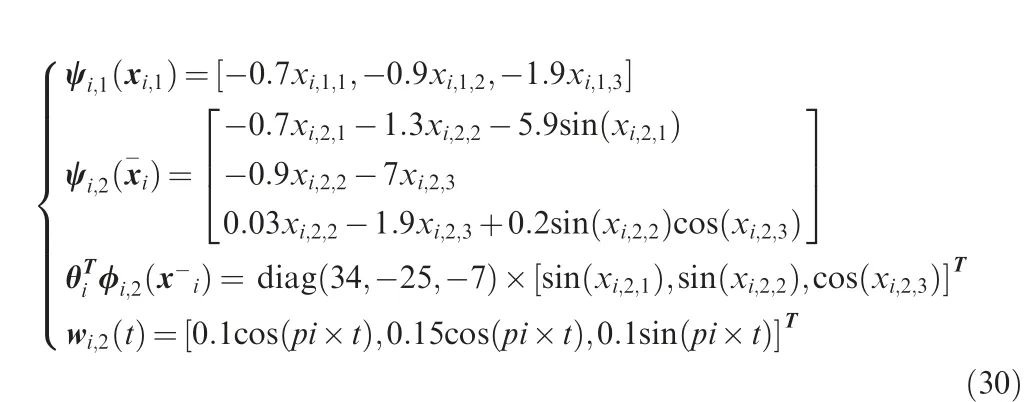
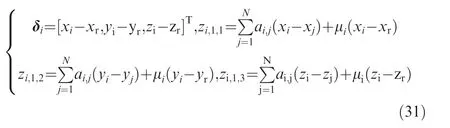



7. Conclusions
 CHINESE JOURNAL OF AERONAUTICS2021年10期
CHINESE JOURNAL OF AERONAUTICS2021年10期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Direct dynamic-simulation approach to trajectory optimization
- A strong robustness open-circuit fault diagnosis strategy for novel fault-tolerant electric drive system based on d-q-axis current signal
- Nonlinear vibration response characteristics of a dual-rotor-bearing system with squeeze film damper
- Ground maneuver for front-wheel drive aircraft via deep reinforcement learning
- Numerical simulation of a UAV impacting engine fan blades
- Recent advances in precision measurement &pointing control of spacecraft
