Direct dynamic-simulation approach to trajectory optimization

Sung Wook HUR, Seong Han LEE, Yong Hyeon NAM, Chang-Joo KIM

Department of Aerospace Information Engineering, Konkuk University, Seoul 05029, Republic of Korea

KEYWORDS Trajectory optimization;Direct method;Hermite spline interpolation;Pseudo-spectral integrator;Soft lunar landing

Abstract This paper proposes a new direct method for an efficient trajectory optimization using the point that the dynamics of a deterministic system are uniquely determined by initial states and controls imposed over the time horizon of interest. To effectively implement this concept,the Hermite spline is adopted to interpolate the continuous controls and the system dynamics are integrated with corresponding control parameters in prior. As a result, the optimal control problem can be transcribed into a nonlinear programming problem which has no dynamic equality constraints and no intermediate states in its design variables. In addition, the paper proposes an efficient recursive Jacobian estimation technique and introduces a Jacobian transformation matrix to straightforwardly handle the general state constraints. Important properties of the present method are thoroughly investigated through its applications to the trajectory optimization for a soft lunar landing from a parking orbit, including the detailed analyses for the de-orbiting phase. The computed results are compared with those using the pseudo-spectral method to demonstrate an extreme outperformance of the proposed method in the aerospace applications over the traditional direct method.

1. Introduction

The Trajectory Optimization Problem(TOP)intends to obtain the trajectory and the corresponding control input while satisfying both the constraints and specific control objectives. The recent enhancement in computer performance allows a feasible numerical solution for TOP with the complex dynamical system and various efficient methods have been developed for that purpose. Among them, the indirect and direct methods are commonly used in real applications. The indirect method was known to transform TOP into a two-point boundaryvalue problem by applying the calculus of variation.1,2The indirect methods can provide an optimal solution,but it suffers from a relatively small radius of convergence.The direct methods3–7typically apply the specialized transcription techniques to transform TOP into a Nonlinear Programming problem(NLP), the design variables of which consist of all state and control parameters, defined at each collocation point. And,the system dynamics are transformed into the equality constraints. Thus, a large-scale NLP should be solved to get an optimized trajectory.In the last 20 years,the direct orthogonal collocation (or pseudo-spectral) method, which applies gauss quadrature points as collocation points, is a very popular.The Pseudo-Spectral(PS)4method,which uses a globally fixed nodes,has dense nodes at the boundary and sparse at the midpoint. For this reason, since the elements of the integration matrix at the boundary become smaller, the convergence performance at the boundary is decreased. Many research have been conducted to improve the convergence of pseudospectral method. Darby et al.8developed a variable loworder adaptive pseudo-spectral method which can adjusts both the mesh spacing and the degree of the polynomial on each mesh interval. Chai et al.9applied variable order pseudospectral method to an aeroassisted vehicle model.Patterson et al.10presented a ph mesh refinement method using Legendre-Gauss-Radau points.Liu et al.11,12presented an adaptive mesh refinement method using nonsmoothness detection and mesh size reduction. Ma et al.13,14applied a Hamiltonian-based adaptive mesh refinement strategy to the Lunar landing problem.Huang et al.15proposed a pk-adaptive mesh refinement of pseudo-spectral method using Legendre-Gauss-Lobatto points.

This paper proposes a new direct method that improves computational efficiency and convergence performance in boundary conditions. The system states in the deterministic system can be uniquely defined by initial states and controls imposed over a time horizon of interest. In a case when all intermediate states are determined by the system dynamics and the controls, the trajectory optimization problem can be transcribed without the states and the dynamic constraints.The present paper intends to implement this simple concept to the existing direct method and to demonstrate the associated usefulness in solving TOPs. If successfully implemented,the above concept can allow a much smaller size of the Karush-Kuhn-Tucker (KKT) system than that of the traditional direct method and may greatly enhance computational efficiency in solving TOP with a complex dynamical system.The system dynamics for aerospace applications are commonly represented by high-fidelity complex math models with relatively large number of states.16–20One of the present authors has studied on TOP of the rotorcraft and the effect of the fidelity level of rotorcraft models on computing time has been thoroughly investigated using the pseudo-spectral method.21,22Recently, one of the present authors has successfully applied the proposed method to the Category-A maneuver of the rotorcraft’s point mass model.23This paper follows this line of approach and the proposed implementation techniques for this purpose are collectively named as the Direct Dynamic-Simulation Approach (DDSA) throughout the paper.

Various numerical techniques to efficiently implement DDSA are proposed in this paper. First, the controls are parameterized using the Hermite spline interpolation,24with which the continuous controls over a time interval between two adjacent collocation points can be represented as the function of the control parameters defined at these two-end points.The dynamic simulation of the motion equations using the interpolated controls allows a straightforward establishment of the mentioned functional relations, with which the NLP can be formulated by the design variables consisting only initial states and control parameters. Secondly, the paper proposes a recursive algorithm for an efficient estimation of the state Jacobians over whole collocation points using the local Jacobians computed at each time segment.Thirdly,a Jacobian transformation matrix is defined to efficiently handle states and control constraints at collocation points. This Jacobian transformation matrix is used to transform the Jacobians for intermediate states into those for design variables(initial states and control parameters). Finally, the pseudo-spectral integrator23,25–27coupled with the fixed-point Piccard iterative method is adopted to compute the fully converged state solutions. This implicit integrator is extremely valuable in that it requires only a few iterations in computing the states with updated control parameters and in estimating new Jacobians using the finite difference formula.The resultant NLP is solved using the Robust Sequential Quadratic Programming(RSQP)28algorithm. Here, the KKT system is built by using the Broyden-Fletcher-Goldfarb-Shanno (BFGS)29algorithm to update the Hessian matrix and by applying the established a Jacobian transformation matrix.

The proposed DDSA was applied to the trajectory optimization for a Soft Lunar Landing(SLL)from a lunar parking orbit.Many research have been conducted for soft lunar landing problem using both indirect and direct method.The previous studies30–32for SLL typically adopted a three-phase approach consisting the de-orbiting, unpowered descent, and powered braking phases. The trajectory for the de-orbiting phase is extremely difficult to optimize because of its relatively short duration with a limited thrust. In such a case, the pseudo-spectral method suffers from extremely poor convergence with a fine distribution of nodes around the initial time.Also, the corresponding NLP typically shows too poor sensitivity to the shape of the de-orbiting thrust to accurately capture the optimum thrust. Therefore, most research mainly focused on the powered braking phase where the most fuel is consumed. Most of these studies assume the de-orbiting and the unpowered descent phase as Hohmann transfer. There are many studies on the trajectory optimization of the powered braking phase using the indirect33,34and direct35–40methods.Ref.33,34studied the perilune altitude33with minimum energy and the optimal phase angle34of the powered braking phase to maximize the final mass using the indirect method. Ref.35–39studied the lunar landing trajectory to minimize fuel consumption using a control parameterization35,36, the direct collocation37,and pseudo-spectral method38,39.Ref.13,14proposed the fuel minimization trajectory using a simultaneous dynamic optimization approach and an adaptive mesh refinement strategy.

There have been the researches30–32,40on de-orbiting phase of the SLL problem. Ramanan and Lal40studied the case of(A) powered landing phase from lunar parking orbit (B)powered landing phase from intermediate orbit (C) powered horizontal braking phase from intermediate orbit using the indirect method.

The general features of the solution for the fuel-optimal SLL problems can be found in the previous study performed by Hawkins.30As authors know,he is only one who optimized the SLL trajectory from a circular parking orbit without resorting to the peri-lune or intermediate height constraints in order to identify the undesirable characteristics in the predicted trajectory. He compared the results computed using the pseudo-spectral method with and without knots.The computed throttle has a bang-off-bang profile, which is characterized by the initial de-orbit burn, followed by an unpowered descent coast, and a final braking burn. He adopted the knotting technique in order to accurately capture the discontinuous change of the thrust and enforced the throttle to zero during the descent coast maneuver. In his high-resolution solution with knots, the durations of the de-orbit and final braking burns have been predicted around 0.0702 % and 9.2524 %of the flight time, respectively. He pointed out that the perilune height of the optimized unpowered descent orbit becomes negative and a collision with the Moon’s surface may occur even with a small delay in the braking burn. In addition, he thoroughly investigated the effect of the targeted peri-lune altitude ranging from-40 to 30 km with the 5 km interval on the optimized trajectory and compared the fuel penalty and maneuver duration times.Park et al.31solved the SLL problem from a parking orbit placed at the height of 100 km with specifying the starting altitude of the braking burn phase with 20 km. The durations of the de-orbit and final braking burns have been predicted around 0.1887 % and 16.9607 % of the flight time,respectively.As a result,it can be said that the formulation and solution strategy to obtain a collision-free trajectory with the Moon’s surface and to accurately capture the impulsive thrust during the de-orbiting burn phase are required to solve TOP for SLL.Therefore,an accurate prediction of the minimal fuel consumption during the landing phase may highly depend on the resolution around the on and off phases of the thrust.

For these reasons, the present paper thoroughly investigates the solution characteristics of SLL problem prior to the performance of rigorous comparative studies on achievable efficiency and accuracy with the proposed DDSA.TOP for the SLL problem is inherently a free final-time optimal control problem. The free final-time formulation may fail to obtain a converged solution due to poor sensitivity of the objective function to the final time.This point is addressed through trial analyses.In addition,the optimized trajectory with a relatively long period of the landing maneuver may unrealistically contact with the Moon’s surface before the spacecraft reaches its final landing point. After thorough investigations on various issues mentioned above, the paper defines a suitable formulation of SLL for the comparative studies on the numerical efficiency and accuracy of the proposed DDSA.

The structure of this paper is as follows.In Section 2,a theoretical background for the proposed DDSA is presented. In Section 3.1, the general solution features for SLL problem were thoroughly investigated, and the poor sensitivity of the free-final time SLL problem was addressed through trial analysis.In Section 3.2,the optimized solution with the fixed finaltime formulation for SLL problem was rigorously investigated to capture major underlying features. In Section 3.3, the optimized results with DDSA are compared to those using the traditional pseudo-spectral method, and an extreme outperformance of the proposed DDSA over the pseudospectral method has been demonstrated.Finally,Section 4 presents conclusive remarks of this paper.

2. Direct dynamic-simulation approach

This section addresses how DDSA differs from the traditional direct methods by using the following Bolza form of optimal control problem1and by comparing its major routines with those of the pseudo-spectral method.

Here, the initial and final state constraints, and the global inequality constraints are represented by ψ and g,respectively.Other constraints like the final state inequality constraints can be simply added in Eq. (1). The Mayer form best suits for DDSA from an efficiency point of view and it can be obtained using the following representation for the objective function.

Therefore, the resultant numbers of design variables and constraints become (n+m)(N+1)+1 and(n+Li)(N+1)+Le, respectively.

Whereas, DDSA divides a time horizon into several segments(4 segments in Fig.1)and collocation points are defined by each of connecting points and two-end points (square marks in the Fig. 1). DDSA integrates the system dynamics using the initial states x0and continuous controls u(t)interpolated with the control parameters vj; (j=0;1;∙∙∙;Nc) to get the states xj. Thus, the states at each of collocation points can be obtained using

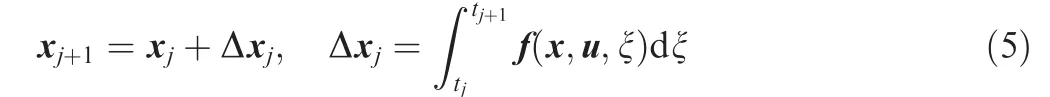
The state change Δxjover a time segment can be computed by applying any types of integrators and by using computational nodes distributed between two adjacent collocation points.

The result shown in Eq.(10)is extremely important from an efficiency point of view because xj+1depends only on the forward part of the control parameters (v0;v1;∙∙∙;vj+1), which allows an efficient recursive estimation of the Jacobians related to the design variables. This is the reason why the Hermite spline is adopted in the present DDSA. Using Eq. (9), the following relations can be derived.

Table 1 Pseudo-code for integrating the system dynamics over a segment [SystemDynamicIntg].

The states at all collocation points are computed using the moving-horizon framework,21–23,25–27where the initial states at each time segment are set by the converged state solution at the final computational node of the previous segment. The time integrator is intensively used in DDSA to update the states with the current iterate of the design variables and to compute the local Jacobians in Eq. (11). The changes in the design variables at each iteration and in their perturbations for the computation of the Jacobian matrices are typically small enough in most of later part of iterative NLP solutions.Therefore,once a converged state solution over all collocation points is obtained using the design variables defined in Eq.(17), the later solutions of Eq. (18) need only a few iterations.This is a great advantage of the present adoption of the implicit pseudo-spectral integrator.

The pseudo-code for the estimation of the initial-state and control Jacobians over a segment is listed in Table 2[StateControlJacobian]. It computes with ∂Δxj/∂xjand∂Δxj/∂vj; (j=0;1;∙∙∙;Nc), which are required for the recursive formula shown in Eq. (11). In a case when interpolating functions with the global support like the Lagrange polynomials are used for controls, every perturbation of controls requires the integration of the system dynamics over whole time-horizon to estimate the Jacobean matrices. Whereas, the integration over each segment and the application of Eq.(11) are enough to compute all required Jacobians in the present DDSA.

The number of design variables and constraints in the NLP transformed with the present DDSA can be counted by n+m(Nc+1)+1 and Le+Li(Nc+1), respectively. In a case when the same number of collocation points are used for both the pseudo-spectral and DDSA methods,the relative reduction in the size of the KKT system with DDSA can be estimated by 2nNc+n+1.Therefore,the proposed DDSA can outperform the traditional pseudo-spectral method especially when TOP with a dynamical system containing the relatively large number of states is analyzed using an extremely fine distribution of collocation points. Whereas, an efficient implementation of DDSA to a specific TOP needs some numerical trials to estab-lish the effect of the solution parameters listed in Table 3 on numerical accuracy and efficiency.

Table 2 Pseudo-code for the initial-state and control Jacobian over a segment [StateControlJacobian].

3. Applications

The trajectory for SLL from a parking orbit is optimized using the proposed DDSA with multiple-horizon framework to demonstrate how DDSA can contribute to the solutions of the aerospace TOPs with outperforming efficiency and accuracy over the traditional direct methods.Fig.2 shows the schematic view of the problem with the definition for the position,velocity, and thrust vectors of the spacecraft along the trajectory. The planar spacecraft motion40is approximated in a polar coordinate system as

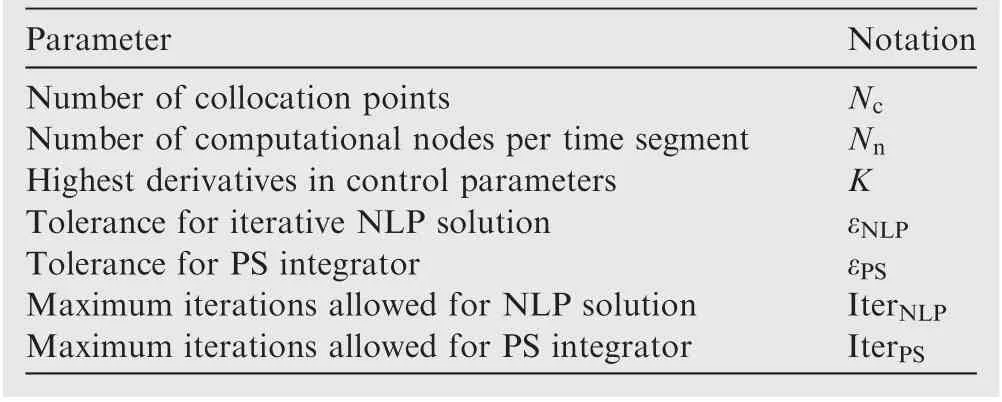
Table 3 Analysis parameters for DDSA.

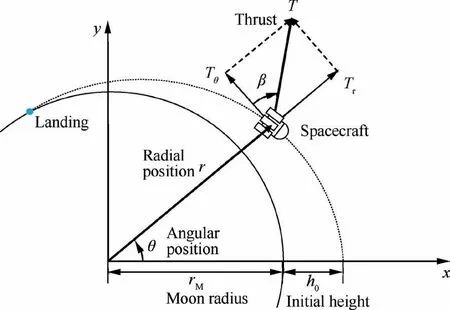
Fig. 2 Schematic view of the landing trajectory.

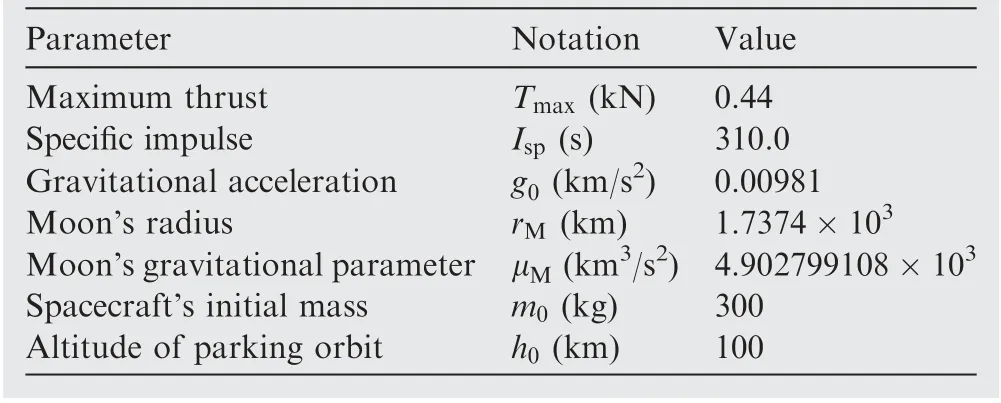
Table 4 Parameters of spacecraft and Moon.40

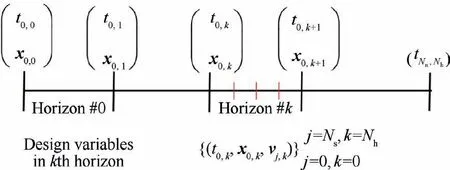
Fig. 3 Multi-horizon framework for DDSA.

There exist too many analysis parameters (shown in Table 3) for the applications of DDSA to address in detail their effects on the trajectory optimization. This paper selects those based on a series of rigorous numerical trials for various test problems.Here,the parameters selected for the purpose of this paper will be briefly introduced. The tolerance and maximum iterations allowed to integrate the motion equations are set by εPS=10-10and IterPS=100 for all applications throughout the paper. The transcribed motion equations shown in Eq. (3) is inherently a fixed-point problem. The implicit pseudo-spectral integrator developed in Ref.25has used this property and outperformed in the integration accuracy and efficiency over the explicit Runge-Kutta integrators.Using the pseudo-spectral integrator,the converged state solutions for DDSA can be obtained on most cases with less than 10 iterations except the first few NLP iterations. The NLP solution parameters, εNLPand IterNLPshould be selected considering the convergence properties of a specific problem.The Jacobian norm of the Lagrange function and the convergence in the objective function are considered for this purpose.The computational nodes over a segment are designated using seven Legendre-Gauss-Lobatto (LGL) points (Nn=7).

The order of the Hermite polynomials in Eq. (6) directly affects the computing time because the number of design variables in the transcribed NLP are nearly proportional to K.In a case when the higher-order Hermite polynomials (K≥2) are used, the sensitivity of the transformed NLP to the higherorder control parameters should be carefully investigated. As shown in Eq. (6), the mentioned sensitivity directly depends on the segment size Δtjand the area enclosed by each of the Hermite polynomials and τ-axis. With an extremely small Δtj,the NLP may become nearly insensitive to the higher order parameters, which may produce a nearly flat control distribution around each of collocation points because the first derivatives of a0(τ)and β0(τ)are zeros to meet Eq.(8)at collocation points.A simple scaling technique to increase the effective segment size proved to greatly enhance the sensitivity of the higher order control parameters from trial simulations. However, the present paper adopts a linear interpolation with(K=0) for all applications. The author would like to recommend the use of the lower order spline interpolation for an efficient analysis as far as possible. In addition, a linear interpolation can provide the required accuracy with a relatively fine distribution of collocation points without sacrificing numerical efficiency in most of trial applications of DDSA.

3.1. General solution features for the SLL problem

In previous study,the optimal solution of the SLL showed the result of touching the surface before the spacecraft reaches the final landing point.30With due consideration on the successful mission, many of previous studies typically imposed the perilune height constraint and implemented the resultant formulation using the knotting technique. Fig. 4 presents schematic distributions of the optimized thrust.Here,the descent maneuver is split into the de-orbiting, unpowered descent, and powered braking phases. The duration of the de-orbiting phase is relatively short, and the currently available direct methods may fail to provide the required resolution to analyze this phase. The Hohmann transfer approach and the ΔVmethod31–32have been typically adopted to avoid such resolution issue.

Another difficulty is related to the optimal control problem formulation.The final time is inherently free for the SLL problem.However,the initial guess for final time may greatly affect the solution convergency and the optimized results. Fig. 4 schematically represents this possibility when final time becomes long enough during an iterative solution process. In addition, the interim solutions for maneuver trajectories may frequently penetrate the surface of the Moon,which may cause a great embarrassment.In such cases,the solution history generally presents extremely poor convergence. A peri-lune approach adopted in Refs.30–32,40may be a good technique to provide a realizable trajectory without collision with the Moon’s surface.

This paper tries to show how the proposed DDSA is applicable to the SLL problem without resorting to the multi-phase peri-lune approach. First, the numerical difficulties in solving the free final-time formulation for the SLL problem with the single-phase approach are investigated using the following formulation.

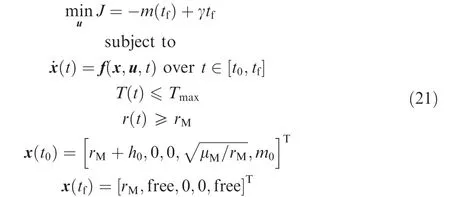
Here, the final time is added in the cost function with the parameter γ.The minimum-time problem can be obtained with a large value of γ, while the problem become an optimal-fuel one with γ=0. In addition, the global constraint r ≥rMis added to avoid the penetration into the surface of the Moon.

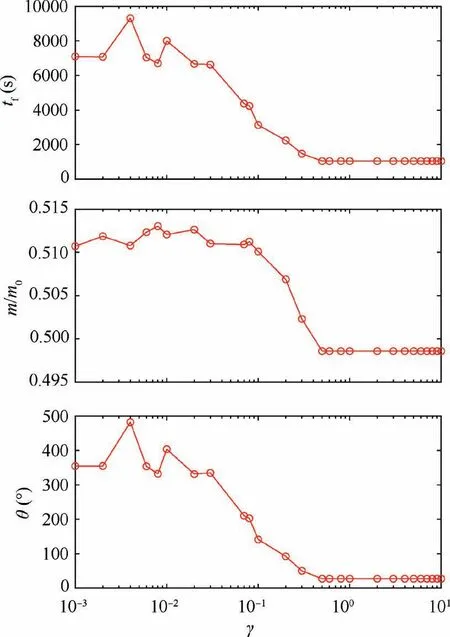
Fig.5 Converged optimal solution with variations in the weight parameter for final time.

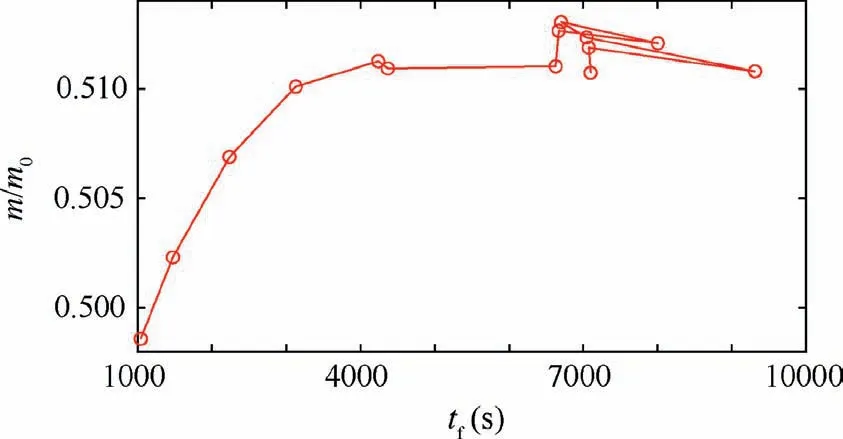
Fig. 6 Computed variations in the final mass.

The converged results with varying γ are summarized in Figs. 5–7. All analyses with γ ≥0.5 present the same minimum-time of around tf≈ 1000 s with approximately 50% mass reduction due to fuel expenditure. As γ approaches to zero, the solutions present only around 1–2% in the fuel savings compared to those obtained with the minimum time formulation with γ ≥0.5. Fig. 6 shows that the final mass curve becomes flat when the optimized final time is greater than 5000 s. This indicates that the final mass m(tf) becomes nearly insensitive (with ∂m(tf)/∂tf≈0)to the final time. Many of the present analyses with γ ≤0.5 showed poor convergence or even divergent behaviors due to such insensitivity. Also,Fig. 6 clearly shows that there may exist the different optimal-fuel solutions with the allowable tolerance of εNLP=10-5when tf≥6500 s.Fig.7 represents the computed optimal solutions with the different γ. As shown in the radial position,the constraint(r ≥rM)becomes active in the optimal trajectories computed with γ=0.08 and γ=0.03. In these two cases,the spacecraft flies along the Moon’s surface by consuming a negligibly small amount of fuel and with no ground clearance for a discernible time-period. The optimized solutions with varying γ are summarized in Table 5.

3.2. Optimized trajectory with the fixed final-time formulation

The SLL problem formulated in Eq. (20) is solved with variations in the fixed final-time to capture major underlying features of the optimized solutions. Then, the paper establishes a final time suitable for the comparative studies on the numerical efficiency and accuracy of the present DDSA. The results with different analysis parameters listed in Table 3 are compared to those using the pseudo-spectral method to demonstrate the relative advantages achievable with the proposed method.

All analyses are carried out in the multiple-horizon framework,where the number of time horizons and segments are set by Nh=8 and Ns=10 (81 collocation points), respectively.All collocation points are uniformly distributed,and the seven LGL quadrature points are allocated for computational nodes over each segment.The optimized solutions are obtained when the iteration reaches to its maximum allowable IterNLP=50000. The analysis results for tf≤3500 s are presented in Fig.8.The variations in the final mass and thrust well reflect the three distinct maneuver phases. The durations for the initial de-orbiting burn are less than 100 s for all solutions with tf≤3000 s. Since only less than three collocation points are located for this phase, the duration and shape of thrust control during the de-orbiting burn cannot be precisely captured with uniformly distributed 81 collocation points.

In case of tf≥4500 s as shown in Fig. 9, the optimized trajectories unrealistically penetrate the surface of the Moon.The optimized thrust distributions with tf=5500 s and tf=6000 s are nearly the same except a time-shift around 500 sec in the de-orbiting burn. This again validates the claim for the possibility of multiple solutions for the optimal control problem formulated with the free final-time. Fig. 10 compares the optimized final mass of the spacecraft. As final time is increased, the objective function in Eq. (20) gradually decreases. Therefore, even with TOP formulated with both the free final-time and global altitude constraint like r(t)≥rM, the optimized trajectory may contact with the Moon’s surface at some point in the middle of the landing trajectory. The optimized masses for these fixed final-time cases are summarized in Table 6.

A peri-lune approach can be adopted to effectively avoid such unrealistic trajectory solutions and it is typically implemented with the knotting technique to provide a high resolution for a rapidly varying trajectory solution. A peri-lune is typically prescribed with the height above ground in typical peri-lune approaches. The selections of this peri-lune height are commonly arbitrary (not optimized for the minimum-fuel consumption) in most literatures. Therefore, when this type of approach is adopted, the optimized trajectory from the parking orbit to the landing point may differ from the global fuel-optimal one. The peri-lune approach assumes that the spacecraft initially follows the Hohmann transfer orbit using an impulsive de-orbiting burn from the circular parking orbit.When the spacecraft arrives at the peri-lune (θ=π) of the Hohmann transfer orbit,the powered descent phase will be initiated.Therefore,the predicted angular position of the landing point is always greater than θLanding>π. Whereas, the present approach predicts the optimal landing positions smaller than π. The advantage of the peri-lune approach compared to the present global optimization is difficult to quantify because of extremely low sensitivity of the fuel expenditure. However,the peri-lune height should be carefully prescribed to obtain a realizable trajectory with the minimum fuel expenditure for an actual mission.

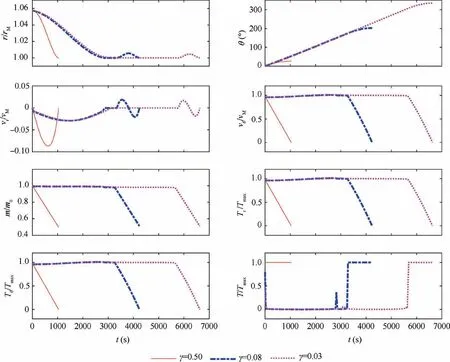
Fig. 7 Computed trajectories with varying weight parameter for final time.

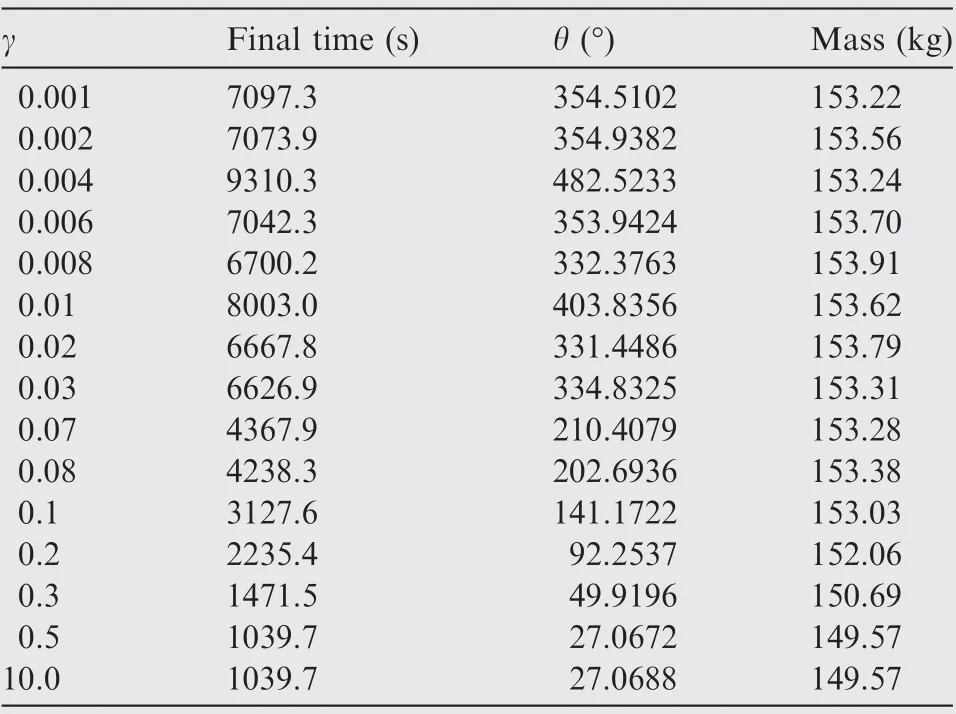
Table 5 Effects of γ on the optimal solution in the free finaltime formulation.

3.3. Comparative study on numerical properties of DDSA

This subsection intends to perform thorough investigations on the numerical performance achievable using the present DDSA.For this purpose,the SLL problem is formulated with the final time fixed as tf=2400 s, with which the optimized intermediate trajectory may maintain enough clearance above the Moon’s surface. First of all, there exist various options in distributing the numbers of time horizons (Nh) and segments(Ns) for DDSA, with which the number of collocation points is determined by NhNs+1. The effects of different combinations of Nhand Nson the numerical convergence are presented in Fig. 11. The analysis results applying different Nh=(1,10,60) with 61 collocation points are compared with that using the pseudo-spectral method. The Jacobian norm‖ΔL‖ of the Lagrange function is rapidly decreased in the early stage of iterations.Intermittent activations and deactivations of the inequality constraints for the thrust cause the oscillatory behaviors at the later part of iterations. Therefore,numerical convergence is judged using the time history of the mass.

All solutions using DDSA show nearly constant final mass after 105iterations. However, the final mass computed using the pseudo-spectral method continues to its gradual increase even after 1.5×105iterations.Also,it is smaller than the converged DDSA solutions.The analyses with DDSA include two extreme cases with Nh=1 and Nh=60.The transcribed NLP using Nh=60 needs applications of continuity conditions for states at each of connecting points of two adjacent horizon elements. Therefore, the corresponding number of equality constraints are the same as that using the pseudo-spectral method. Whereas, all these continuity conditions can be removed in the formulation with Nh=1, which allows much faster convergence than the analysis with Nh=60 in the early stage of iterations. The computing times required for different Nhs are compared in Fig.12,where all analyses are performed with the fixed 61 collocation points and IterNLP=1.5×105.The DDSA solutions with Nhless than 15 show no discernible differences in the computing time and around 3 times faster than the pseudo-spectral method.

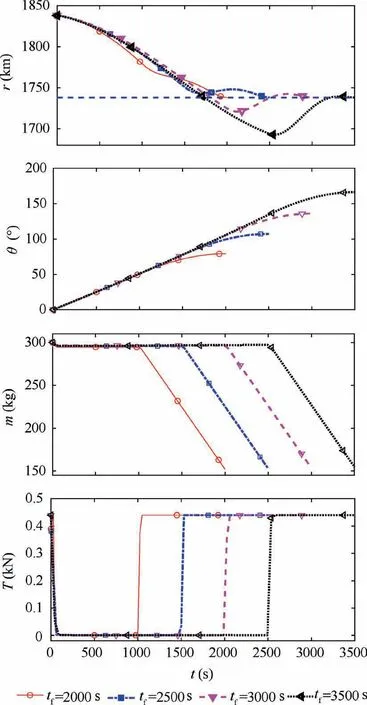
Fig. 8 Optimized trajectories with varying final times (tf≤3500 s).

Next applications are designed to clarify the effect of the number of collocation points on the resolution and computing time, where the collocation points for the pseudo-spectral method are identical to the computational nodes. All analyses are performed using the same iterative-solution parameters and terminated with IterNLP=1.5×105. The optimized thrusts for the de-orbiting phase with DDSA and the pseudo-spectral method are compared in Figs. 13 and 14,respectively. In a case when the pseudo-spectral method uses greater than 151 Collocation Points (CPs), it cannot perform even the first NLP iteration because the KKT system matrix is badly conditioned. The thrusts predicted with DDSA using greater than 121 collocation points well capture the impulsive nature of the de-orbiting phase,with which the gravity loss can be minimized.Whereas,the solutions with the pseudo-spectral method fail to provide such an impulsive de-orbiting thrust.There may exist two major root causes of poor resolutions and convergence in the pseudo-spectral solutions. First, the elements of the integration matrix corresponding to around the initial time are relatively small,which can degrade the sensitivity of the cost function to these initial thrusts. The other one is related to the characteristics of the SLL problem itself.The optimized trajectories spend less than around 2 percent of the initial spacecraft’s mass during the de-orbiting phase.Whereas,the required fuel mass for the powered braking phase presents around 50 percent. Therefore, the fuel expenditure during the de-orbiting phase has a relatively small contribution to the overall cost function, which again degrades the mentioned sensitivity with the pseudo-spectral method.

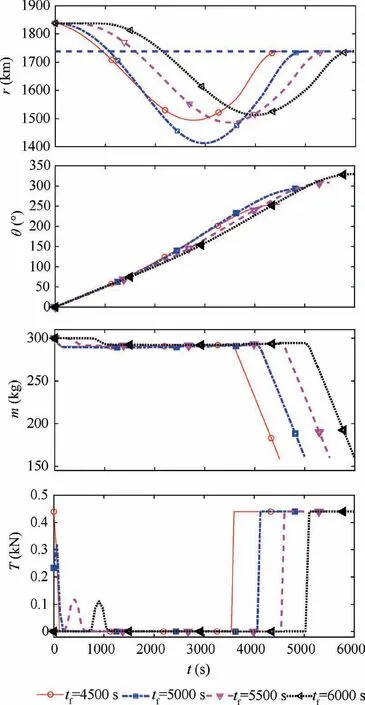
Fig. 9 Optimized trajectories with varying final times (tf≥4500 s).

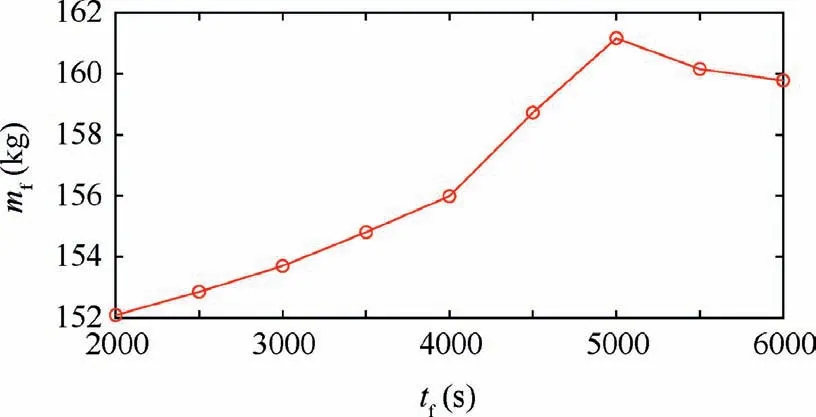
Fig. 10 Effect of final time on the optimized landing mass.

Table 6 Effects of tf on the optimal solution in the fixed final-time formulation.

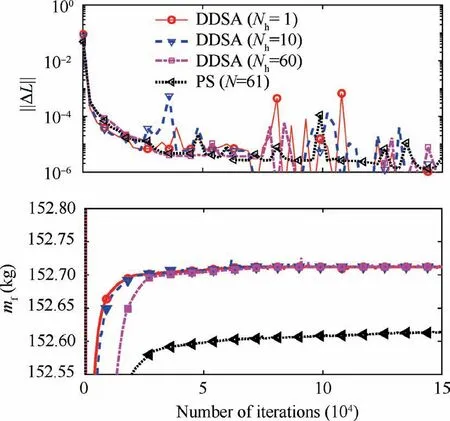
Fig. 11 Convergence histories of DDSA and PS solutions.

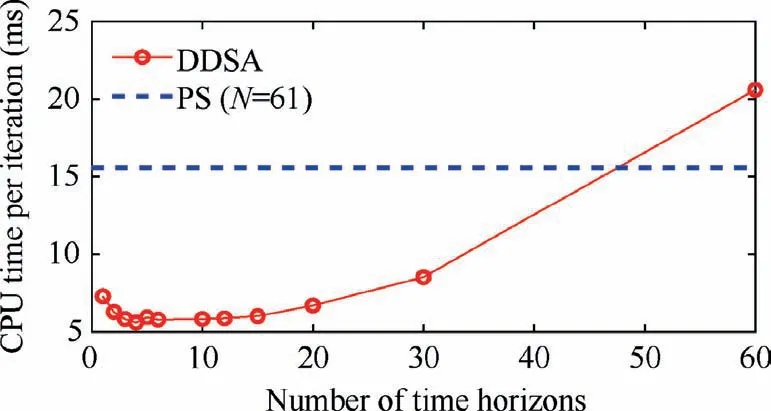
Fig. 12 Effect of the number of horizons on computing time.

The enlarged thrust solutions during the powered braking phase using two different approaches are presented in Figs.15 and 16, respectively. All solutions well present the impulsive engagement feature of the braking burn, which is captured with less than three collocation points in most of the solutions.The LGL quadrature points have a relatively coarse distribution around the midpoint of the time horizon. Therefore, resolution of the solutions with the pseudo-spectral method is much lower than that with DDSA which uses the uniformly distributed collocation points. This is another advantage enjoyable with DDSA.The pseudo-spectral method inherently uses a strict distribution of the quadrature points.Therefore,it needs a specialized technique to enhance the resolution like the mesh refinement method,3,8–15which says that the resolution cannot be enhanced without sacrificing computational efficiency. On the other hand, DDSA can use the arbitrarily distributed collocation points. Also, it has no limitations even in the application of the adaptive grid techniques. Therefore,we can claim that the resolution in the optimized solution can be greatly enhanced with DDSA while maintaining the same level of the computing time.

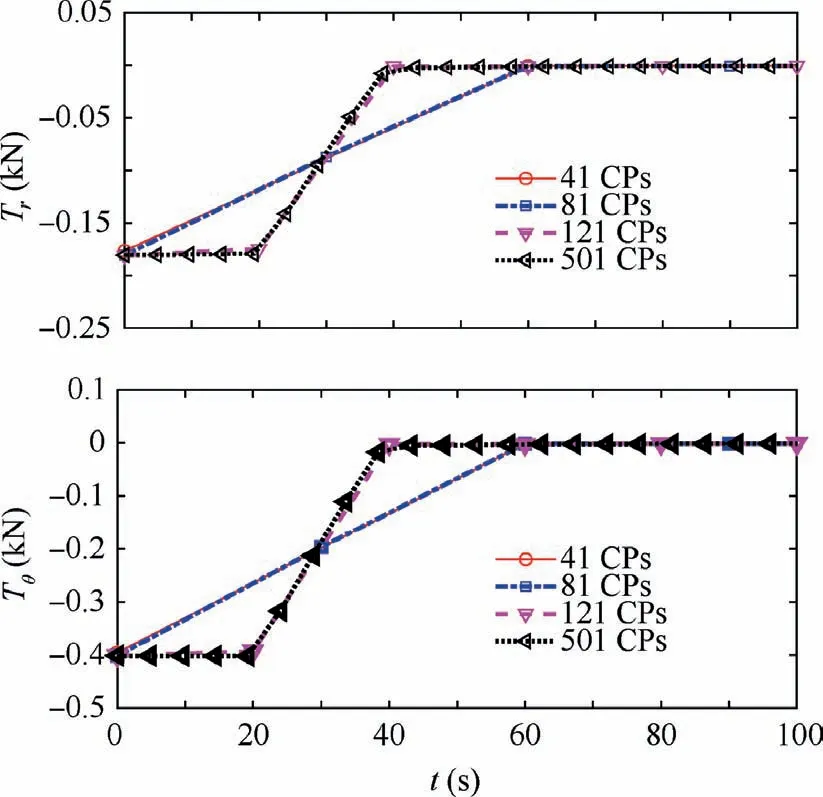
Fig. 13 Thrust distributions optimized with DDSA for deorbiting phase.

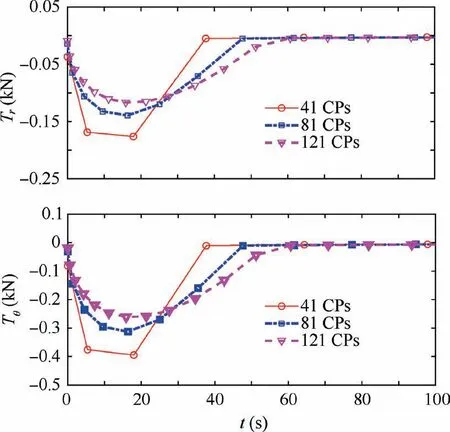
Fig. 14 Thrust distributions optimized with PS method for deorbiting phase.

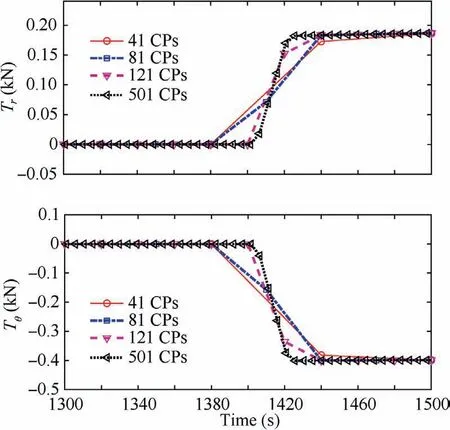
Fig. 15 Thrust distributions optimized with DDSA around at the start of powered braking phase.

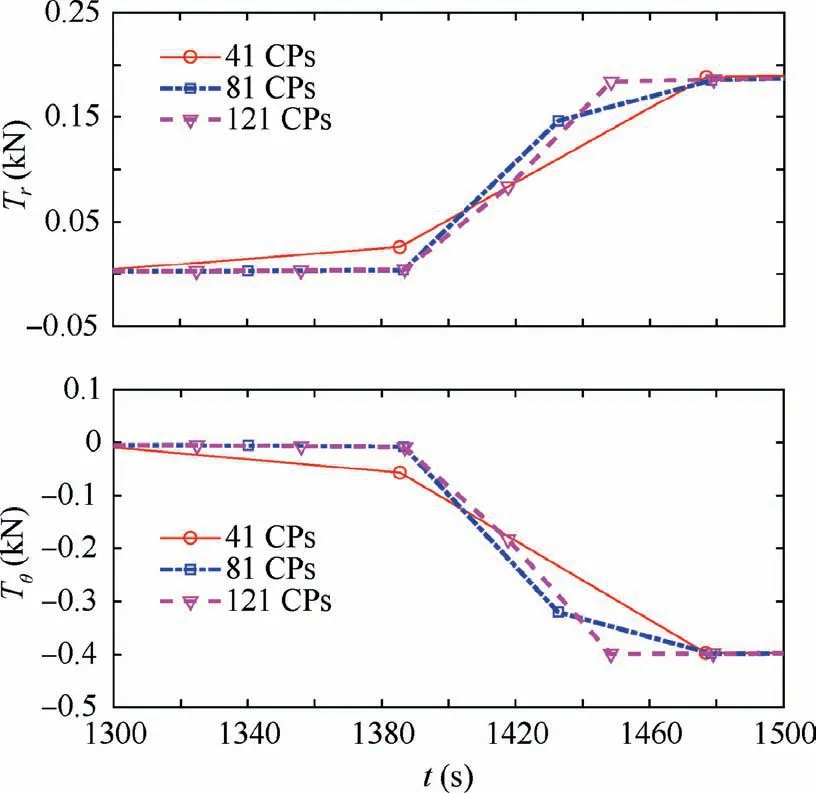
Fig. 16 Thrust distributions optimized with PS method around at the start of powered braking phase.

Computational efficiency achievable with DDSA is summarized in Table 7 and compared with that using the pseudospectral method. All analyses with DDSA are performed with 11 collocation points per each horizon and the desired total number of collocation points determines the corresponding number of the time horizons. The NLP formulated with DDSA has much less numbers of design variables and equality constraints than those with the pseudo-spectral method. Even with 41 collocation points, DDSA outperforms the pseudospectral method in the computing time and it can provide greater than 10 times faster solutions when more than 141 collocation points are used. Moreover, the pseudo-spectral method fails to provide a converged solution with greater than 201 collocation points due to the badly conditioned KKT system with extremely large number of unknowns. The solution with DDSA using 501 collocation points is presented in Fig. 17. The impulsive natures during both the de-orbiting burn and powered braking phases are clearly captured. The exit of the de-orbiting phase and the initiation of the powered braking phase are predicted to occur around 29.0 and 1413.5 s,respectively.The fuel expenditures during these phases are estimated with 295.7 and 152.7 kg, respectively.

4. Conclusions

A new direct method for the trajectory optimization has been proposed and its usefulness was demonstrated through a series of the trajectory optimizations for the soft lunar landing from a parking orbit. The present paper proposed the direct dynamic-simulation approach, with which the corresponding nonlinear programming problem could be formulated without the dynamic constraints and intermediate system states at the collocation points could be removed from the design variables.Thereby, the proposed method could provide the Karush-Kuhn-Tucker system, the size of which is much smaller than that of the traditional direct method.

The trajectory optimization problem for a soft lunar landing from a parking orbit with a minimum fuel expenditure has been selected to demonstrate the computational efficiency and resolution achievable using the present direct dynamicsimulation approach. For this purpose, the paper performed a series of trial analyses to determine a final-landing time,with which the optimized trajectories could maintain enough clearance from the Moon’s surface until the spacecraft softly lands.All trial solutions with the final times less than 3000 s showed three distinct maneuver phases consisting of the de-orbiting,unpowered-descent, and powered braking phase. And, thecomputed durations for the initial de-orbiting burn are less than 100 s for all solutions. In addition, it was demonstrated that there may exist multiple solutions and the analysis efficiency can be greatly degraded in a case when the trajectories are optimized with formulation with a free final-time.

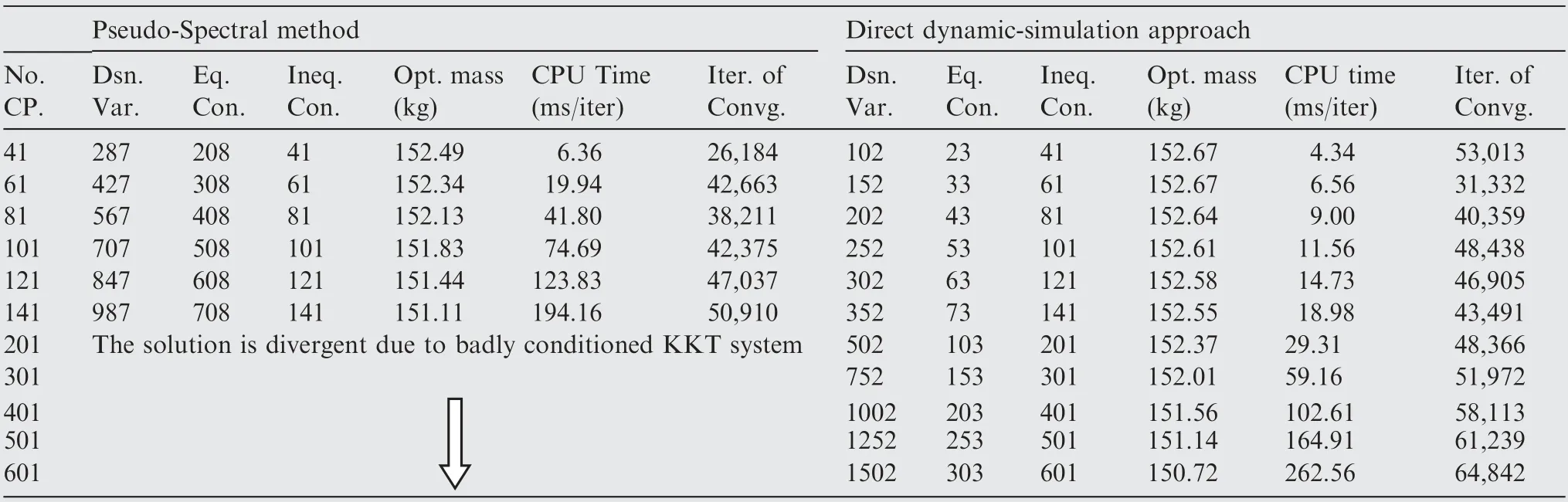
Table 7 Number of NLP parameters and CPU times with varying numbers of collocation points (εKKT <10-5).

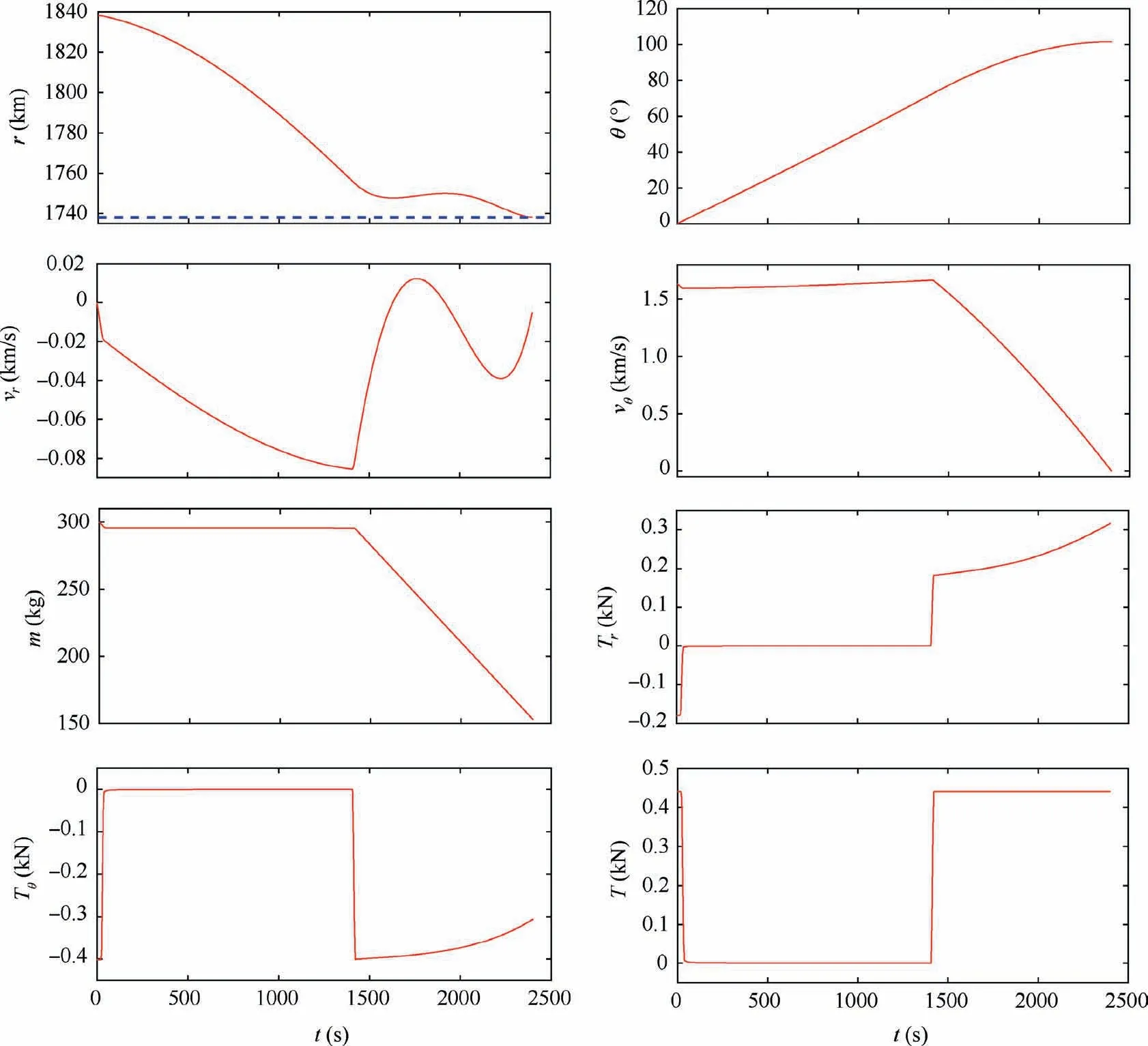
Fig. 17 Optimized trajectory solution with DDSA using 501 collocation points.

Rigorous comparative studies were performed to investigate the numerical properties of the proposed approach and to show its outperforming computational efficiency and resolution over the traditional pseudo-spectral method. All analyses for this purpose have been carried out with the final time of 2,400 s and the convergence of each solution were judged using the iterative variation in the final mass of the spacecraft. The results using 61 collocation points with variation in the number of time horizons showed that all analyses with less than 15-time horizons using the proposed method provided around 3 times faster convergence than the analysis using the pseudospectral method until 1.5×105iterations are performed. Furthermore, the pseudo-spectral method failed to provide the fully converged solutions while the converged solutions could be obtained after around 1.0×105iterations with the present method.The effects of the number of collocation points on the computational times and resolution in the optimized results were studied with evenly distributed 11 collocation points over each time horizon and compared to those computed with the pseudo-spectral method.For all prescribed number of the collocation points, the computing times for the present method were much shorter than the those for the pseudo-spectral method and the relevant ratios of them reached over 10 with 141 collocation points. The impulsive natures during both the de-orbiting burn and powered braking phases could be clearly captured with high resolution. Whereas, the pseudospectral method failed to provide such high resolutions in the optimized thrusts.From the results of present comparative studies,it can be concluded that the direct dynamic-simulation approach proposed in this paper can be effectively applied to many areas of the aerospace applications which require a high-fidelity math model with large number of the system states and high resolution in the optimized trajectory.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government(MSIT) (No. NRF-2020R1A2C2011955). Also, this research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF)funded by the Ministry of Education (No. 2020R1A6A1A03046811).