A two-step robust adaptive filtering algorithm for GNSS kinematic precise point positioning
Qieqie ZHANG, Luodi ZHAO, Long ZHAO
School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China
KEYWORDS Classification factor adaptive filtering;Global positioning system;Precise position holding;Robust filtering;Two-step filtering
Abstract In kinematic navigation and positioning, abnormal observations and kinematic model disturbances are one of the key factors affecting the stability and reliability of positioning performance. Generally, robust adaptive filtering algorithm is used to reduce the influence of them on positioning results.However,it is difficult to accurately identify and separate the influence of abnormal observations and kinematic model disturbances on positioning results, especially in the application of kinematic Precise Point Positioning(PPP).This has always been a key factor limiting the performance of conventional robust adaptive filtering algorithms. To address this problem, this paper proposes a two-step robust adaptive filtering algorithm, which includes two filtering steps:without considering the kinematic model information, the first step of filtering only detects the abnormal observations.Based on the filtering results of the first step,the second step makes further detection on the kinematic model disturbances and conducts adaptive processing.Theoretical analysis and experiment results indicate that the two-step robust adaptive filtering algorithm can further enhance the robustness of the filtering against the influence of abnormal observations and kinematic model disturbances on the positioning results.Ultimately,improvement of the stability and reliability of kinematic PPP is significant.
1. Introduction
Precise Point Positioning (PPP) is high-precision positioning technology based on precise satellite orbit and clock products.1It adopts pseudorange and carrier-phase observations, and sophisticatedly deals with various error terms at the same time.PPP has obvious advantages over differential positioning technology, such as working with one single receiver, no need to build a base station, unlimited operating distance, low cost,etc.2,3For those reasons, it has received widespread attention in recent years and become a heated research topic in the field of satellite navigation.4,5
For kinematic precise point positioning, it is usually challenging to maintain continuous and reliable high-precision positioning results due to the influence of parameter estimation with diverse approaches and the quality of observations. In order to obtain high-quality observations to avoid the influence of abnormal information on the positioning results, the observation data is usually preprocessed by real-time quality control,6such as model error correction,7cycle slip detection and processing,8and gross error detection and processing.9–12Nevertheless, some of cycle slips, gross errors and unmodeled errors in some observations,13which escape from the previous methods still exist and will affect the precision and reliability of PPP. Therefore, implementing robust processing in parameter estimation to further reduce the influence of abnormal information on the parameters estimation is great significant for improving the precision and reliability of the positioning results.In the field of satellite navigation and positioning,Kalman filtering is extensively used to obtain the optimal estimation of state parameters.14Since the performance of the filter is affected by the accuracy of the stochastic model and the function model,the optimal estimation of the state parameters can only be obtained if both are reliable.15However, in practical applications, various factors can lead to unsatisfactory filtering performance,16–18for example,the errors in state equations and gross errors in observations.
To improve the performance of Kalman filters, many researchers have conducted intensive research on adaptive filtering technologies.19–32For large errors in state models,researchers proposed fading filtering20–22and adaptive filtering.23They adjust the covariance matrix of the predicted state by the fade factor and the adaptive factor,respectively,so as to control the influence of the state model abnormalities on the filtering results. Since constructing adaptive factors is the key to adaptive filtering,researchers have made enormous research on how to obtain the best adaptive factors,and have proposed a variety of statistics for constructing adaptive factors,including state discrepancy statistic,variance component ratio statistic, and prediction residual statistic.24Aiming at gross errors or outliers in observations, Yang proposed a robust Kalman filtering algorithm based on robust M-estimation theory.24It constructs an equivalent weight matrix for observations to reduce the influence of abnormal observations on the filtering results.
In order to implement the adaptive processing of state model abnormalities and observation abnormalities, the robust adaptive filtering algorithm is put forward by combining the robust filtering and adaptive filtering.24,25Given the advantage that robust adaptive filtering can simultaneously restrict the influence of state model abnormalities and observation abnormalities on the filtering results, it has been broadly used and studied in kinematic navigation and positioning.26–29Varieties of improved approaches of robust adaptive filtering are derived from this base. Concerning the state models with different reliability levels, classification factors30and multiple factors adaptive filtering31have been developed. However,robust adaptive filtering can work ideally only if either observations or state model at a certain epoch is reliable.Due to the coupling of the detection of observation abnormalities and state model abnormalities, these two types of abnormalities are very likely to be confused and misjudged when the reliability of the observation and state model are unknown.32This will result in unreasonable equivalent weight matrix and adaptive factors, which may cause the gain matrix to be adjusted in the opposite direction where it should be and eventually lead to a more serious positioning deviation.So accurate identification and processing of the abnormal observations and kinematic model disturbances is crucial for robust adaptive filtering.
In short, this paper discusses and analyzes the problems of the conventional robust adaptive filtering algorithms,and proposes a two-step robust adaptive filtering algorithm for kinematic precise point positioning. Precisely, it includes two filtering steps: the first step keeps the kinematic model information out of consideration, and only the observation abnormalities are detected. Then the observations with the gross error are subjected to robust processing. In the second step,the kinematic model abnormalities are further detected and processed.To verify the proposed algorithm,simulation experiments with static data and real airborne experiments are conducted respectively.The results prove that the two-step robust adaptive filtering can further enhance the robustness against the influence of the observation abnormalities and the kinematic model disturbances on the filtering results and ultimately improve the stability and reliability of kinematic PPP.
2. Filtering models for kinematic PPP
The conventional Ionosphere-Free (IF) combination model is used as the observation model for precise point positioning.The IF combination observation equations for the code pseudorange and carrier-phase are as follows:
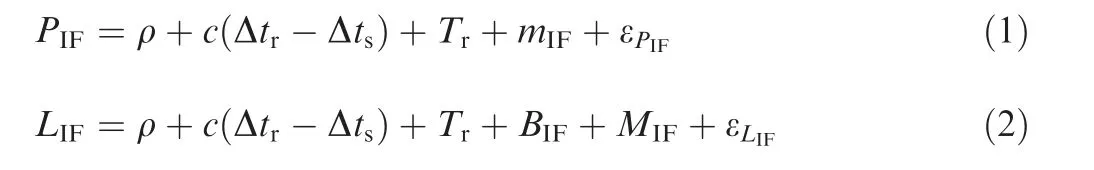
where PIFand LIFare the IF combination measurements of code pseudorange and carrier-phase. ρ is the geometric range between the satellite and the receiver antenna phase centers.c is the speed of light.Δtrand Δtsare the clock biases of receiver and satellite, respectively. Tris the tropospheric delay. BIFis the IF combined carrier-phase ambiguity. mIFand εPIFare the IF combined pseudorange multipath and observation noise, respectively. MIFand εLIFare the IF combined carrierphase multipath and observation noise, respectively.
In kinematic PPP, IF combination observation model and Constant Acceleration(CA)kinematic model are used to construct the observation equation and state equation. The state parameter vector is defined by

2.1. Observation equation
The observation equation of kinematic precise point positioning filtering model using the IF combination model can be expressed as

where,yk=[PIF;LIF]Tis the observation vector,which consists of the IF combination measurements of pseudorange and carrier-phase; vkmeans the measurement noise vector, and Rkis the corresponding measurement noise covariance matrix.
Linearizing the observation function vector h(x) to obtain the measurement matrix H:

where, σLand σPare the standard deviation of carrier-phase and code pseudorange measurement error, respectively; aσand bσare the carrier-phase error factor,and their default values are usually taken as aσ=bσ=0.003; s means the codepseudorange/carrier-phase error ratio, and its default value is 100.
2.2. State equation
According to the state vector shown in Eq. (3), the state parameters related to the PPP solution include position,velocity,acceleration,receiver clock bias,zenith tropospheric delay,and carrier-phase ambiguity. The CA model is utilized to describe the motion state of the carrier, the receiver clock bias is modeled as a white noise process,and the tropospheric delay and carrier-phase ambiguity parameters are modeled as a random walk process. The state equation is constructed as follows:

where σa,σclk,σtropand σBare the standard variance of acceleration process noise, receiver clock bias process noise, tropospheric delay process noise and carrier-phase ambiguity process noise, respectively; τ means the time interval.
3. Robust adaptive filtering algorithm
3.1. Operating mechanism
When both observations and state prediction parameters obey the polluted Normal Distribution,in order to restrict the influence of abnormal observations and abnormal predicted states on state estimation, the extreme condition can be constructed based on the free extreme principle, which is as follows

3.1.1. Construction of the equivalent weight matrix
When observations contain outliers, the equivalent weight matrix is constructed to reduce the weight of the observations with gross errors as

3.1.2. Construction of the adaptive factor
The IGG-III weight function model is also used to construct adaptive factor,26this is
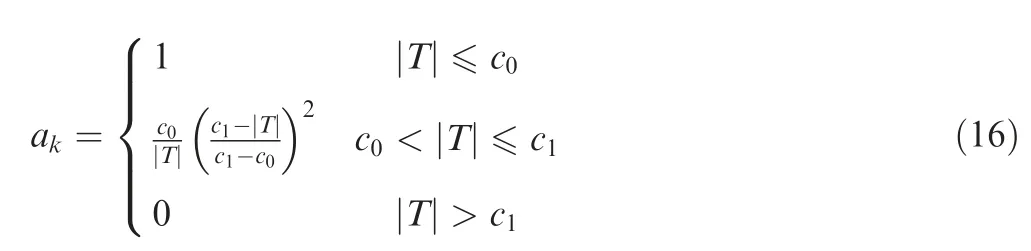
where,c0and c1are the detection thresholds.They are usually taken as c0=1.0 - 1.5 and c1=3.0 - 8.5,respectively;T is the discriminant statistic,Ref.24presents three discriminant statistics for constructing adaptive factors, including state discrepancy statistic, variance component ratio statistic and prediction residual statistic.Among them,the prediction residual statistic and the state discrepancy statistic are the most commonly used.
(1) The prediction residual statistic is calculated by

To avoid the rank defect of the single epoch robust least square solution of PPP, the carrier-phase ambiguity without cycle slip and tropospheric delay parameters are replaced by that of the previous epoch.
When the filtering algorithm is executed, the standardized residual statistics in Eq. (15) and the discriminant statistic T in Eq.(16)are used to detect abnormal observations and kinematic model disturbances. If an outlier is detected in a certain observation, an equivalent weight calculated by Eq. (15) is used to adjust the weight of the observation. If a disturbance is detected in the kinematic model, an adaptive factor is constructed according to Eq. (16) to adjust the covariance matrix of prediction states.
3.2. Problems analysis
Rewriting the robust adaptive filtering solution described in Eq. (11) to a recursive expression


However, for the conventional robust adaptive filtering,standardized residual statistics are usually used to detect abnormal observations. Since measurement residuals are related to not only measurement errors, but state estimation errors as well. In order to accurately identify the abnormal observations, reliable prediction state is essential. However,when prediction residuals are used to construct discriminant statistic in Eq. (17) to identify kinematic model disturbances,identification of kinematic model disturbances are supposed to take reliable observation as a premise. This is because the prediction residuals respond to the combined influence of measurement errors and state model errors, and the measurement residuals and the prediction residuals are coupled to the detection of abnormal observations and kinematic model disturbances. Therefore, it is difficult to accurately identify observation anomalies and kinematic model disturbances when the reliability of the observation and kinematic model are all uncertain.Alternatively,the robust least square solution based on the current epoch observations is adopted to construct the state discrepancy statistic as shown in Eq. (19), it can identify kinematic model disturbance avoiding the influence of abnormal observations. Nevertheless, conventional robust adaptive filtering base on state discrepancy statistic also has two main limitations. First, obtaining the robust least square solution requires redundant observations. Second, in order to avoid the rank defect of the single epoch robust least square solution of PPP, the carrier-phase ambiguity without cycle slip and tropospheric delay parameters are usually replaced by these parameters of the previous epoch. It also should be noticed that it requires that the carrier-phase ambiguity and tropospheric delay parameters are convergent and no cycle slips happen.
In the next section, a two-step robust adaptive filtering algorithm will be introduced to solve the above problems in the conventional robust adaptive filtering algorithms.
4. Two-step robust adaptive filtering
4.1. Classification factor robust adaptive filtering
The principle of adaptive filtering is to adjust the contribution of the prediction states to the state estimation by constructing an appropriate adaptive factor. For robust adaptive filtering with single adaptive factor, the prediction states are regarded as a whole, and a single adaptive factor is used to adjust the contributions of the prediction states to the state estimation.However, the state vector often includes different kinds of parameters, and the reliability of their state models varies as well. The classification factor robust adaptive filtering algorithm divides the state parameters into two categories according to the reliability of the state models, and constructs an appropriate adaptive factor for each class of state parameters30

4.2. Two-step robust adaptive filtering algorithm
Among the state parameters described in Eq. (3), the tropospheric delay and the carrier-phase ambiguity parameters without cycle slip are relatively stable, the random walk process is accurate to describe their state models. As for the position,velocity and acceleration state parameters described by the CA model,and receiver clock state parameter,due to the influence of various factors,it cannot guarantee that the state models used are consistently accurate. Therefore, according to the reliability level of the sate models, the state parameters can be divided into two categories as
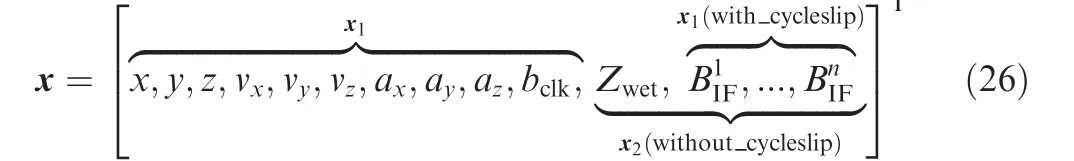
where x1is the first class of state parameters from the state models which includes position, velocity, acceleration, clock bias, and carrier-phase ambiguity with cycle slip, they are not always reliable; x2is the second class of state parameters from the state models which includes tropospheric delay and carrier-phase ambiguity without cycle slip, they are relatively accurate.
According to the principle of classification factor robust adaptive filtering, it can be known that adjusting the adaptive factor of a certain state parameter only changes the contribution of the state prediction information to the state estimation.When the adaptive factor is taken as axi=0, it indicates that the state prediction information of this class of state parameters will not affect the estimation of the state parameters;When the adaptive factor is taken as axi=1, it indicates that the influence of state prediction information on state estimation is not changed. In kinematic precise point positioning,since the state model of the second class of state parameters is accurately known,only the adaptive factor for the first class are supposed to be adjusted, with no need to adjust the adaptive factor for the second class (ax2=1). Based on the above analysis, this paper proposes a two-step robust adaptive filtering algorithm for kinematic precise point positioning. The flowchart is shown in Fig. 1.
As depicted in Fig.1,the two-step robust adaptive filtering algorithm includes two filtering steps. Explicitly, in the first step, the adaptive factor for the first class of state parameter is taken as ax1=0, and make an assumption that the second class of state parameter have completed convergence. Then the state estimation will not be affected by the abnormal values in the first class of state prediction information,only related to the quality of the observations.Therefore,at this step,only the abnormal observations are diagnosed, and the equivalent weight matrixwill not be affected by the abnormal values in the first class of state prediction information. During the second step, the adaptive factor for the first class of state parameters is first reset to ax1=1. Since the abnormal observations have been detected and processed after the first step,in the second step, only the state model anomalies of the first class of the state parameters need to be diagnosed, and the adaptive factors ax1constructed in this step filtering will not be affected by the abnormal observations. Consequently, the two-step robust adaptive filtering algorithm proposed in this paper can effectively identify observation abnormalities and state model abnormalities.
4.2.1. Global detection of observation abnormality
In Kalman filtering,the detection for observation abnormality usually uses the chi-square test based on prediction residuals,and its test statistic is
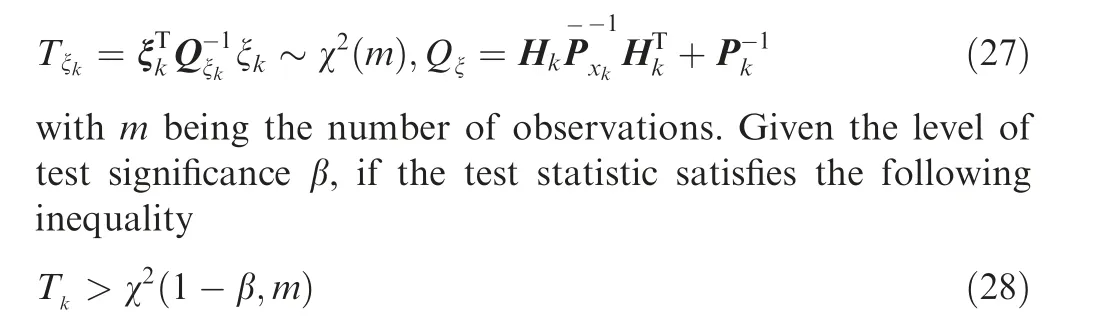
it is considered that there are probably gross errors in the observations,and then the equivalent weight matrixis constructed according to Eq. (14). In order to improve the sensitivity of detection, the significance level can be appropriately increased, which is taken as β=0.01 in this paper.
The chi-square test based on prediction residuals is a global test for observation abnormality and state model abnormality.Therefore, the diagnosis of the observation abnormality with the chi-square test statistics based on prediction residuals takes the reliability of the state model as the premise.In the first step filtering shown in Fig. 1, the chi-square test statistic based on prediction residuals can be rewritten as
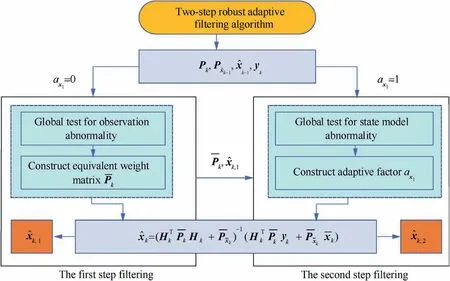
Fig. 1 Flowchart of two-step robust adaptive filtering algorithm.
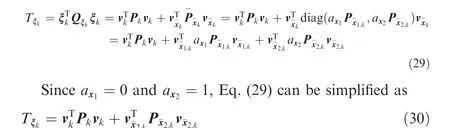
Eq. (30) indicates that in the first step filtering, the chisquare test statistic based on prediction residuals is not affected by the state model abnormalities of the first class of state parameters.
4.2.2. Global detection of state model abnormality
For the diagnosis of state model abnormality, the chi-square test based on predicted residuals can also be used for global detection. Since the observations have been subjected to robust processing in the first step filtering, it can be considered to be reliable. Therefore, the test statistic constructed by predicted residuals during the second step filtering will mainly reflect the error of the prediction states. The test statistic is defined as
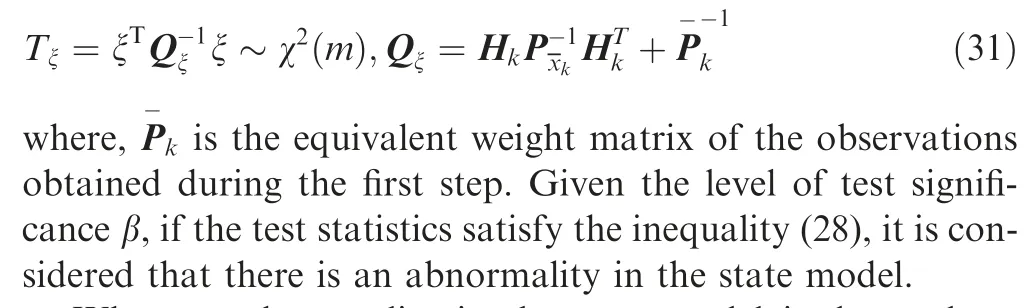
When an abnormality in the state model is detected, to reduce the effect of state model abnormality on the positioning results, the covariance matrix of prediction state is generally adjusted by an adaptive factor, thereby reducing the contribution of the prediction states to the positioning results. As in the state models, merely the kinematic model and the receiver clock bias model have errors, only the adaptive factor for the first class of state parameters need to be constructed. The equivalent covariance matrix of the prediction states can be calculated through Eq. (23), andis set as

where ^xk;1is the state estimation obtained by the first filtering step. Comparing Eqs. (19) and (32), it can be found that the least square robust solution x~k in Eq. (19) is replaced by ^xk;1.
5. Experiments and results analysis
5.1. Simulation experiments with static data
In order to verify the robustness of the two-step robust adaptive filtering algorithm, static observation data is first utilized to conduct the kinematic precise point positioning simulation experiment. The static GPS data was collected by NovAtel GPSCard on June 14, 2018 and was processed as follows: ①gross errors of 1 m and 20 m are randomly added to the carrier-phase and pseudorange observations, respectively, at epochs from 4000 s to 4100 s and from 6000 s to 6100 s to simulate the observation abnormalities; ②at epochs from 8000 s to 8100 s,a random velocity error with a magnitude of[–2 m/s,2 m/s] is added to the velocity parameters to simulate weak kinematic model abnormality; ③at epochs from 10000 s to 10100 s, a random velocity error with a magnitude of [–5 m/s, 5 m/s] is added to the velocity parameters to simulate large kinematic model abnormality; ④observation gross errors and velocity errors are added at epochs from 14000 s to 14100 s and from 12000 s to 12100 s to simulate the situation where two types of abnormality exist simultaneously. The following four schemes are performed for kinematic precise point positioning solution, respectively:
Scheme 1. Standard extended Kalman filtering algorithm for positioning solution (EKF).
Scheme 2.Conventional robust adaptive filtering algorithm,the prediction residuals are used to construct the adaptive factor (CRAKF_PRE).
Scheme 3.Conventional robust adaptive filtering algorithm,the robust least square solutions are used to construct the adaptive factor (CRAKF_RLS).
Scheme 4. Two-step robust adaptive filtering algorithm for positioning solution (RA2EKF).
In Schemes 2, 3 and 4, the test thresholds are taken as empirical value k0=1.0, k1=3.5, c0=1.0 and c1=5.0.The satellite cut-off angle is set to 7.5°.The measurement accuracy of pseudorange and carrier-phase observations is about 3.0 m and 0.03 m, respectively. Reference coordinates of the static station are used to evaluate the positioning errors of kinematic PPP. The results are shown in Fig. 2.
As depicted in Fig.2,at six periods of epochs with observation abnormalities and kinematic model abnormalities, all the positioning results of EKF in Scheme 1 show large deviations.In order to reduce the influence of observation abnormalities and kinematic model abnormalities on the filtering results,CRAKF_PRE in Scheme 2, CRAKF_RLS in Scheme 3 and RA2EKF in Scheme 4 are performed to detect and process both abnormalities.Figs.3 and 4 illustrate the detection results of CRAKF_PRE, CRAKF_RLS and RA2EKF for the kinematic model abnormalities and observation abnormalities.
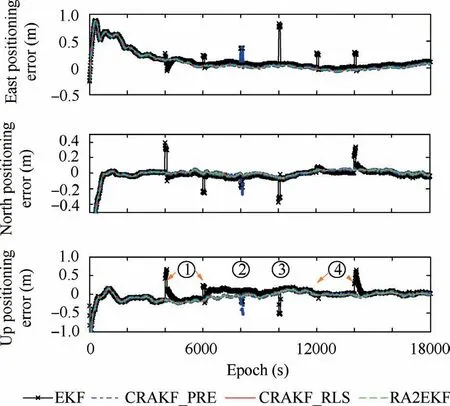
Fig. 2 Positioning errors of EKF, CRAKF_PRE,CRAKF_RLS and RA2EKF.
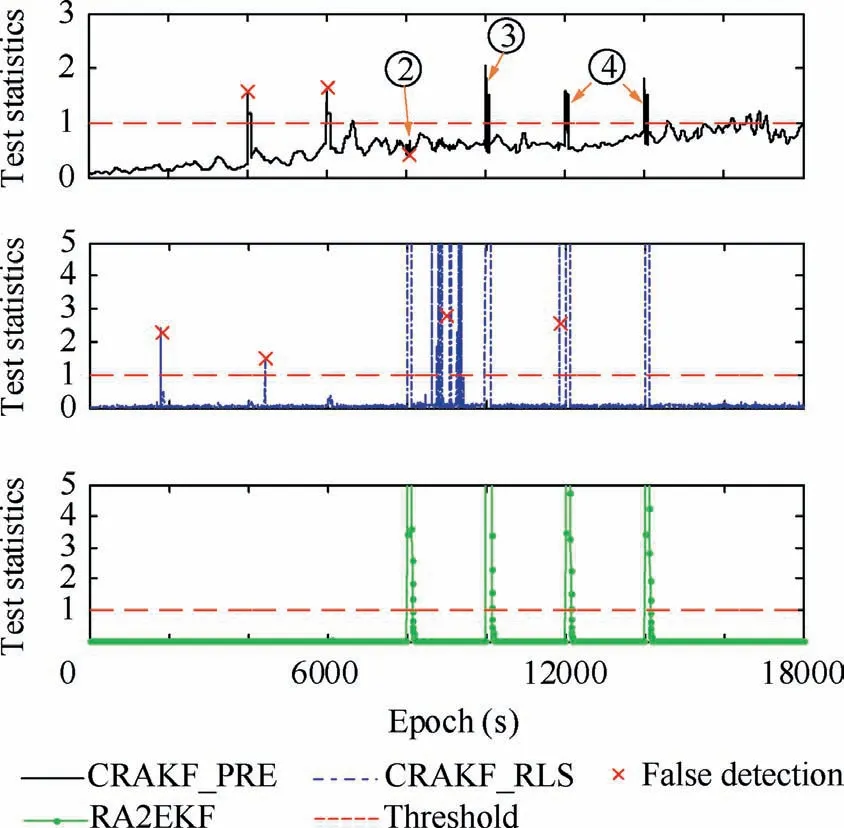
Fig. 3 Detection results of CRAKF_PRE, CRAKF_RLS and RA2EKF for kinematic model abnormality (static data).
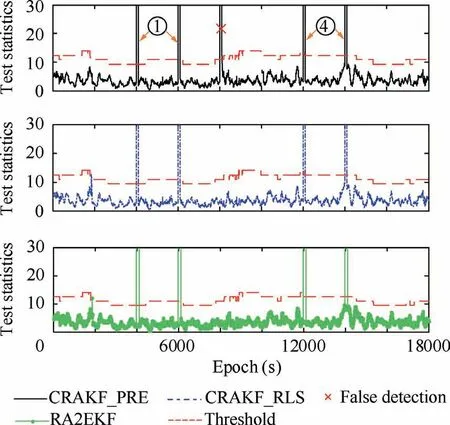
Fig. 4 Detection results of CRAKF_PRE, CRAKF_RLS and RA2EKF for observation abnormality (static data).
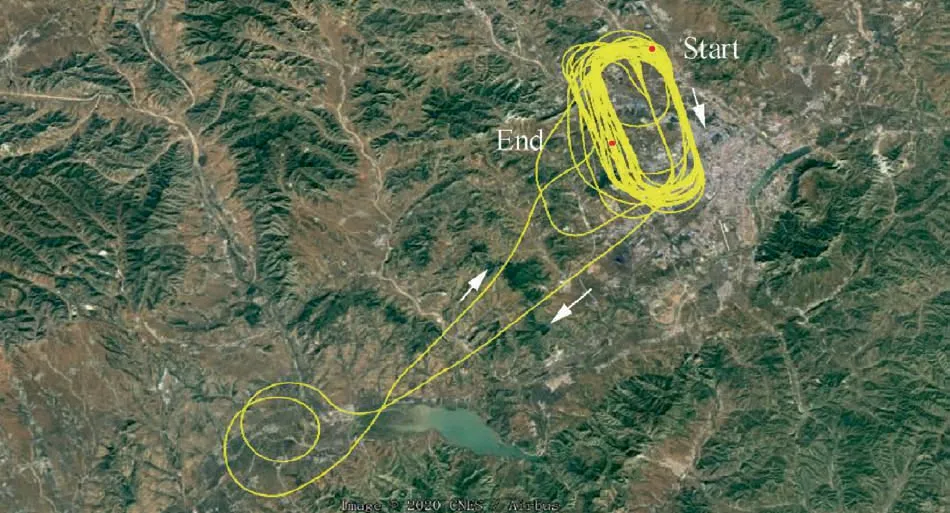
Fig. 5 Reference trajectory of airborne flight.
As can be seen from Figs. 4 and 5, although the CRAKF_PRE in Scheme 2 can detect the observation abnormality and kinematic model abnormality, false identification happens at some epochs. For example, at the epochs from 4000 s to 4100 s and from 6000 s to 6100 s, the observation abnormalities are also identified as kinematic model abnormalities. At the epochs from 8000 s to 8100 s, the weak kinematic disturbances are not detected. What’s worse, it is identified as an observation abnormality,which results in a larger positioning deviation as shown in Fig.3.At the epochs from 12000 s to 12100 s and from 14000 s to 14100 s,although the two types of abnormalities are detected,they could not be properly handled due to the interaction between observation abnormalities and kinematic disturbances.Even though the filtering results at the epochs from 12000 s to 12100 s and from 14000 s to 14100 s show no deviation in this experiment,there still lies a potential risk in adopting CRAKF_PRE when the two types of abnormality both exist. Because it fail to accurately balance the influence of the two types of abnormality on the filtering results. Compared with CRAKF_PRE, CRAKF_RLS and RA2EKF can correctly identify and process the six abnormalities as illustrated in Fig. 2. However, the detection results of observation abnormalities in Fig. 3 depicts that statistics of the CRAKF_RLS at multiple epochs are significantly larger than the detection threshold, which leads to the misjudgments of kinematic model abnormalities. Compared with CRAKF_RLS,RA2EKF is able to correctly identify and separate the observation abnormalities and kinematic model abnormalities. No matter observation abnormalities and kinematic model abnormalities both exist or not, RA2EKF can effectively restrict the influence of the two types of abnormality on positioning results.
5.2. Practical experiments with real airborne data
In order to further verify the actual performance of RA2EKF proposed in this paper,the practical experiments with airborne data are conducted. GPS data is collected on Aug 31, 2018 by the SPAN GNSS/INS receiver with a sampling frequency of 1 Hz. The reference trajectory is shown in Fig. 5, which is acquired in the differential GNSS positioning mode by the post-processing software NovAtel IE 8.70. It should be noted that the observation data in a good quality (no obvious outliers)and no obvious kinematic disturbances happened during the flight. The measurement accuracy of pseudorange and carrier-phase is about 2.0 m and 0.02 m, respectively. In order to verify the performance of the RA2EKF, ①gross errors of 1 m and 20 m are randomly added to the carrier-phase and pseudorange observations in the three periods, epochs from 2000 s to 2100 s, from 6000 s to 6100 s, and from 10000 s to 10100 s to simulate the observation abnormalities; ②only three visible satellites were utilized at epochs from 4000 s to 4100 s and from 8000 s to 8010 s to simulate the insufficient observations;③standard variance of process noise of accelerations are set as a stricter value (σa=10–2m/s2) to simulate kinematic model abnormalities.
With the elevation mask angle of the satellites is set as 7.5°,EKF, CRAKF_PRE, CRAKF_RLS and RA2EKF are utilized for PPP solutions. Fig. 6 illustrate the East, North and Up positioning errors, respectively. Fig. 7 as well as Fig. 8 show the detection results of CRAKF_PRE, CRAKF_RLS and RA2EKF for observation abnormalities and kinematic model abnormalities. Moreover, the statistical results of positioning errors of the four filtering schemes are listed in Table 1.
As illustrated in Fig.6 and Table 1,the statistical results of positioning errors of kinematic PPP in the three directions(East, North and Up) using EKF, CRAKF_PRE,CRAKF_RLS and RA2EKF filtering algorithms are (1.457,1.236, 2.566) m, (0.742, 0.530, 1.395) m, (0.371, 0.326, 1.061)m, and (0.320, 0.207, 1.001) m, respectively. Among the four filtering algorithms,the positioning results of EKF are the disappointing. The positioning result of EKF shows extensive fluctuations at most epochs due to the influence of kinematic model disturbances.
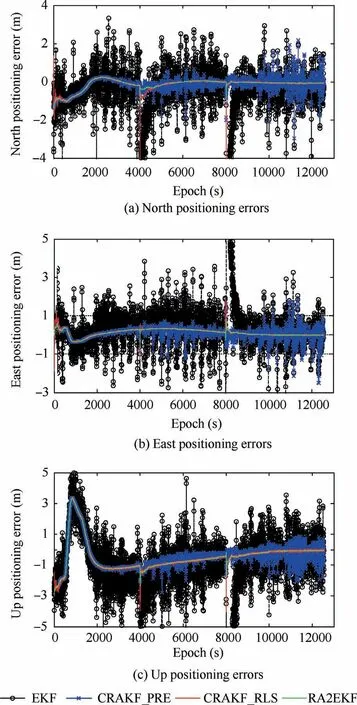
Fig. 6 Positioning errors of EKF, CRAKF_PRE,CRAKF_RLS and RA2EKF in direction of East,North and Up.
Compared with EKF,the accuracy and stability of the positioning results using CRAKF_PRE, CRAKF_RLS and RA2EKF filtering algorithms are significantly improved. The positioning accuracy in the three directions of (East, North and Up) are enhanced by (49%, 57%, 46%), (75%, 74%,59%) and (79%, 83%, 61%), respectively.
Among CRAKF_PER, CRAKF_RLS and RA2EKF,CRAKF_PRE has a slightly lower sensitivity to the detection of kinematic model abnormalities and fails to accurately process the weak kinematic disturbances, which causes deviation in positioning results at most epochs. Besides, the statistics of CRAKF_PRE remain rather small at most epochs as depicted in Fig.7.In addition,owing to the influence of observation anomalies in the three periods (epochs from 2000 s to 2100 s, epochs from 6000 s to 6100 s and epochs from 10000 s to 10100 s), the prediction residual statistics of CRAKF_PRE are obviously too large, which results in misjudgment of the kinematic model abnormalities.
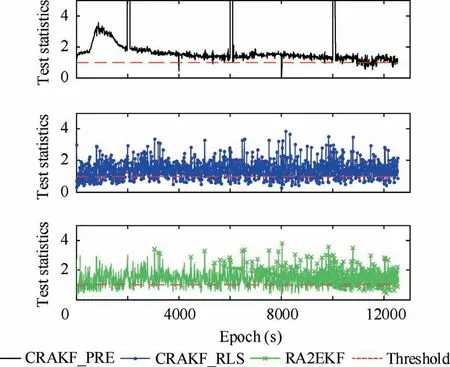
Fig. 7 Detection results of CRAKF_PRE, CRAKF_RLS and RA2EKF for kinematic model abnormality (real airborne data).
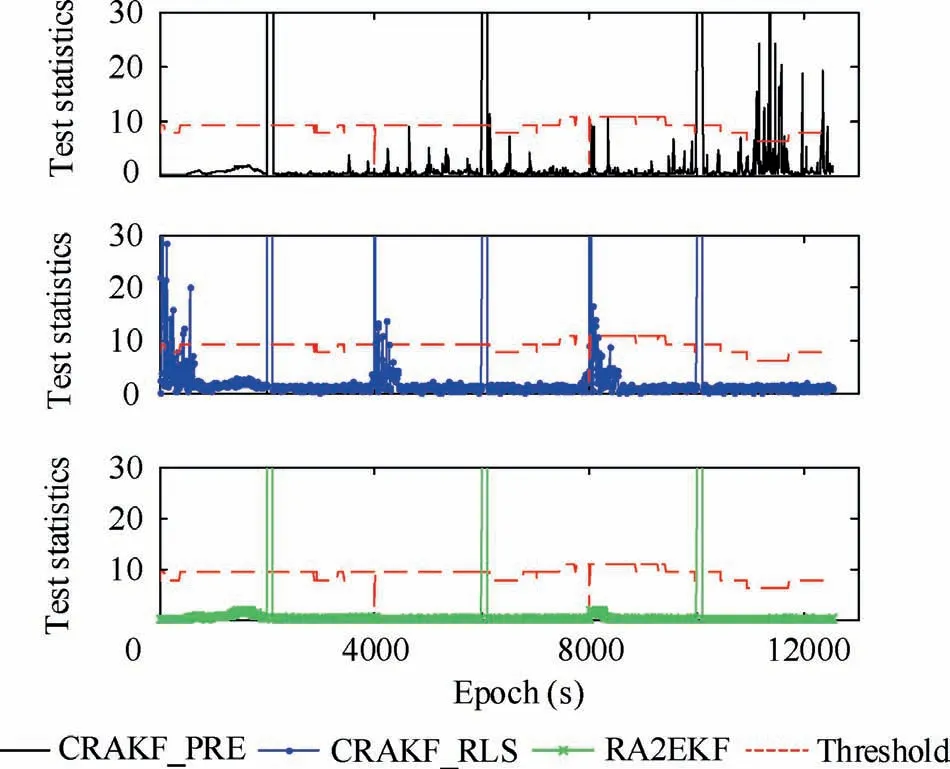
Fig. 8 Detection results of CRAKF_PRE, CRAKF_RLS and RA2EKF for observation abnormality (real airborne data).
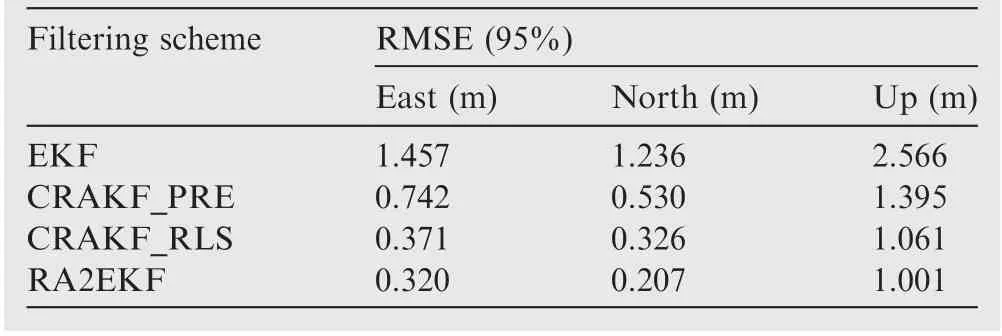
Table 1 Root Mean Square Error (RMSE) of four filtering schemes for kinematic PPP.
Compared with the CRAKF_PRE, CRAKF_RLS is able to correctly detect and deal with observation abnormalities and kinematic model disturbances at most epochs. With a smoother positioning performance, the positioning accuracy has been improved by 0.371 m, 0.204 m and 0.334 m in the direction of East, North and Up, respectively. However,Fig. 8 indicates that the positioning results of CRAKF_RLS have obvious fluctuations due to the misjudgment of the observation abnormalities in the initial convergence stage of PPP.Moreover, at the epochs from 4000 s to 4010 s and from 8000 s to 8010 s,CRAKF_RLS fails to detect kinematic model abnormalities, and misjudged the observation abnormalities due to the insufficient observations, which lead to huge deviations in the positioning results.
After further comparison of the positioning results of CRAKF_RLS and RA2EKF, it is obvious that RA2EKF has the smoothest positioning performance and the smallest positioning errors. Compared with CRAKF_RLS, the positioning errors in the direction of East, North and Up are reduced by 0.051 m, 0.119 m and 0.060 m, respectively. Moreover, the detection results of RA2EKF in Figs. 7 and 8 imply that RA2EKF can accurately identify and process the two types of abnormalities at the whole epochs.At the initial stage and the epochs with insufficient observations, a favorable robustness can also be realized, as the RA2EKF reduces the influence of unconverged carrier-phase ambiguity and tropospheric delay parameters in the first step filtering. In addition,thanks to the advantage of Kalman filter that it is not limited by the number of observations, RA2EKF can still work well with insufficient observations.
6. Conclusions
A novel two-step robust adaptive filtering algorithm for kinematic precise point positioning is proposed in this paper. The following conclusions can be obtained according to the theoretical analysis and experimental results:
· Compared with CRAKF_PRE filtering algorithm,CRAKF_RLS and RA2EKF have higher detection sensitivity for kinematic model abnormalities. They are able to detect and identify abnormalities in observations and kinematic models in the case the reliability of the observation and kinematic model are uncertain.
· Compared with CRAKF_RLS filtering algorithm,RA2EKF can be implemented under the framework of the original Kalman filter, saving the trouble to perform the calculation of additional least squares, so it has higher computational efficiency. In addition, the estimation of state parameters in RA2EKF makes it possible to avoid the situation that the CRAKF_RLS cannot work due to the rank defect of the robust least square solution caused by insufficient observations or cycle slips and allow RA2EKF show greater robustness than CRAKF_RSL in the case tropospheric delay and carrier phase ambiguity parameters are not converged.
Summarily, two-step robust adaptive filtering proposed in this paper combines the advantages of CRAKF_PRE and CRAKF_RLS, which can further enhance the stability and reliability of kinematic PPP compared with the conventional robust adaptive filtering algorithms. Nevertheless, it should be noted that RA2EKF has the same shortcoming as the CRAKF_RLS, which, if the observation abnormalities are not accurately preprocessed, will lead to a large deviations in the least square robust solutions or in the first step of filtering and eventually affect the accurate detection of kinematic model abnormalities.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
We extend our deep gratitude to Zhao Luodi for her contributions in putting considerable time and effort into completing and revising this paper. This study was co-supported by the National Natural Science Foundation of China (No.41874034), the National key research and development program of China (No. 2016YFB0502102), the Beijing Natural Science Foundation (No. 4202041), and the Aeronautical Science Foundation of China (No. 2016ZC51024).
 CHINESE JOURNAL OF AERONAUTICS2021年10期
CHINESE JOURNAL OF AERONAUTICS2021年10期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Direct dynamic-simulation approach to trajectory optimization
- A strong robustness open-circuit fault diagnosis strategy for novel fault-tolerant electric drive system based on d-q-axis current signal
- Nonlinear vibration response characteristics of a dual-rotor-bearing system with squeeze film damper
- Ground maneuver for front-wheel drive aircraft via deep reinforcement learning
- Numerical simulation of a UAV impacting engine fan blades
- Recent advances in precision measurement &pointing control of spacecraft
