采坑区冲沟演变影响下管道埋深预测
孙志忠, 任皓晨, 张满银, 王生新
(甘肃省科学院地质自然灾害防治研究所, 兰州 730000)
自改革开放以来,中国经济持续高速增长,基础设施建设突飞猛进。为满足建设期间用砂市场的巨大需求,于河道、沟道、山前冲洪积扇等区域进行了频繁、密集、无序的采砂活动[1]。滥采乱挖、过度开采、采后未治理现象十分严重,其遗留的采坑、废弃砂石堆等采砂痕迹改变了区域微地貌形态,影响水流主流方向及河(沟)道行洪,加剧坡面水毁区局部冲刷,不仅为区域内第三方施工埋下安全隐患,而且严重威胁桥梁基础结构物、油气管道线路等工程安全,同时对区域生态环境产生负面影响[2-5]。鉴于此,许多国家出台规范对新采坑最大开挖深度、面积及其与护堤、穿(跨)越工程的最小距离等进行了相应的规定[6-7]。河西走廊铁路、公路、管道工程沿线分布较多历史采坑,且在长期间歇性水流冲刷作用下,采坑边缘溯源侵蚀冲沟持续发育,潜在危险较大[8]。研究干旱、半干旱气候区冲洪积扇既有采坑演变过程,尤其对穿越段浅埋长输油气管道安全运营具有重要的意义。
当前,中外学者主要聚焦于常年性流水河道采坑变形、水砂运动机理等方面的研究,而针对山前冲洪积扇区间歇性水流作用下的采坑演变过程及其对人类工程的影响研究较少。李健等[9]利用有限体积法建立河道平面二维水流泥沙数学模型,提出了采坑对流场及地形的干扰程度与离采坑的距离、采坑的深度和面积大小以及来水来沙情况有关。毛劲乔[10]应用三维水流数学模型模拟矩形采坑局部流场、切应力等参数的分布情况,分析采坑产生的次生流现象及其对采坑横向扩展的作用。于合理等[11]依托美国陆军工程兵团工程水文中心开发的河道水利计算程序(river analysis system,HEC-RAS)模块进行数值试验,得出长浅型采坑比短深型采坑更能促进河床下切,且随着与采坑距离的增大,溯源侵蚀逐渐尖灭。李付军等[12]通过动床模型试验研究季节性河道上采坑对铁路桥梁的影响。可见,常年性流水河道内频繁的采砂活动及采坑使原有河床局部变形,破坏了既有的水砂运动平衡,同时水流流态变化引起面状溯源侵蚀,最终导致采坑及邻近区域河床全面调整。然而,冲洪积扇区采坑演变是在季节性洪流作用下呈间歇性,其溯源侵蚀以沟蚀为主,且持续时间较长,与常年性流水河道内采坑演变过程具有较大的差异性。齐梅兰等[13]通过水槽试验与数值计算,提出了采坑引起的溯源冲刷对其影响范围内水下结构物的总冲刷的贡献度最高可达80%。司鹏飞等[7]基于已有学者关于采坑冲刷深度等迁移变量经验公式研究基础上,提出穿(跨)越工程上游采砂安全距离的计算公式。64-1修正式、Lacey公式、谢鉴衡公式、王兆印冲刷公式等均广泛应用于管道穿越河流设计,但由于河床冲淤变化复杂,影响因素较多,参数取值不同导致计算结果存在较大的差异性[14-15]。洪积扇采坑区溯源侵蚀冲沟历经多次冲刷形成,其冲刷流量、冲刷时间等参数多变,且不易获取,故直接应用上述河床冲刷经验公式存在困难。
现以嘉峪关市黑山南麓洪积扇既有采坑及穿越段并行油气管道为研究对象,通过对采坑区溯源侵蚀冲沟冲刷长度、冲刷比降、冲刷深度、沉积厚度等进行调查与测量,分析冲沟溯源侵蚀与沟床回淤演变过程,建立管道埋深预测模型,并进行实例验证。研究成果不仅为在役管道穿越采坑区风险评价与水毁灾害防治提供理论依据,而且为拟建管道穿越采坑区选线提供技术参考。
1 材料与方法
1.1 研究区概况
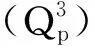
既有采坑主要为G30连霍高速建设期取土形成,迄今已十余年,其平面近似矩形,长约400 m,宽150 m,深4 m,面积约6×104m2,库容约2.4×105m3。管道位于采坑上游,二者呈并行状态,其中管道Ⅱ与管道Ⅲ为在役管道,管道Ⅰ为拟建管道。
1.2 调查、测量
采用区域调查、采坑区地形测绘、冲沟测量、坑探相结合的方法,研究采坑区冲沟演变过程。利用无人机、载波相位差分技术(real-time kinematic,RTK)测绘研究区地形地貌,确定洪积扇、采坑、冲沟等与并行管道的空间关系,并测量冲沟深度、宽度、比降等基本特征参数。采坑区累计调查溯源侵蚀冲沟5条,编号依次为G1~G5;其中G1、G5冲沟自沟口起,沿沟床间隔25 m布设探坑1处;G2~G4冲沟因沟床狭窄暂未布设探坑,如图1(a)所示。T1探坑长2 m,宽0.6 m,深2.5 m;T2探坑长2 m,宽0.6 m,深1.6 m;T3~T14为圆形探坑,直径0.6 m,深0.3~2 m不等,如图1(b)、图1(c)所示。研究区地形地貌、溯源侵蚀冲沟及探坑分布如图2所示。

图1 冲沟与探坑Fig.1 Gullies and test pits
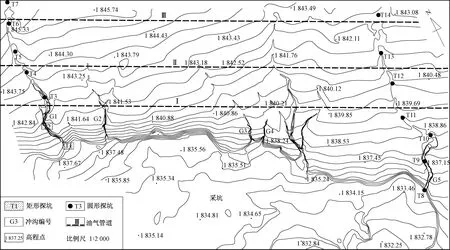
图2 研究区地形地貌及探坑分布Fig.2 Geomorphologic and distribution of test pits in the study area
2 采坑区管道埋深预测模型构建
2.1 采坑区溯源侵蚀冲沟演变过程
在间歇性水流作用下,洪积扇采坑区冲沟演变过程包括溯源侵蚀和沟床回淤两个连续的阶段。在野外调查基础上,假定沟床侵蚀面与回淤面均为平面,其冲刷比降和回淤比降均呈线性变化;忽略沟口沉积层厚度对沟床冲刷比降的影响,考虑其对沟床回淤比降的作用;侵蚀临界是溯源侵蚀阶段的终点,也是沟床回淤的起点;采坑底部均匀沉积,且不发生局部侵蚀。依据上述假设条件,采坑区溯源侵蚀冲沟演变简化过程如图3所示。
图3(a)中,OA为采坑边坡,采坑边坡坡降为Jm;OB为侵蚀临界,即冲沟达到溯源侵蚀平衡比降Jc时的最大冲刷长度Lm,其水平投影长度为Lmx;OC为任意冲刷沟床面,比降Ji;AB为洪积扇原始坡面,原始坡面坡降为Jo;坡肩A点坐标设为(la,ho);B点为溯源侵蚀尖灭点。
y=Jix
(1)
式(1)中:y为溯源侵蚀沟床任意一点与采坑底部的垂直距离,m;x为溯源侵蚀沟床任意一点与采坑边坡坡脚的水平距离,m;Ji为沟床冲刷比降,Ji∈(Jc,Jm)。
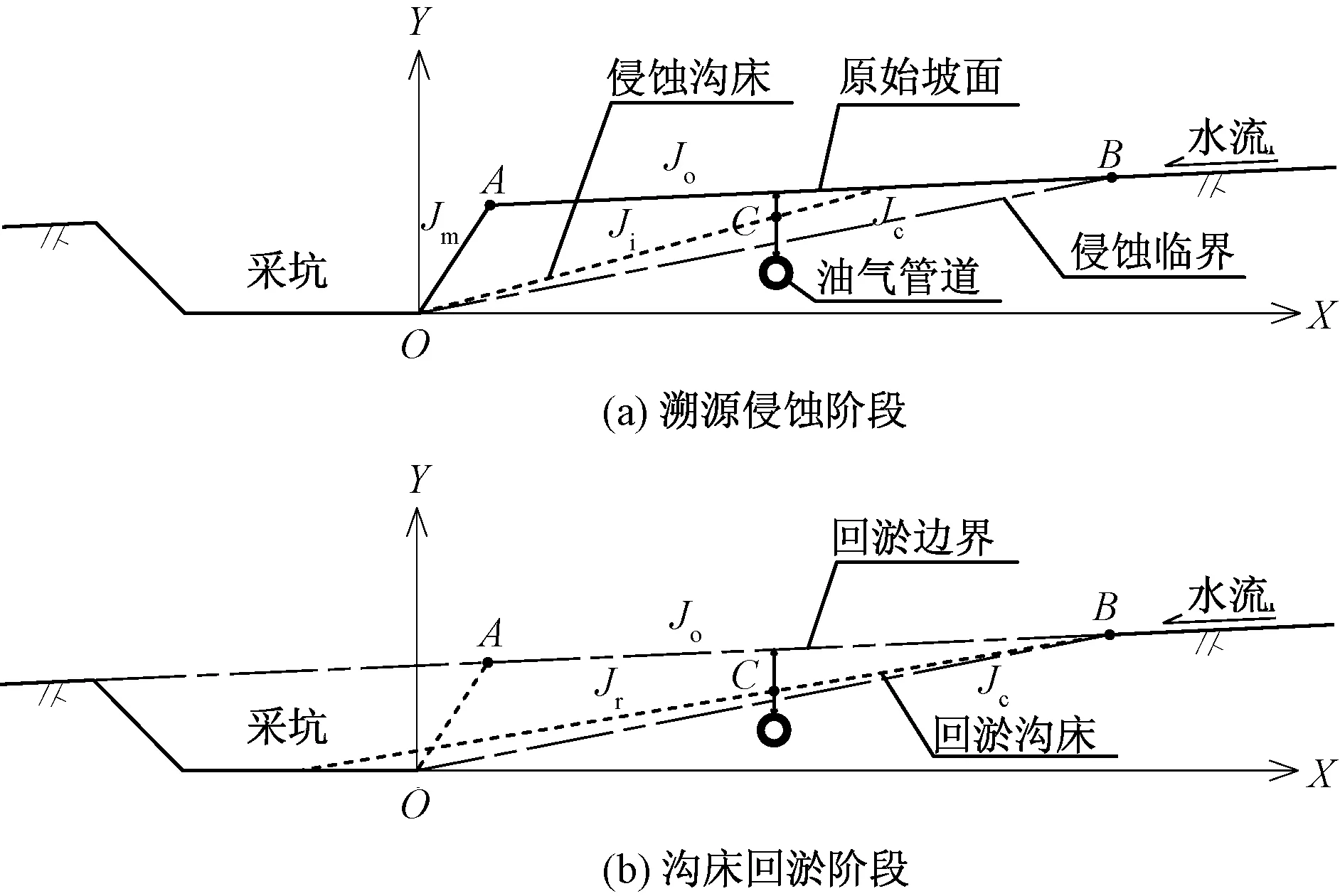
A点为坡肩;B点为溯源侵蚀尖灭点;C点为油气管道在侵蚀沟床 或回淤沟床的地面投影;Jm为采坑边坡坡降;Jo为原始坡面坡降; Jc为溯源侵蚀平衡比降;Ji为沟床冲刷比降;Jr为沟床回淤比降图3 采坑区冲沟演变过程Fig.3 Evolution process of gully in sand pit area
图3(b)中,BA为回淤边界,其极限回淤比降等于原始坡面坡降Jo;BC为任意回淤沟床面;Jr为沟床回淤比降,Jr∈(Jo,Jc)。
y=a+Jrx
(2)
式(2)中:a为冲沟沟口(采坑边坡坡脚)沉积层厚度,m。
2.2 采坑区管道埋深预测模型构建
依据《油气输送管道穿越工程设计规范》(GB 50423—2013),洪积扇管道埋深计算公式为
Hi=Hs-hi
(3)
式(3)中:Hi为管道埋深,m;Hs为管道设计埋深,m;hi为管道覆土层冲刷深度,m。
依据图3(a),由式(1)推导得出溯源侵蚀阶段管道覆土层冲刷深度hi计算公式为
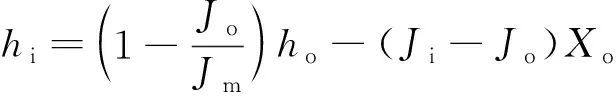
(4)
式(4)中:ho为采坑深度,m;Xo为管道与采坑边坡坡脚的水平距离,m。
依据图3(b),由式(2)推导得出沟床回淤阶段管道覆土层冲刷深度hi计算公式为

(5)
将式(4)、式(8)代入式(3)得出管道埋深预测模型为

(6)
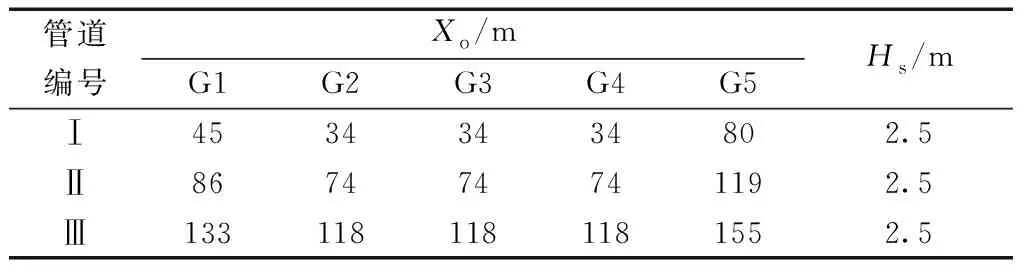
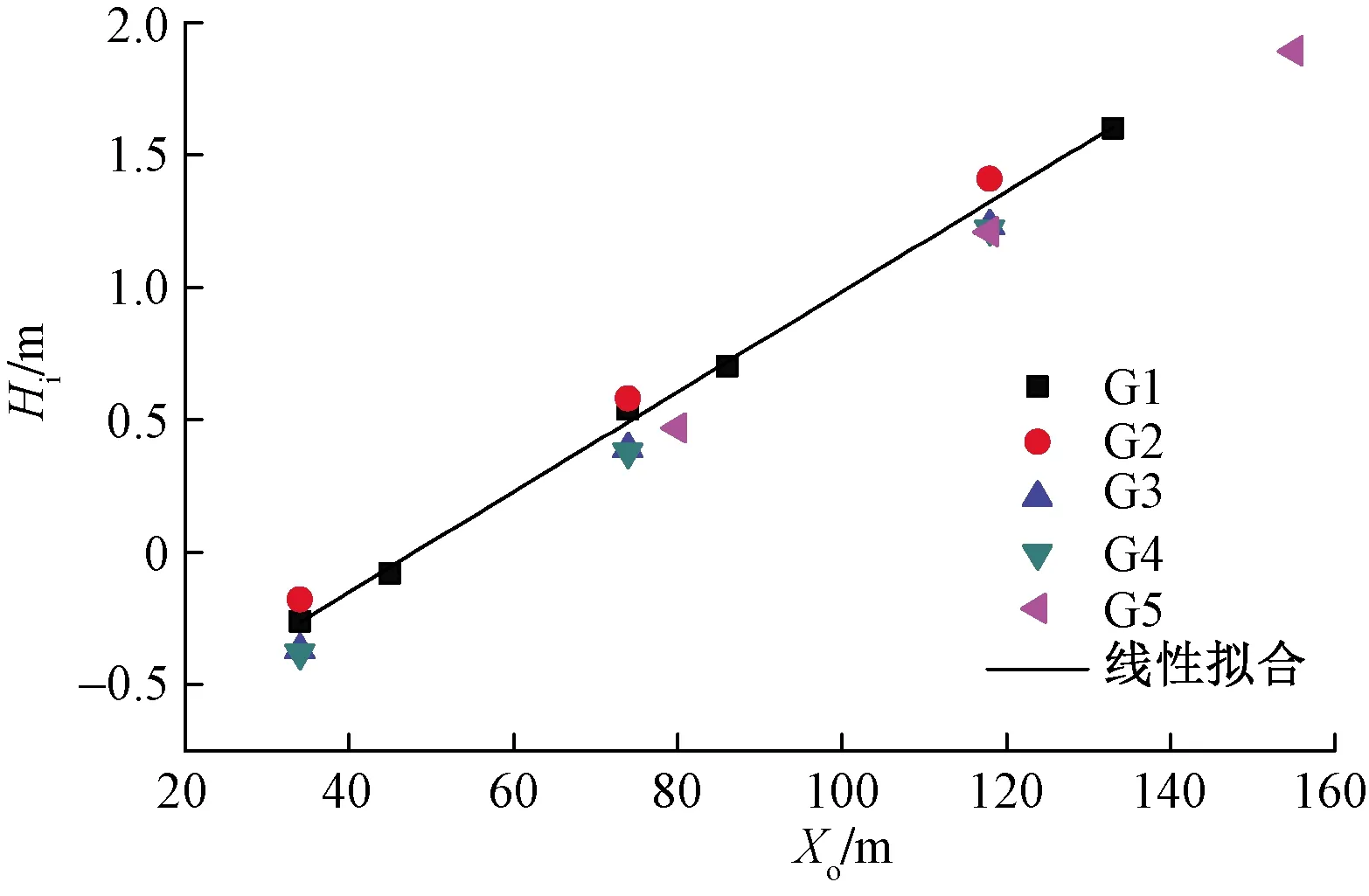
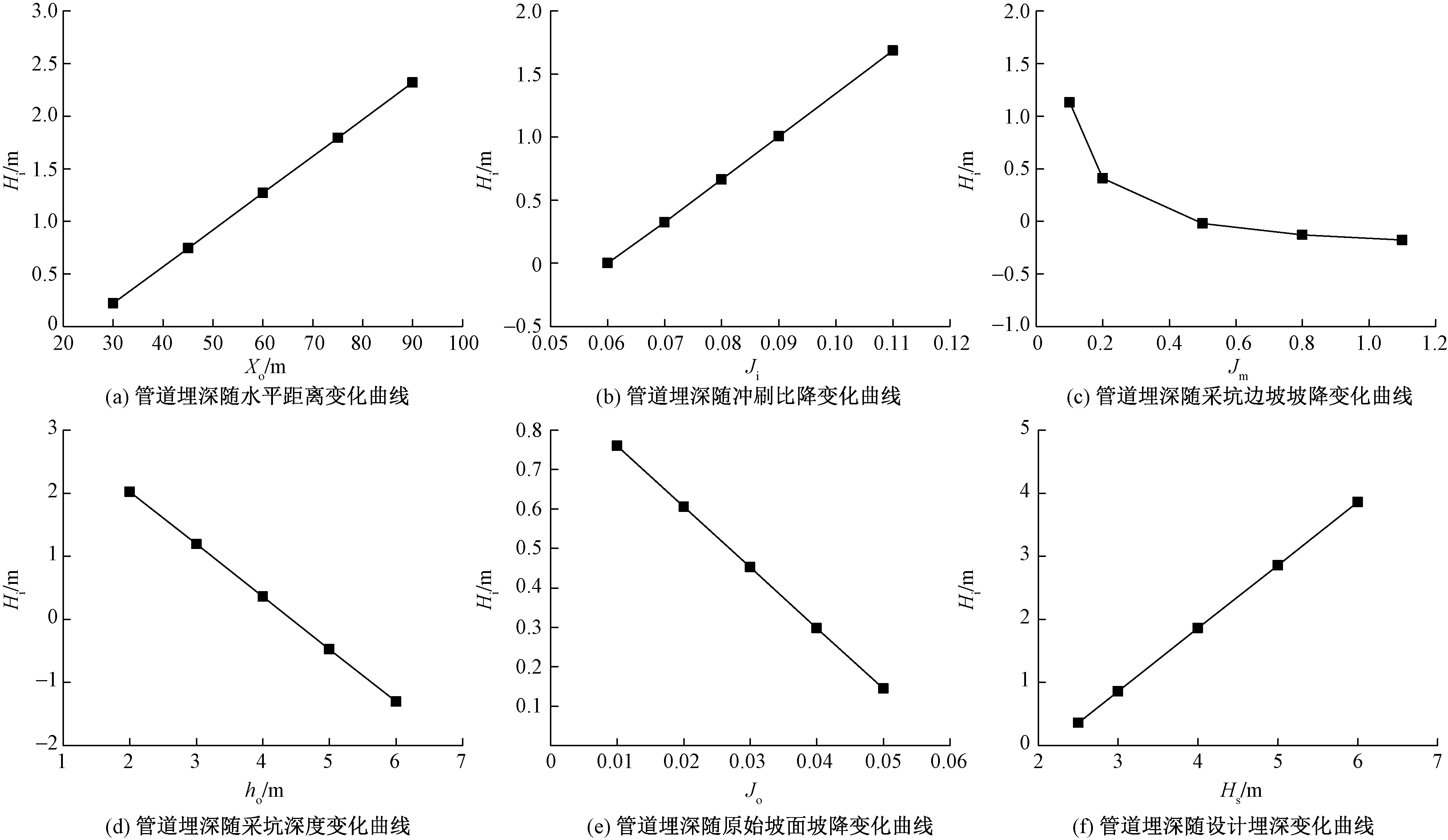
式(6)管道埋深预测结果中,当Hi<0,管道出露或悬空;0≤Hi<1,管道埋深严重不足;1≤Hi 依据图3(a)、式(4),推导得出溯源侵蚀冲刷长度Lmi,其计算公式为 (7) 由此,冲沟达到溯源侵蚀平衡比降Jc时的最大冲刷长度Lm及其水平投影长度Lmx计算公式分别为 (8) (9) 因冲沟平衡比降Jc较小,故Lmx与Lm值接近。 模型参数Jo、Jm、ho、Ji、Jr、Xo及冲沟实际长度l均可通过测量获得,a通过探坑揭露地层获得;Hs为管道设计埋深,即非冲沟发育区域实际埋深,可通过雷迪探测获得,结果如表1、表2所示。 表1 研究区模型参数值 表2 管道与冲沟沟口的水平距离 研究表明溯源侵蚀平衡比降Jc与冲刷流量、冲刷时间、沟床颗粒粒径、糙率、原始坡降等有关,且通过经验公式计算很难准确获得[17-19]。鉴于此,因采坑区G1冲沟历经多年多次间歇式溯源侵蚀,目前处于回淤阶段,假设其沟床冲刷在过去某一时刻已经达到侵蚀临界。通过实地考察与探坑开挖,找到G1冲沟松散新近沉积层与原地层的界限,即侵蚀临界。沟床高程E自原始坡面下降至侵蚀临界,然后又上升至回淤沟床,其演变过程可认定为已经由溯源侵蚀阶段进入了沟床回淤阶段,如图4所示。 图4 G1沟床高程变化曲线Fig.4 Change curves of G1 gully bed elevation 图4中,在溯源侵蚀阶段,随着沟脑持续发育,其冲刷长度Lmi逐渐增加,直至最大冲刷长度Lm;冲刷深度hi相应增加,其深度自下游至上游依次减少;冲刷比降Ji逐渐增大,沟床无限接近侵蚀临界。在沟床回淤阶段,自侵蚀临界起,回淤比降Jr持续降低,将无限接近原始坡面坡降Jo;沉积厚度a逐渐增加,且下游厚度大于上游。 在侵蚀临界,冲刷比降Ji、回淤比降Jr与平衡比降Jc相等。依据G1冲沟侵蚀临界沟床拟合公式E=0.055Lmi+1 837(R2=0.98),得到采坑区冲沟溯源侵蚀平衡比降Jc值为0.055,其中E为沟床高程。 3.3.1 管道埋深预测结果验证 将表1、表2参数代入式(6),计算得到管道Ⅰ~Ⅲ与G1~G5冲沟15处穿越点的预测埋深Hi,其与实测值对比结果如表3所示。 表3 管道埋深预测值与实测值对比 G2~G4冲沟处于溯源侵蚀阶段,管道Ⅰ埋深预测值小于实测值,偏差范围为34%~69%,偏差均值为52%;管道Ⅱ埋深预测值趋近实测值,偏差范围为5%~9%,偏差均值为7%;管道Ⅲ埋深预测值大于实测值,偏差范围为4%~7%,偏差均值为6%。对比得到,管道Ⅰ埋深预测结果偏差较大。现场调查发现,G2沟床15、24、32 m依次发育跌水陡坎3处,均深0.4 m;G3沟床17、27 m依次发育跌水陡坎2处,分别深1.1、0.5 m;G4沟床17、25 m依次发育跌水陡坎2处,分别深1.8、0.9 m。跌水陡坎引起G2~G4中、下游沟床局部冲切,不仅影响冲沟的整体发育,而且导致上游沟床较为平顺,切深普遍较浅。管道Ⅰ位于G2~G4沟床跌水陡坎上游,水平距离2~9 m,致使其埋深预测值与实测值偏差较大。管道Ⅱ距离跌水陡坎42~49 m,管道Ⅲ距离跌水陡坎86~93 m,其埋深预测值与实测值偏差随着水平距离的增加而减小。 G1与G5冲沟处于沟床回淤阶段,管道Ⅰ、管道Ⅱ埋深预测值趋近实测值,偏差范围依次为13%~23%、4%~13%,偏差均值依次为18%、9%;管道Ⅲ埋深预测值接近实测值,偏差范围2%~5%,偏差均值4%;埋深预测值与实测值偏差自管道Ⅰ至管道Ⅲ依次降低。 综上,15处水毁点管道埋深预测值与实测值偏差小于15%的比例达73%,偏差小于10%的比例达60%,预测结果基本可信;随着管道与采坑距离的增加,其埋深预测值与实测值依次增大,二者偏差依次减小;回淤阶段预测值与实测值偏差整体上小于溯源侵蚀阶段;相比实测值,模型预测值更趋于保守。 3.3.2 溯源侵蚀冲刷长度验证 利用式(7)计算得到G2~G4冲刷长度Lmi,式(8)计算得到G1~G5达到溯源侵蚀平衡比降0.055时的最大冲刷长度Lm,与冲沟实际长度l的对比结果如图5所示。 图5 冲刷长度预测值与实际沟长对比Fig.5 Comparison of predicted scour length with actual gully length 图5中,研究区G1~G5达到溯源侵蚀平衡比降0.055时的最大冲刷长度接近,且均影响Ⅰ~Ⅲ 3条管道。G1和G5最大冲刷长度Lm预测值小于实际沟长l,偏差6%~9%;G2~G4冲刷长度Lmi预测值大于实际沟长l,其中G2偏差9%,G3、G4偏差接近50%。对比得到,G1、G2与G5预测结果接近实际情况,G3、G4预测结果与实际情况偏差较大。G2沟床发育3级跌水陡坎,均深仅0.4 m,且分布较为分散,对冲沟发育长度的影响较小。相比G2,G3与G4沟床虽发育2级跌水陡坎,但均深1.1 m,最大深1.8 m,且分布较为集中,其在一定程度上减缓了冲沟发育速率,并影响其长度,导致预测值大于实测值,且偏差较大。 3.3.3 管道最小埋深预测 管道穿越溯源侵蚀冲沟区域最小埋深关乎其运营安全,故进行最小埋深预测意义重大。依据表1、表2的参数,利用式(6)计算得到G1~G5冲沟达到溯源侵蚀平衡比降0.055时的管道埋深Hi,该埋深为管道运营期间可能出现的最小埋深预测值,结果如表4所示。 由表4可知,管道Ⅰ距离采坑边缘34~80 m,最小埋深预测范围-0.38~0.47 m,差值0.85 m;管道Ⅱ距离采坑边缘74~119 m,预测最小埋深范围0.38~1.21 m,差值0.83 m;管道Ⅲ距离采坑边缘118~155 m,预测最小埋深范围1.22~1.89 m,差值0.67 m。其中,G1、G5冲沟预测结果与现场实际情况基本吻合,G2~G4冲沟预测结果有待实践检验。受天然采坑边界不规则影响,同条管道与采坑边缘距离的不同导致最小埋深预测值具有较大差异性,因此,管道状态应依据最小埋深预测值进行分段评价。 表4 管道最小埋深预测结果 管道最小埋深Hi随着水平距离Xo的增加而增大,二者呈线性正相关,拟合公式Hi=0.02Xo-0.94(R2=0.99),如图6所示。 图6 管道最小埋深预测值曲线Fig.6 Prediction curve of minimum buried depth of pipeline 研究区,在采坑均深4 m,原始坡面坡降0.036、管道设计埋深2.5 m等工况下,距离采坑边缘50 m以内区域,管道最小埋深预测值均小于0,发生露管、悬管的可能性大;距离采坑边缘50~100 m区域,管道最小埋深预测值0~1 m,埋深严重不足;距离采坑边缘100~170 m区域,管道最小埋深预测值1~2.5 m,其埋深虽未达到设计要求,但整体上风险较低;距离采坑边缘170 m以外的区域基本不受溯源侵蚀冲沟的影响。 综上,拟建管道Ⅰ设计埋深应考虑采坑溯源侵蚀冲沟的影响,在役管道Ⅱ应提前布设浅埋防治措施,在役管道Ⅲ维持现状。管道最小埋深Hi随着水平距离Xo的增加而增大,且逐渐趋于设计埋深。 3.4.1 溯源侵蚀阶段 以G2冲沟为例,模型单一参数变化对管道埋深Hi的影响如图7所示。由图7(a)可知,Xo增大意味着管道距离采坑愈远,遭受溯源侵蚀威胁程度愈低,沟床冲刷对管道埋深Hi的影响越小。图7(b)可知,随着冲沟不断发育,比降Ji逐渐减小,管道埋深Hi随之减少。图7(c)可知,采坑边坡坡降Jm增加,管道埋深Hi呈曲线减少,其先陡后缓的变化特征表明缓坡状采坑边坡变化对管道埋深Hi的影响较大,而陡坡状采坑边坡变化对管道埋深Hi的影响较小。采坑深度ho、原始坡面坡降Jo增大,加剧了冲沟发育,管道埋深Hi随之减少,如图7(d)、图7(e)所示。图7(f)可知,管道埋深Hi随着设计埋深Hs增大而增大,由此可见,管道设计埋深从根本上决定了管道实际埋深值及其运营安全状况。 图7 溯源侵蚀阶段模型参数变化对管道埋深的影响Fig.7 Influence of model parameters change on buried depth of pipeline in the stage of retrogressive erosion 综上,在溯源侵蚀阶段,管道埋深Hi与参数Xo、Ji、Hs呈线性正相关,与参数ho、Jo呈线性负相关,与参数Jm呈非线性负相关。 3.4.2 沟床回淤阶段 以G1冲沟为例,模型单一参数变化对管道埋深Hi的影响如图8所示。由图8(a)、图8(c)~图8(e)可知,回淤阶段管道埋深Hi与参数Hs、ho、Jo、Xo的相关性和溯源侵蚀阶段一致。由图8(b)、图8(f)可知,管道埋深Hi随参数Jr与a的增大而增加。另外,管道埋深Hi随着采坑边坡坡降Jm的增大而减少。 图8 沟床回淤阶段模型参数变化对管道埋深的影响Fig.8 Influence of model parameters change on buried depth of pipeline in the stage of gully bed siltation 综上,在沟床回淤阶段,管道埋深Hi与参数Hs、Jr、Xo、a呈线性正相关,与参数ho、Jo、Jm呈负相关。 (1)在季节性洪水冲刷作用下,冲洪积扇区采坑边缘以沟蚀为主,且主要发育于上游侧,其冲沟演变过程包括溯源侵蚀和沟床回淤两个连续的阶段。 (2)管道埋深预测模型避开了冲刷流量、冲刷频次、冲刷时间、地层岩性等不确定性因素的影响,直接从沟床几何形态出发,虽然能快速预测不同冲刷比降或回淤比降下管道埋深,但是受冲沟演变过程假设条件的约束,模型并不能完全模拟现实状况,预测结果与实际存在偏差。模型参数易得,计算简便,适用于冲洪积扇采坑区冲沟演变下管道埋深预测,其结果对管道风险评价、灾害防治、选线等具有一定的参考价值。 (3)溯源侵蚀平衡比降Jc作为冲沟最大冲刷深度、最大冲刷长度的重要计算参数,通过区域历史冲沟调查、测量获取更接近实际情况。Jc除了与冲刷流量、冲刷时间、沟床颗粒粒径、糙率、原始坡面坡降有关外,还与采坑深度密切相关。 (4)溯源侵蚀阶段,管道埋深Hi与参数Xo、Ji、Hs呈线性正相关,与参数ho、Jo、Jm呈负相关;沟床回淤阶段,管道埋深Hi与参数Hs、Jr、Xo、a呈线性正相关,与参数ho、Jo、Jm呈负相关。故拟建管道工程不仅要与采坑边缘保持一定的安全距离,而且设计埋深还需考虑溯源侵蚀冲沟的影响。 (5)溯源侵蚀阶段发育的跌水陡坎在一定程度上减缓了冲沟发育速率,并影响其长度,是导致部分冲沟管道埋深预测值与实测值偏差较大的主要因素。2.3 溯源侵蚀冲刷长度计算
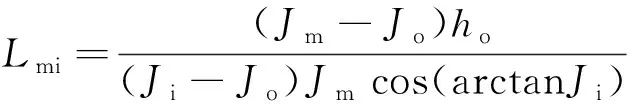

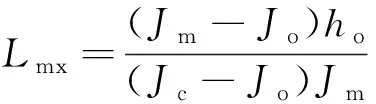
3 模型验证与分析
3.1 模型参数取值

3.2 溯源侵蚀平衡比降Jc

3.3 模型验证与应用



3.4 模型参数影响分析

4 结论

