基于过采样支持向量机的煤与瓦斯突出预测
万 宇, 齐金平, 张 儒, 闫 森
(兰州交通大学机电技术研究所, 兰州 730070)
煤与瓦斯突出是一种影响安全生产的动力灾害[1],形成原因复杂,影响因素众多,突出的发生会造成严重的社会经济损失。基于已发生突出案例的特征参量进行分类研究,有利于利用突出发生与否在指标上的差异化表现准确识别突出,进而对未开采区域的突出危险进行预测,对事故的预控预防具有指导意义。在实际生产中,过去人们常常使用单项指标法、瓦斯地质统计法、DK法对突出进行预测。随着机器学习理论和计算机硬件的发展,基于机器学习的危险预测以其强大的数据分析能力成为学术研究中的热点,如神经网络、深度信念网络、支持向量机(support vector machine, SVM)等在不同预测问题上的表现可圈可点。
付华等[2]提出了一种改进的极限学习机对煤与瓦斯突出强度进行预测;汪莹等[3]构建了基于粗糙集理论(rough set,RS)结合支持向量机(support vector machine,SVM)的煤与瓦斯突出预测模型;顾能华等[4]将核主成分分析(kernel principal component analysis,KPCA)与Takagi-Sugeno(T-S)模糊神经网络结合对突出风险进行预测;邵良杉等[5]将随机森林算法引入突出预测模型解决了数据缺失问题。这些方法的在一定程度上提升的突出预测的精度,但是在最大化全体分类准确率的过程中,容易忽略少数类样本的正确分类,若想训练出优秀的模型需要大量的突出数据,这在实际生产中是很难搜集的。为解决这个问题,引入过采样算法对基于支持向量机的分类预测提供样本支持。
1 支持向量机
1.1 支持向量机原理
支持向量机是一种基于Vapnik-Chervonenkis(VC)维理论和结构风险最小化准则的监督学习算法[6],在面对非线性、小样本问题时表现出色,计算复杂度取决于支持向量的数目,从而避免了“维数灾难”,并且具有良好的鲁棒性和泛化性能。目前已广泛应用于计算机视觉、时间序列预测、人工智能等领域。SVM的基本思想是在特征空间中寻找一个最优超平面,以期两类样本分隔间距最大化。设样本数据集(xi,yi),i=1,2,…,l,x∈Rn,yi∈{-1,+1},其中,l为训练样本总数,n为空间的维数,xi为待分类数据,yi为标记类别,在SVM算法中,满足Mercer条件的核函数K=(xi,xj)可以代替原空间中的内积,也就是将原空间中线性不可分的样本映射到高维空间使其变得线性可分,为了增加对噪声的容错性同时引入松弛变量ξi与惩罚因子C,上述条件可以转化为式(1)带约束条件的优化问题进行求解。
(1)
通过引入拉格朗日对偶定理将上述最优分类问题转化为式(2),决策函数如式(3)所示。
(2)
(3)
式中:w、b分别为超平面的法向量和截距;Φ、L为函数;ξ为松弛变量;αi、αj为拉格朗日乘子。
1.2 支持向量机缺点
以二分类为例,在两类样本数量悬殊的情况下SVM的分类效果会变差,具体失效原因如下。

(4)
(5)

(6)
(7)

(8)
(9)
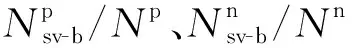
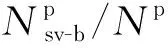
(10)
设经过过采样后的Np=Nn=m,可将式(10)转化为
(11)

2 过采样算法
2.1 BSMOTE算法
Fernandez等[7]提出了合成少数类过采样技术(synthetic minority oversampling technique,SMOTE),与以往简单复制的方法不同,它的核心思想是在少数类样本的连线上随机合成新样本以实现数据均衡,一定程度上解决了分类过拟合问题。王坤等[8]使用SMOTE算法合成气象要素中的少数类样本,再结合逻辑回归模型对短时强降水进行预测取得了较好的效果,但是这种采样使得一些新合成的样本没有提供有效信息且增加了类之间重叠的可能性。Smiti等[9]提出了一种考虑样本分布特点采样的Borderline-SMOTE算法,该算法认为样本越靠近决策边界,其分类意义越高,因此引入k-近邻法(k-nearest neighbor,k-NN)找出边界样本,分别计算少数类样本集中每一个样本的m个近邻样本,近邻样本既可能是同类也可能是异类,如果异类样本数量大于同类,则认为该样本靠近边界,并将其放入一个新集合中以备合成新样本,否则就将该样本点剔除。黄景林等[10]将Borderline-SMOTE算法与卷积神经网络相结合构造了输电线路故障分类模型,提高了对少数类故障样本的识别能力。Borderline-SMOTE算法只对靠近边界的样本进行过采样,使得新合成的样本也处于分类边界附近,保持了正负类边界支持向量的数量一致,根据SVM的原理可知,这对分类器性能的提升是很有帮助的。但是该算法同时也右在3个缺点:①数据呈多簇分布时,合成样本可能会产生新噪声;②如果近邻或参数k值大小设置不当,可能会将位于边界附近的重要样本视作噪声,而k值的大小很难预先确定;③k-NN法不能找到所有的边界点。
2.2 改进的BSMOTE算法
针对第一个缺点,可以将样本点作为一个簇,合并距离最近的两个簇,不断重复直到聚类数为2(少数类和多数类),选出少数类簇,用同样的方法合并最终得到n个簇。

(12)
(13)
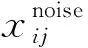
综合二者考虑噪声为真的概率,具体表达式为

(14)
针对③缺点,可以通过考虑样本超平面位置改进合成公式解决,经SVM训练生成超平面可产生图1所示的3种情况:①决策平面轻微偏移,没有错分的正类样本。此时距离超平面越近样本点,越容易为边界点;②决策平面一般偏移,存在部分正类样本错分,对于错分的正类样本点,距离超平面越远的,越容易为边界点,反之,对于正确分类的部分,越近的正类样本点越容易为边界点;③决策平面严重偏移,正类样本全部错分。此时,距离超平面越远的正类样本点越靠近边界。

图1 超平面偏移的3种情况Fig.1 Three cases of hyperplane migration
因此,簇中正类样本信息量的计算公式为
(15)
(16)
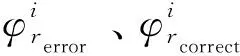
合成新样本的计算公式为

ε′∈{0.5y∈0,1,…,N/k;(1-0.5y∈0,1,…,N/k)}
(17)
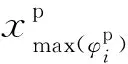
整体的算法流程如图2所示。

图2 改进的Borderline-SMOTE算法流程图Fig.2 Flow chart of improved Borderline-SMOTE algorithm
步骤1 通过聚类分析将少数类样本分成n个簇。
步骤2 在第i∈{1,2,…,n}个簇中,利用k-NN法识别出疑似噪声点,总数记作qi。
步骤3 若没有疑似噪声点,进入步骤5;否则计算疑似噪声点为真的概率。
步骤4 按概率顺序剔除j∈{0,1,…,qi}个噪声点得到簇i′。
步骤5 结合负类样本导入SVM训练,计算正类样本信息量并排序。
步骤6 合成新样本,记为簇i″。
步骤7 训练由簇i″组成的新训练集,计算正确率后返回步骤4直到噪声点全部剔除完,记下准确率最高的簇i″。
步骤8 返回步骤3直到所有簇训练完,将所有的簇i″合并存储。
3 基于过采样SVM的突出预测
3.1 突出机理与样本的采集
由于突出本身的复杂性以及突出发生时采集实时数据困难,使得关于该灾害的机理研究尚未形成一套完整的理论体系,但是经过中外学者们不断地总结经验和模拟实验提出了四类假说:瓦斯主导假说、化学效应假说、地应力主导假说以及目前认同度最高的综合作用假说[11]。
依据综合作用假说,选取垂深、瓦斯含量、煤层厚度、瓦斯压力、坚固性系数5个指标作为影响突出的指标。煤层垂深的大小一方面代表开采地点的应力状况,一般垂深越大,受到地下能量影响破坏内部平衡的可能性越高;另一方面,深部地下土壤环境的密闭性通常高于浅层,这种现象将导致积聚的瓦斯气体不利于挥发而增加突出风险;瓦斯作为形成突出灾害的主要气体,可以在开采过程中通过取样试验初步测量,通常煤层中的瓦斯含量越高,因采掘作业破坏煤层平衡后发生的突出风险也就越高;一定的煤层厚度也是突出发生的必备条件,因煤层渗透性较差,厚煤层的分层会阻止瓦斯逸散,形成瓦斯分层从而增加突出发生可能性;瓦斯压力影响着突出爆发时瓦斯喷出的剧烈程度,因此对确定煤层的突出风险起着至关重要的作用,一般情况下,瓦斯压力越大突出风险程度越高;坚固的煤层由于采掘作业中不易破坏而能够较好地保存吸附的瓦斯气体,通常情况下发生大规模突出风险的概率较小,因此坚固性系数也可作为判断突出风险的指标。
以中国煤与瓦斯突出事故为研究对象,通过整理资料、问卷调查共获得210个样本点,包括50个突出样本,160个非突出样本。从两类样本中分别选取20个作为测试样本,剩下作为训练样本,在此基础上,再将突出样本数逐步缩减至20个、10个共3个训练集,以观察在正类样本数量逐步缩小的情况下算法的表现。具体分布如表1所示,部分数据如表2所示。

表1 实验样本分布情况Table 1 Distribution of experimental samples

表2 部分预测指标集数据Table 2 Partial forecast indicator set data
3.2 预测流程与评价方法
基于过采样算法的SVM预测流程如图3所示。煤与瓦斯突出预测的本质是不平衡数据分类问题,引入混淆矩阵如表3所示。

表3 混淆矩阵Table 3 Confusion matrix

图3 基于过采样算法的SVM预测流程图Fig.3 SVM prediction flow chart based on oversampling algorithm
P/Ne(positive/negative)表示预测对象的所属类别,T/F(true/false)表示分类的正确与否,如TP即将实际有突出的煤矿预测为有突出的样本数量,并选取由此产生的5个指标:敏感性(sensitivity,SEN)、特异性(specificity,SPE)、几何平均值(Geometric mean,G-mean)、F测度(F-measure)、曲线下面积(area under curve,AUC)来评价分类情况的好坏[12],前四者求解公式分别为
SEN=TP/(TP+FN)
(18)
SPE=TN/(TN+FP)
(19)
(20)
PRE=TP/(FP+TP)
(21)
F-measure=2SEN PRE/(SEN+PRE)
(22)
AUC值需要通过计算工作特性曲线(receiver operating characteristic curve,ROC)下面积得到,ROC曲线也称受试者工作特性曲线,其横纵坐标分别是假阳性率(false positive rate,FPR)和真阳性率(true positive rate,TPR),坐标(0,1)对应的是理想的分类模型。曲线越靠近左上角表示分类效果越好,定量指标AUC需要通过积分求面积获得,其大小一般在0.5~1,越靠近1表示越接近理想分类模型。
除上述评价指标外,考虑算法的综合鲁棒性[13],其计算公式为
bm=Rm/max(Ri),i=1,2,…,k′
(23)
式(23)中:bm为算法m的鲁棒性性能,其值越接近1代表相对性能越好;Rm为算法m的调整兰德系数(adjusted rand index,ARI) 值。算法在不同数据集上的整体表现可以通过对bm求和得到。
3.3 算法对比和参数设置
共使用4种算法:SVM、BSMOTE-SVM、SC-SVM、改进的BSMOTE-SVM,对3种不同训练集下预测结果的性能指标进行对比。算法参数尽可能选取最优值,BSMOTE-SVM算法的近邻域参数k在3个训练集中分别选择3、4、4;谱聚类(spectral clustering,SC)保留相同数目的正负类样本;改进的BSMOTE取δ=10-13,α=0.5,k=4;SVM的核函数选择RBF,其中Rδ=10、0.5,C=10,并利用粒子群算法(particle swarm optimization,PSO)对Rδ、C寻优,其中,Rδ为径向基核函数自带的参数,C为惩罚参数,PSO的初始种群与迭代次数分别设为20、100。
3.4 结果分析及对比
利用上述所有方法对煤与瓦斯突出进行分类预测,SEN、SPE、G-mean、F-measure、AUC准确率的结果如表4~表6所示。鲁棒性的结果如图4所示。

表4 不同算法的预测结果比较(Rδ=10)Table 4 Comparison of prediction results of different algorithms(Rδ=10)
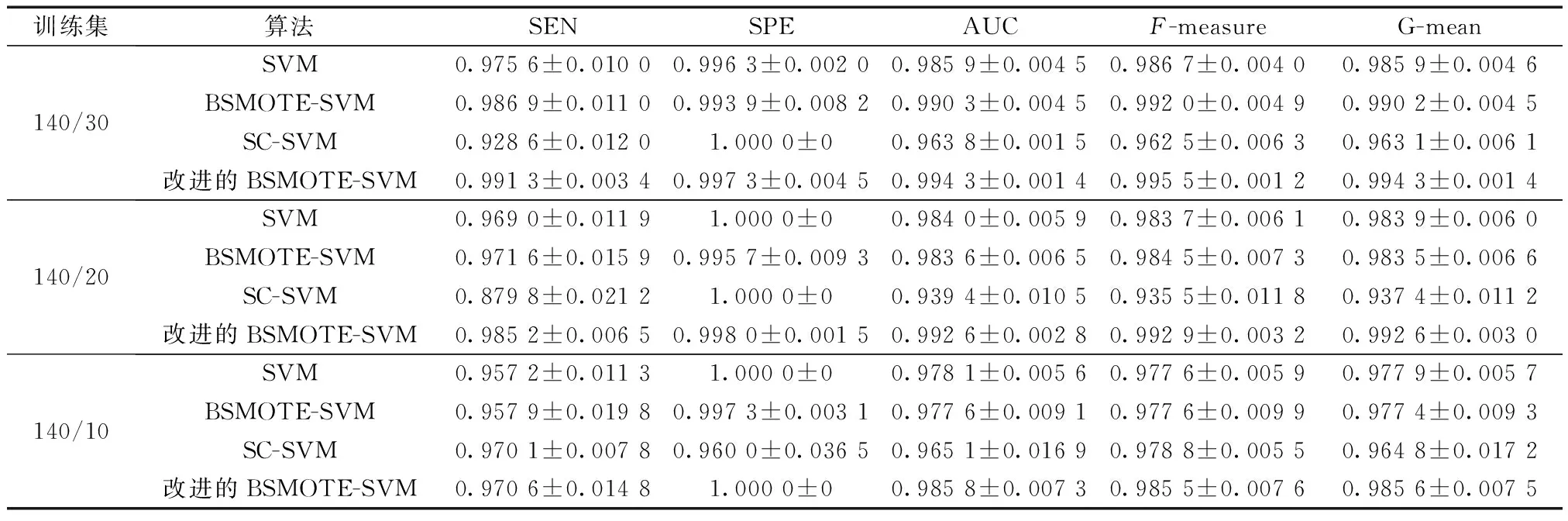
表5 不同算法的预测结果比较(Rδ=0.5)Table 5 Comparison of prediction results of different algorithms(Rδ=0.5)

表6 改进的PSO-BSMOTE-SVM的预测结果Table 6 Prediction results of improved PSO-BSMOTE-SVM

图4 不同算法的鲁棒性比较Fig.4 Robustness comparison of different algorithms
分析表4~表6、图4可知:①过采样算法与支持向量机的组合在G-mean值、AUC值、鲁棒性值上的表现均优于单一支持向量机,说明该组合在煤与瓦斯突出预测领域是适用的,而以SC为例的欠采样算法组合预测效果不如单一支持向量机,推测可能是由于在数据偏少的情况下,欠采样算法删除的样本点包含影响分类决策的重要信息,从而导致决策面发生偏移;②改进的BSMOTE-SVM相比BSMOTE-SVM在分类器性能上有所提升,虽然随着训练集中突出样本的减少,各类算法的性能指标均有不同程度的下降,但是改进的BSMOTE-SVM依然保持了预测结果最优的特点,说明在重采样方面的改进方法是有效的;③不同的Rδ值对应算法的预测效果相差很大,因此对SVM分类器参数Rδ与C进行优化是有必要的。经粒子群算法优化参数后,改进的BSMOTE-SVM算法表现出了更加优秀的性能。
4 结论
依据综合作用假说建立了预测指标集,研究了过采样算法与支持向量机的组合在煤与瓦斯突出危险预测方面的应用。针对BSMOTE算法的缺点作出了相应的改进,通过聚类、去噪、合成新样本为SVM提供样本支持,此外仿真实验还使用了以SC为代表的欠采样算法作为对比,可以看出经过SC重采样的样本集训练后的效果反而有所下降,充分说明了过采样算法在煤与瓦斯突出危险预测领域的优势,针对SVM调参复杂还采用了PSO算法进行参数寻优,取得了非常好的预测效果,在防控灾害上有很好的应用价值。

