一种改进的多分类孪生支持向量机

周开伟 钱雪忠 周世兵

(江南大学物联网工程学院 江苏 无锡 214122)

0 引 言

支持向量机(Support Vector Machine，SVM)是Vapnik等在统计学习理论的基础上提出的一种用于二分类的机器学习算法[1]。该算法在解决小规模样本的分类问题上比一些其他算法有更好的性能，故对SVM的相关研究受到了极大的重视。为了进一步提高SVM的性能，2007年Jayadeva等在广义特征值近似支持向量机的基础上提出了求解二分类问题的孪生支持向量机(Twin Support Vector Machine，TWSVM)[2-3]。TWSVM通过求解一组二次规划(Quadratic Programming Problem，QPP)产生一对非平行的超平面，分别对应于两类相应的样本，使得某一类样本尽可能距离相对应的超平面近，同时尽可能远离另一类的超平面。理论上TWSVM每次求解一个QPP问题的规模是传统SVM问题的一半，所以TWSVM求解问题的速度是SVM的四倍[4]。为了提高TWSVM的性能，国内外众多学者对其进行改进，进而提出了不少改进算法。例如，投影孪生支持向量机(Projection TWSVM)[5]和基于Chen-Harker-Kanzow-Smale(CHKS)函数的光滑孪生支持向量机(CHKS TWSVM)[6]。

现实中，多分类问题是普遍存在的，所以研究多分类具有重要意义。构建多分类支持向量机使用最多的方法是间接构建法，即通过不同的策略将多个二分类器组合成一个多分类器，该方法计算复杂度低，实现简单，且容易理解。目前，已经有许多学者在多分类孪生支持向量机的研究上做出了一定贡献。Xie等[7]结合一对多(one-versus-all，OVA)策略和TWSVM构造出基于一对多策略的多分类孪生支持向量机(OVA-MTWSVM)，该算法将TWSVM运算速度快与OVA策略原理简单且易实现等优点相结合，从而提高了解决多分类问题的效率和速度。Shao等[8]将Knerr提出的一对一(one-versus-all，OVO)策略和TWSVM相结合得到基于一对一策略的多分类孪生支持向量机(OVO-MTWSVM)，此算法因为使用OVO策略，每个子分类器只需两类样本参与训练，训练的速度较快，而且能很好地解决样本不平衡问题。Gu等[9-10]结合TWSVM与图论中的有向无环图(directed acyclic graph，DAG)得到基于有向无环图的多分类孪生支持向量机(DAG-MTWSVM)，该算法与其他策略相比在分类时需要的分类器数量较少，分类速度较快。Yang等[11]将多对一策略(all-versus-one,AVO)与TWSVM相结合得到基于多对一策略的多分类孪生支持向量机(AVO-MTWSVM)，又被称为多生支持向量机(MBSVM)，此算法和OVA-MTWSVM一样具有较低的算法复杂度，因此受到众多学者的关注。除了这四种常用方法外，Xu等[12]将TWSVM与1-versus-1-versus-rest(1-1-R)策略相结合得到一种全新的多分类孪生支持向量机(Twin KSVC)[12]，此算法的每个子分类器既考虑到了待分类的两类样本，同时也将其他类样本考虑在内，具有更好的算法鲁棒性。

本文在多对一的多分类组合策略的基础上提出一种改进的多分类算法。所谓多对一策略就是将训练样本中某一类样本设为负类样本并与设为正类样本的其余所有类样本组合构建多个二分类器。根据测试样本与超平面的距离，若测试样本距离某一类的超平面最远则判定测试样本属于该类。另外，此算法设定每个二分类器的参数都是相同的，以此来解决多分类问题。本文在此基础上通过添加正则项[13]来贯彻SVM的最小结构风险原则[14]，并结合最小二乘思想得到一种改进的最小二乘多分类孪生支持向量机(Improved multiclass least squares TWSVM，IM AVO MLSTSVM)。

1 相关理论

1.1 孪生支持向量机

假设X1∈Rl1×n和X2∈Rl2×n分别表示n维空间Rn中的两类样本，其中X1为+1类样本，样本数为l1，X2为-1类样本，样本数为l2。TWSVM算法主要是在Rn中寻找到以下两个非平行的超平面：

XTW1+b1=0和XTW2+b2=0

(1)

式中：W1和W2是两个超平面的法向量；b1和b2是两个超平面的偏移量。它们是通过求解下面两个QPP得出：

(2)

s.t. -(X2W1+e2b1)+ξ≥e2,ξ≥0

(3)

s.t. (X1W2+e1b2)+η≥e2,η≥0

式中：c1和c2是两个惩罚因子；e1和e2是两个全为1的向量；ξ∈Rl1和η∈Rl2是两个松弛变量。最后决策函数式(4)通过计算测试样本与超平面之间的距离，比较测试样本与各个超平面的距离，与测试样本最近的超平面所对应的那一类为该测试样本所属类别。

(4)

如图1所示，对于两个非平行的超平面，Class1所对应的超平面尽可能与Class1所对应的样本点近而距离Class2所对应的样本尽可能远，同样Class2所对应的超平面距离Class2对应的样本尽可能近，而距离Class1的样本尽可能远。

图1 孪生支持向量机

1.2 基于多对一策略的最小二乘多分类孪生支持向量机

TWSVM最初是为了解决二分类问题而提出来的，但现实中大多数问题为多分类问题，这就需要结合TWSVM和多分类的组合策略构成多分类孪生支持向量机来解决多分类问题。

多对一组合策略是构建多分类器方法最常用方法之一，其原理就是将K类样本中取某一类作为负类，其余K-1类作为正类，构建一个分类器并得到该K-1类样本的超平面，以此类推最后得到K个超平面。AVO策略在每次训练时需要所有的训练样本参与训练，这就需要训练出K个分类器。本文所用算法是基于多对一策略的最小二乘多分类孪生支持向量机(AVO MLSTSVM)[15]，该算法在基于AVO策略的MTWSVM的基础上引入最小二乘思想[16]，用等式约束代替原先QPP问题中的不等式约束，极大地降低了算法求解的复杂性。

基于多对一策略的最小二乘多分类孪生支持向量机(AVO MLSTSVM)算法需要求解以下QPP问题：

(5)

s.t. (XiWi+ei1bi)+ξi=ei1

式中：ci为惩罚因子；ei1∈Rli，ei2∈Rl-li是两个全为1的向量；ξi是松弛变量。式(5)的目标函数的第一项使得超平面尽可能远离第i类样本；第二项为松弛变量，用来最小化来自其他样本点的分类误差。这样使得超平面尽可能远离相应的样本点，而尽可能接近其他样本点。求解式(5)一般使用拉格朗日乘子法[17]，则其对应的拉格朗日函数为：

αi((XiWi+ei1bi)+ξi-ei1)

(6)

根据Karush-Kuhn-Tucker(KKT)条件，分别对Wi、bi、ξi、αi求其梯度并令其为0：

(7)

(8)

(9)

(10)

求解式(7)-式(10)得到分类超平面的法向量Wi和偏移量bi为：

(11)

(12)

最后通过计算测试样本与各个超平面的距离，比较各个距离的大小，与测试样本距离最远的超平面所对应的样本类别为该测试样本所属类。

图2为AVO MLSTSVM在三类样本中的分类示意图，可以看出Plane 1为Class1类样本所对应的超平面，Plane 1尽可能远离Class1样本，并离Class2和Class3样本近，同理Plane 2和Plane 3与Plane 1一样都是距离所对应的样本尽可能远，而距离其他样本尽可能近。

图2 线性AVO MLSTSVM示意图

2 基于多对一策略的改进的最小二乘多分类孪生支持向量机

结构风险最小化原则是通过最大化各类样本之间的边界来实现的。传统多对一策略的最小二乘多分类孪生支持向量机只考虑了经验风险的最小化，却没有将结构风险最小化原则考虑在内。本文在多对一策略的最小二乘多分类孪生支持向量机的基础上引入正则项式[13]来实现最小结构风险原则[14]。

本文对基于一对多策略的改进的最小二乘多分类孪生支持向量机从线性情况与非线性情况分析。在待分类的数据中能够直接找到超平面将待分类的数据分开，称为该情况为线性可分的，即为线性情况。在待分类的数据中无法直接找到相应的超平面将待分类的数据分开，称该情况为非线性情况。这种情况往往通过核函数将待分类的数据映射到高维空间，从而可以解决在低维空间无法直接分类的问题。

2.1 线性情况

假设2维空间R有L个样本，这些训练样本可以被分为K类。其中令Xi表示第i类样本，Yi表示除第i类样本之外其余的样本。那么在线性情况下算法所需要解决的最优化问题可以表示为：

(13)

s.t. (XiWi+ei1bi)+ξi=ei1

式中：Wi是第i类样本的超平面的法向量，bi为偏移量，ci为惩罚因子，ξi为松弛变量，ei1、ei2是两个全为1的向量，θi为添入的正则项式的权重。

用拉格朗日乘子法求解式(13)得：

(14)

最后得到超平面的参数为：

(15)

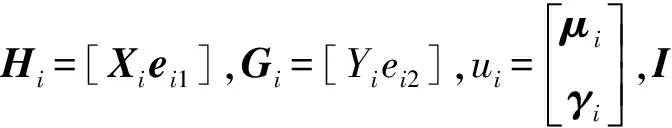
(16)

算法1线性情况下改进的基于多对一策略的最小二乘多分类孪生支持向量机(IM AVO MLSTSVM)的步骤如下：

Step1初始化：训练数据的类数K，Xi为第i类样本，Yi为其他类样本，i为第i类样本的类标。

Step2fori=1:K

(1) 定义两个矩阵Ai和Bi，其中Hi=[Xiei1]，Gi=[Yiei2]。

(2) 选择合适的惩罚因子ci和正则化参数θi。

(3) 根据式(15)确定第i类样本所对应的分类超平面的参数，从而确定第i类样本所对应的超平面。

end

Step3根据式(16)计算测试样本与超平面的距离，测试样本与哪个超平面最远则判断该样本属于哪一类。

2.2 非线性情况

现实情况下大多数需要解决的问题都是非线性的，所使用的算法必须在能解决线性问题的同时也能解决非线性问题。对于非线性的样本需要使用核函数对样本进行处理，首先把样本映射到高维空间中去，然后再利用分类器进行分类。则样本对应的超平面可以表示为：

Ker(Y,DT)μi+γi=0i=1,2,…,K

(17)

式中：D=[XiYi]T，Ker表示选用的适合的核函数。则改进的基于多对一策略的最小二乘多分类孪生支持向量机(IM AVO MLSTSVM)可以表示为：

(18)

s.t. (Ker(Xi,DT)μi+ei1γi)+ξi=ei1

用拉格朗日乘子法求解式(18)：

(19)

求解得到超平面：

(20)

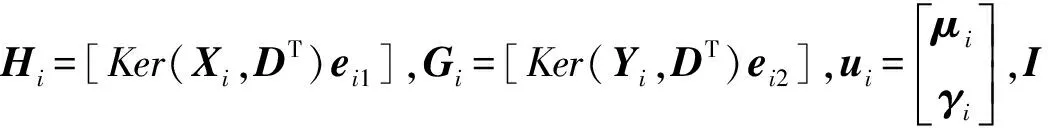
(21)

与线性情况下一样，通过计算测试样本与各个超平面的距离，比较各个距离的大小，测试样本与哪个超平面的距离大，则判定该样本属于该超平面所对应的那一类。

非线性情况下改进的基于多对一策略的最小二乘多分类孪生支持向量机(IM AVO MLSTSVM)步骤如下：

Step1初始化：训练数据的类数K，Xi为第i类样本，Yi为其他类样本，i为第i类样本的类标。

Step2fori=1:K

(1) 定义两个矩阵Hi和Gi，其中Hi=[Ker(Xi,DT)ei1]，Gi=[Ker(Yi,DT)ei2]。

(2) 选择合适的惩罚因子ci和正则化参数θi。

(3) 根据式(20)确定第i类样本所对应的分类超平面的参数，从而确定第i类样本所对应的超平面。

end

Step3根据式(21)计算测试样本与超平面的距离，测试样本与哪个超平面最远则判断该样本属于哪一类。

2.3 复杂度分析

3 实验与结果分析

本节通过实验对本文所提出的算法进行验证。所选用的数据均来自UCI数据库，所有实验均用十次交叉验证。运行环境为4 GB内存，CPU为Intel CORE i3- 4170,3.7 GHz的主频，Windows 10操作系统。所有实验室均在MATLAB R2016a环境上实现。实验所用的数据集具体信息如表1所示。

表1 实验所用数据集信息

在实验设置中，本文选取一对多策略多分类支持向量机(OVA SVM)，多对一策略最小二乘多分类孪生支持向量机(AVO MLSTSVM)和一对多策略最小二乘多分类孪生支持向量机(OVA MLSTWSVM)作为对比实验。并且分别对不同算法选用线性核时算法的表现和选用高斯核时算法的表现作出分析，实验结果均为10次交叉验证所得到的平均精度。实验中对比算法都只有一个惩罚参数c和一个核函数参数σ，本文提出的算法包含三个参数，惩罚参数c、核函数参数σ和一个正则化参数θ,惩罚参数和正则化参数均使用网格搜索选取参数，参数均初始化为之间，同时为了减少运算的复杂度，默认高斯核的核参数σ为2。各种算法在不同数据集上的性能如表2和表3所示。

表2 线性情况下各类算法的分类性能对比(%)

表3 非线性情况下各类算法的分类性能对比(%)

由表2可以看出新提出的算法在使用线性核情况下，在数据集glass、wine、thyroid、cmc和ecoli上面表现的结果较其他三个算法是性能更好。由表3可以得出，IM AVO MLSTSVM算法在非线性情况下使用rbf核函数并且核参数默认为2的情况下在数据glass、wine、thyroid、cmc和ecoli上表现较其他三种算法分类性能更好。由此可看出在大多数情况下提出的算法在较其他三种算法在分类性能上是有改进的。

从表4的分类时间上可以看出本文所提出的算法在线性核情况下时与算法AVO MLSTSVM和OVA MLSTSVM相差较小，同时比OVA SVM的分类时间更好。由表5可以看出在非线性核情况下本文所提出的算法与其他三个算法在数据集glass、wine、thyroid和ecoli上分类时间相差不大，在数据集cmc上与算法AVO MLSTSVM和算法OVA MLSTSVM相差不大，同OVA AVM相比较低。综上所述本文的算法在分类时间上在大多数情况下是有改进的。

表4 线性情况下各类算法的分类时间对比 单位：s

表5 非线性情况下各类算法的分类时间对比 单位：s

本文对比实验采用十次交叉验证，最后结果为十次的平均值，图3-图8为在线性核情况下数据集wine、cmc和ecoli以及在非线性使用RBF核函数的情况下在数据集glass、thyroid和wine上各算法在十次交叉验证中的对比情况。由图3可以看出，本文的算法在线性核情况下在数据集wine上的有着更好的表现，而且总的来说对比其他三种算法都有着更好的表现。由图6可以看出非线性情况下在数据集glass上本文所提出的算法更优于其他三种算法。另外，由图4、图5、图7和图8也可以看出与其他三种算法相比本文算法在分类性能上有较好的改进。

图3 线性情况下各算法在wine上的表现

图4 线性情况下各算法在cmc上的表现

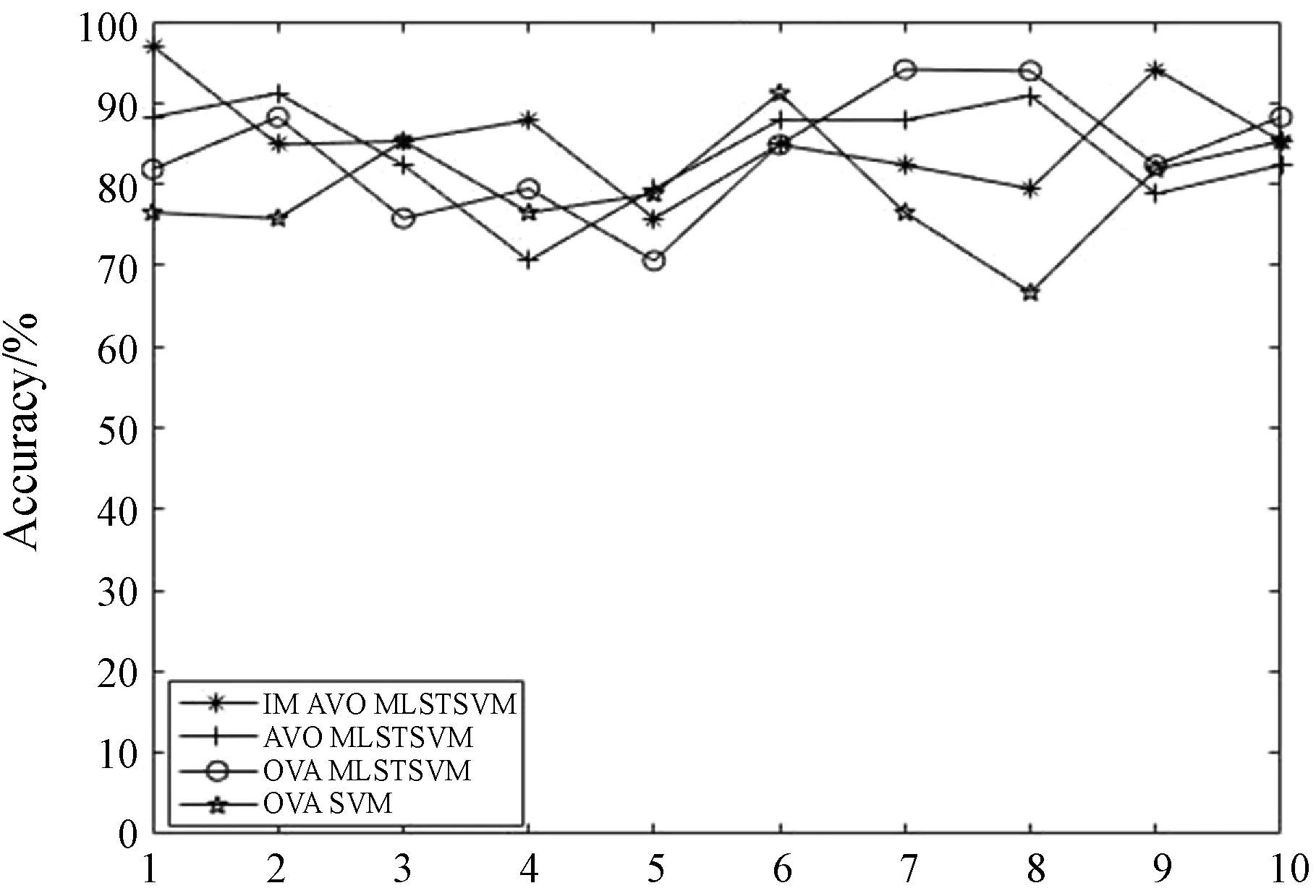
图5 线性情况下各算法在ecoli上的表现

图6 非线性情况下各算法在glass上的表现

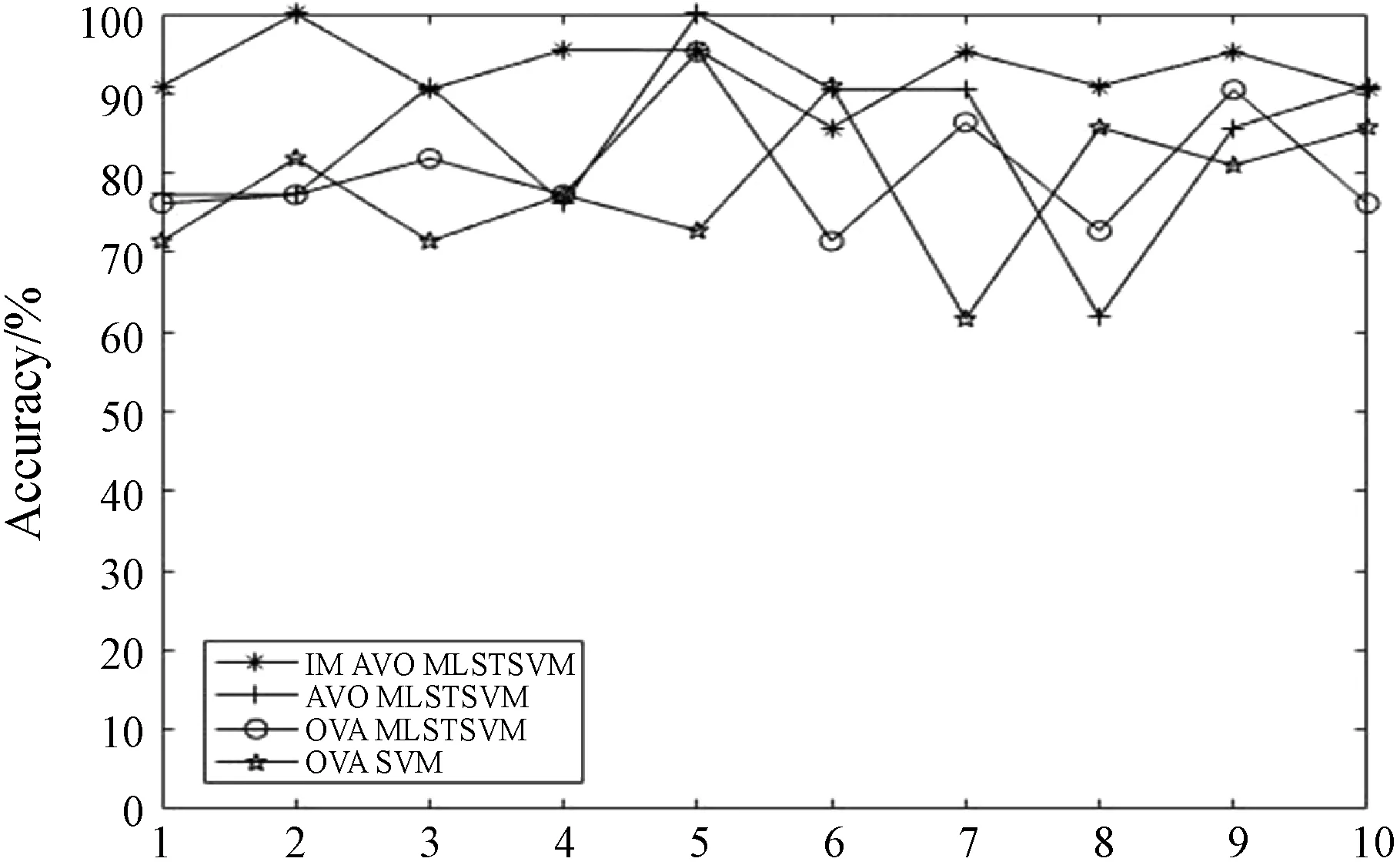
图7 非线性情况下各算法在thyroid上的表现

图8 非线性核情况下各算法在wine上的表现

4 结 语

本文算法是在多对一策略的最小二乘多分类孪生支持向量机的基础上引入正则项式来实现结构风险最小化原则，从而提高分类器的性能。和AVO MLSTSVM类似，本文算法也是将训练数据按照多对一的策略划分。然而AVO MLSTSVM只考虑到算法的经验风险，却没有考虑算法的结构风险。本文提出的算法考虑到算法的经验风险，而且通过引入正则项式来贯彻结构风险最小化原则，能够极大地提高分类算法的性能。通过在UCI数据集上的实验验证，引入的正则化对提高分类器性能是有效的。另外，在面对数据不平衡时，各类样本数相差较大时如何提升算法性能，解决数据不平衡问题还需进一步研究。