基于球谐变换及负荷响应解算地表三维形变

王希禾， 陈 雨， 刘慧玲

(四川大学电子信息学院， 成都 610065)

陆地水储量的大幅度变化会使其周边地表产生相应的形变，严重时甚至会引起滑坡、地震等地质灾害的发生，因此对地表形变的监测及预测是至关重要的课题。由负荷响应理论可知，地表质量载荷的变化会使地球表面产生相应的位移。地球表层大气压力、海洋中的潮汐和非潮汐波动以及陆地上水、雪和冰的分布都是显著的地表质量载荷，其中，对于陆地水储量变化模型的研究较少[1]。

重力卫星技术是研究水储量变化的一项重要技术，自重力恢复与气候试验(gravity recovery and climate experiment，GRACE)重力卫星任务发布以来，吸引了众多中外学者利用其重力场数据进行大地测量及地球物理相关学科的研究[2-6]。Wahr等[7]利用GRACE卫星重力数据获取地球时变重力场信息，并推演出陆地水变化的理论及方法，为后续相关研究奠定了基础。但是使用GRACE卫星数据反演水储量变化的总体趋势时，空间尺度范围在300 km左右，存在信号平滑作用，导致反演精度降低[8-9]。GRACE全球覆盖的特性使其在陆地水储量较少的区域及陆地水较为丰富的区域均可以得到较好的应用，但其产品的球谐系数通常仅有60阶或96阶，丢失了大部分的高阶信息。

相较于GRACE来说，全球导航卫星系统(global navigation satellite system，GNSS)测量的空间分辨率更高，可以通过连续监测站点坐标的变化，反映陆地水和大气等负荷迁移引起的地表形变[10-11]。全球定位系统(global positioning system，GPS)作为GNSS包含的四大导航系统之一，其数据常被用于反演地表质量分布[12-14]。Kusche等[15]对全球GPS形变数据采用了物理激励的正则化方法，保证了更高程度的稳定反演。但GPS系统的安置及运行费用较高，从而限制了GPS网的分布密度，其观测站点的数目通常与地区发展程度成正比，这种现象导致许多地区的水文变化无法监测[16]。

计算负荷地表形变时，相同分辨率情况下负荷格林函数与球谐函数计算结果的精度一致，但在多站点大区域计算时，球谐函数的计算效率比负荷格林函数快100倍左右[17]。现提出一种基于球谐变换解算地表三维形变(垂直形变、东西向形变、南北向形变)及其时间序列的方法，在仅有数字高程模型(digital elevation model，DEM)数据以及水位数据的情况下便可对相应水体负荷造成的地表三维形变进行预测，从而提升全球栅格矩阵的空间分辨率。同时，以三峡水库作为实例进行方法可行性的验证，可将研究方法进一步推广于GPS观测站点稀少或不存在的地区，尤其是地表水文大幅迁移的区域中。例如，正在建设中的埃塞俄比亚文艺复兴大坝，可在已知大坝注水速率的情况下推导其水位变化，继而使用该方法预测地表水储量变化引起的地表三维形变。

1 方法原理

1.1 平均水厚栅格矩阵的建立

通过创建平均水厚栅格矩阵模拟了一个理想化的以水体为质量中心的载荷模型，用于反演水体载荷引起的地表形变。该模型首先创建一个分辨率为0.01°，尺寸为36 000×18 000的空白栅格矩阵。此空白矩阵的横纵坐标分别对应地理坐标系的经纬度，每一栅格长度反映的地理距离约为1.1 km。基于研究区域的DEM数据计算不同水平面以下的蓄水体积和各点水深，并求出研究区域不同水位所对应的水体平均水厚度。在前述创建的空白矩阵中将研究区域水体所对应的各点值设置为平均水厚度值，在此区域外的各点值均设为零，平均水厚栅格矩阵创建完毕。

1.2 球谐变换及负荷形变

将上述创建的平均水厚栅格矩阵扩展为球面谐波，采用了Wahr等[7]于1998年提出的球谐系数表达式，其计算公式为

(1)

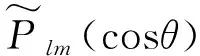
负荷勒夫数被用来表示重力位对负荷引力位的响应，简称负荷数。负荷勒夫数与地球自身内部结构及物质的密度和弹性分布有关，一般表示为k、l、h，可用于表示地球在负荷作用下发生的形态变化[18]。地球表层大气、陆地水以及海洋等负荷的质量发生变化，均会使地球重力场产生相应变化，形成负荷引力位，进而引起地球内部质量的重新分布。反演陆地水储量变化以及地表形变时，由于球谐系数阶次的增加，需要加载对应阶数的负荷勒夫数共同参与计算，一般采用的数据为Farrell[19]于1972年推导的经典解。研究方法采用郭俊义等[20]求解的负荷勒夫数渐进值，该值比Farrell[19]的结论在精度上高出一个数量级。通常以等效水高的形式表示陆地水储量变化，其计算公式为[21]

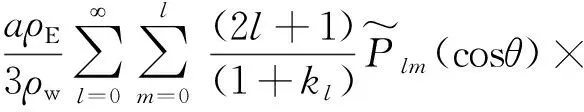
[ΔClmcos(mφ)+ΔSlmsin(mφ)]

(2)

式(2)中：ΔEWH(θ,φ)为等效水高；ρE为固体地球的平均密度，ρE=5 517 kg/m3；kl为l阶处的负荷勒夫数。

地球实质上是一个黏弹体，地表质量载荷发生变化时，会引起相应的地表弹性负荷形变[22]。在展开球谐系数计算地表水文负荷形变时，地表位移与地表质量负荷之间存在一定的关联，两者相关公式为

(3)

(4)

式中：u(θ)为地表垂直方向的位移形变；v(θ)为地表水平方向的位移形变；me为负荷质量；Pl(cosθ)为l阶勒让德函数；hl和ll为第l阶的负荷勒夫数。

利用时变重力场反演地表质量变化以及由此引起的负荷形变时，地表水文负荷导致的形变计算公式为[23]

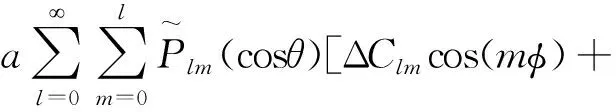
(5)

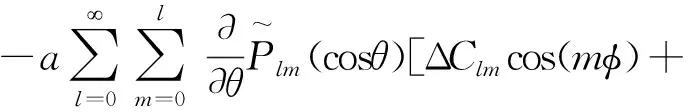
(6)

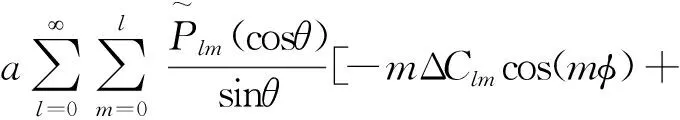
(7)

式中：Δh(θ,φ)为垂直方向位移形变；Δn(θ,φ)、Δe(θ,φ)分别为北向以及东向位移形变，当地壳分别向北、向东移动时，两者为正值，反之为负。

1.3 计算时间序列

利用球谐函数将等效水高及3种地表形变展开之后，得到与平均水厚栅格矩阵同尺寸的栅格数据，并利用该栅格数据求解时间序列。依据Parseval定理可知，在空间域中，信号的平均功率等于其各个谐波分量的平均功率之和。该定理特性的最一般形式也可用于球谐系数的分析中，称为Plancherel定理。利用球谐函数反演变换时，高次谐波的丢失将导致信号在空间域变得平滑和延展。

研究方法的重点不在于每个栅格的值或其平均值，而是以信号变换的总能量为着手点，尽可能减少球谐变换前后能量的损失，得到相对精确的时间序列。Δσ(θ,φ)以及ΔEWH(θ,φ)均表示水高，不同点在于Δσ(θ,φ)表示的质量载荷为平均水厚，在其栅格数据中，只有水库范围内的栅格单元取值为水库的平均水厚度，水库外的其余单元填充值为零；而在ΔEWH(θ,φ)的网格数据中，由于球面谐波被截断造成的延展效应，数值非零的单元分布在远大于水库实际范围的区域中。经实验发现，在研究区域足够广泛的情况下，即信号能量的求和区域增大时，Δσ(θ,φ)与ΔEWH(θ,φ)的平均值更加接近，从而可以由Δσ(θ,φ)变换估算出相对精确的ΔEWH(θ,φ)数值。划定研究区域的范围后，通过对网格数据进行球谐域的变换，结合式(1)以及形变式(5)～式(7)，即可得到由于地表水体变化而引起的地表三维形变时间序列。

2 三峡库区实例验证

2.1 实验区域及数据

为验证研究方法的可靠性，选取三峡水库作为实例验证。如图1所示，三峡水库位于湖北省宜昌市三斗坪境内，库区蓄水工作于2003年开始，正常蓄水情况下库区水位大约保持在145～175 m，总库容量约为393×108m3[24]。三峡工程的建成带来了巨大的防洪效益以及航运效益，水电站的建设更是体现了清洁能源开发的里程碑式发展。

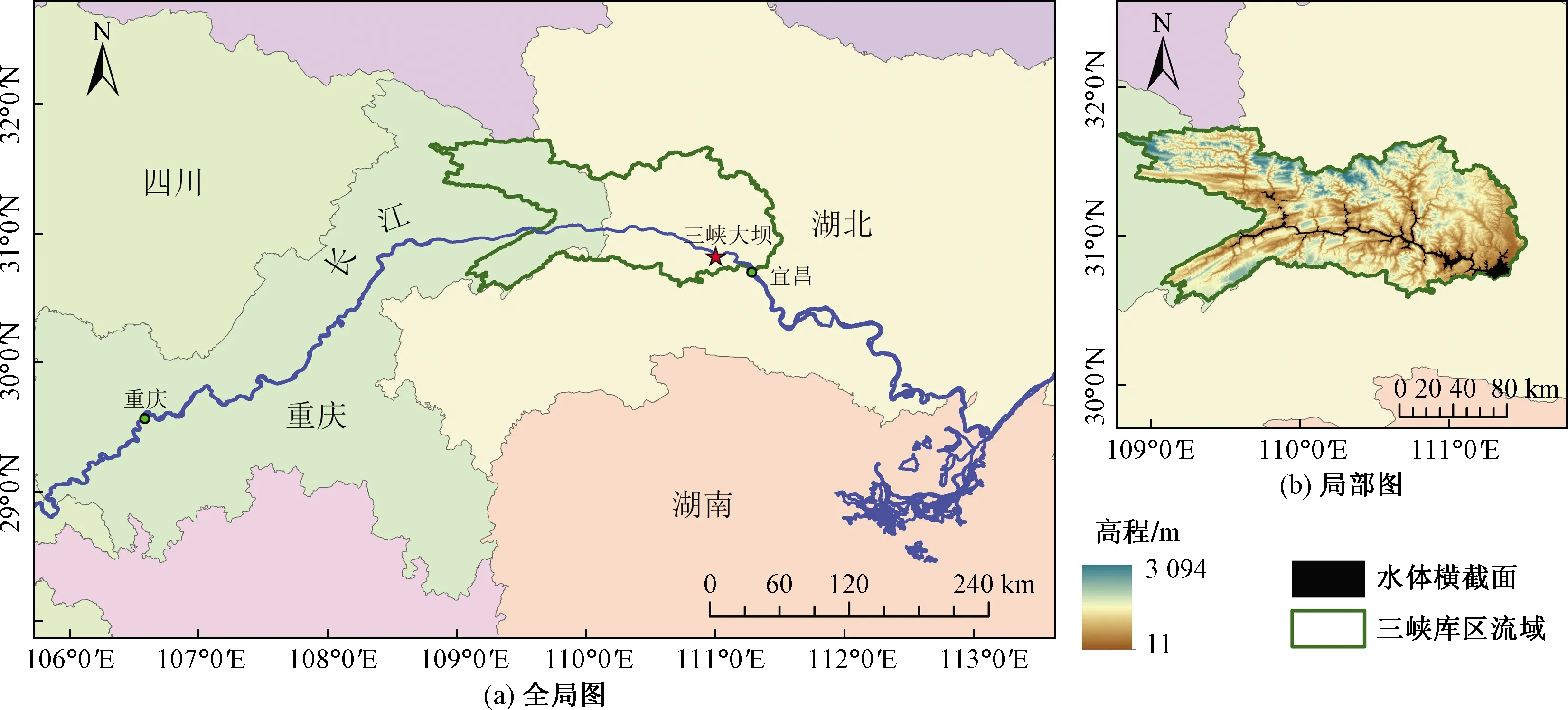
图1 三峡水库位置示意图Fig.1 The location of the Three Gorges Reservoir

使用的数字高程模型数据为NASA提供的SRTM-DEM数据(https://dwtkns.com/srtm30m/)，分辨率为30 m，获取的DEM数据块包含湖北宜昌到重庆的长江主干流。采用的水位数据来源于中国长江三峡集团有限公司(https://www.ctg.com.cn/)发布的水情信息，时间跨度为2011年1月—2018年12月。以2011年1月为基准按月获取，共计96个水位数据。

2.2 等效水高及垂直形变验证

GRACE重力卫星发布的产品在球谐系数上仅有60阶或96阶，缺少中高阶系数包含的细节信息，反映在空间图像中是十分模糊的。利用球谐函数反变换解算等效水高及地表形变时，信号能量主要集中在水库附近，但依旧存在一部分能量向水库边缘不断延伸。当球谐阶数增加时，信号能量会越来越集中，水库位置包含的信息增加，从而使反变换得到的数据更精确。选取球谐截断阶数时，以反演的等效水高与输入的等效水厚度的误差作为判别依据。结果表明，球谐阶数为800阶时，96个数据中，误差率最大为0.815%，最小为0.612%，平均误差为0.742%。由于球谐系数的增加会降低计算效率，且800阶时误差率已经达到较好的期望效果，因此后续计算时间序列时，选取的球谐截断系数均为800阶。

利用式(1)将创建好的平均水厚网格数据扩展至有限次的球面谐波，获取相应的球谐系数，对地表垂直形变进行反演。均以2011年1月为基准，对比计算2018年6月三峡库区发生的地表形变。将球谐系数的截断阶次分别设置为60阶、200阶、600阶、800阶，观测不同系数下垂直形变的空间分布状况。图2中，相较于2011年1月，该月水位高度下降，地壳垂直向上抬升，垂直形变为正值。球谐截断阶数为60阶时，由于信号能量的大量缺失，整个三峡库区范围的形变仅有0.6 mm左右。截断阶数逐渐增加时，高阶系数的能量信息也被计算在内，形变值的“分层”现象越发明显，不同形变值的边界也越发清晰，800阶时三峡库区中心形变值达到6.938 44 mm左右。

图3(a)展示了800阶球谐截断阶数下求得的垂直形变时间序列，每年的1—7月，水库水位持续下降，地壳垂直向上移动，地表垂直形变呈现持续增大的趋势。反之，8—12月份，水库水位不断上升时，地表垂直形变呈减小的趋势。王伟等[25]利用负荷格林函数积分法计算了三峡库区茅坪站水位变化引起的地壳垂直形变，并得出2011年1月—2015年6月的垂直形变时间序列，其观测结果如图3(b)所示。由于该参考文献中茅坪站的水位数据与本文输入的三峡水位数据一致，因此两者结果具备可比性。比较图3(a)、图3(b)中2011年1月—2015年6月的曲线段，可以发现两种方法得到的时间序列变化趋势整体一致，只是在数值上存在差距。参考文献中的地表垂直形变为-1～10 mm，研究方法得到的结果为-0.58～13.53 mm。出现该差距与本文方法采用较高的球谐阶数进行反演有关，球谐系数的增加使解算结果中包含了更多高阶能量信息，水库所在网格区域的累加之和也随之增大、更为精确。

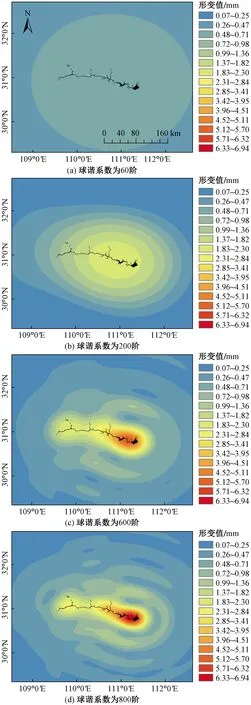
黑色不规则形状为当月水位数据下三峡水库的流域横截面图2 三峡水位变化对地表垂直形变的 影响(2018年6月)Fig.2 The impact of water level changes in the Three Gorges on vertical surface deformation (June 2018)

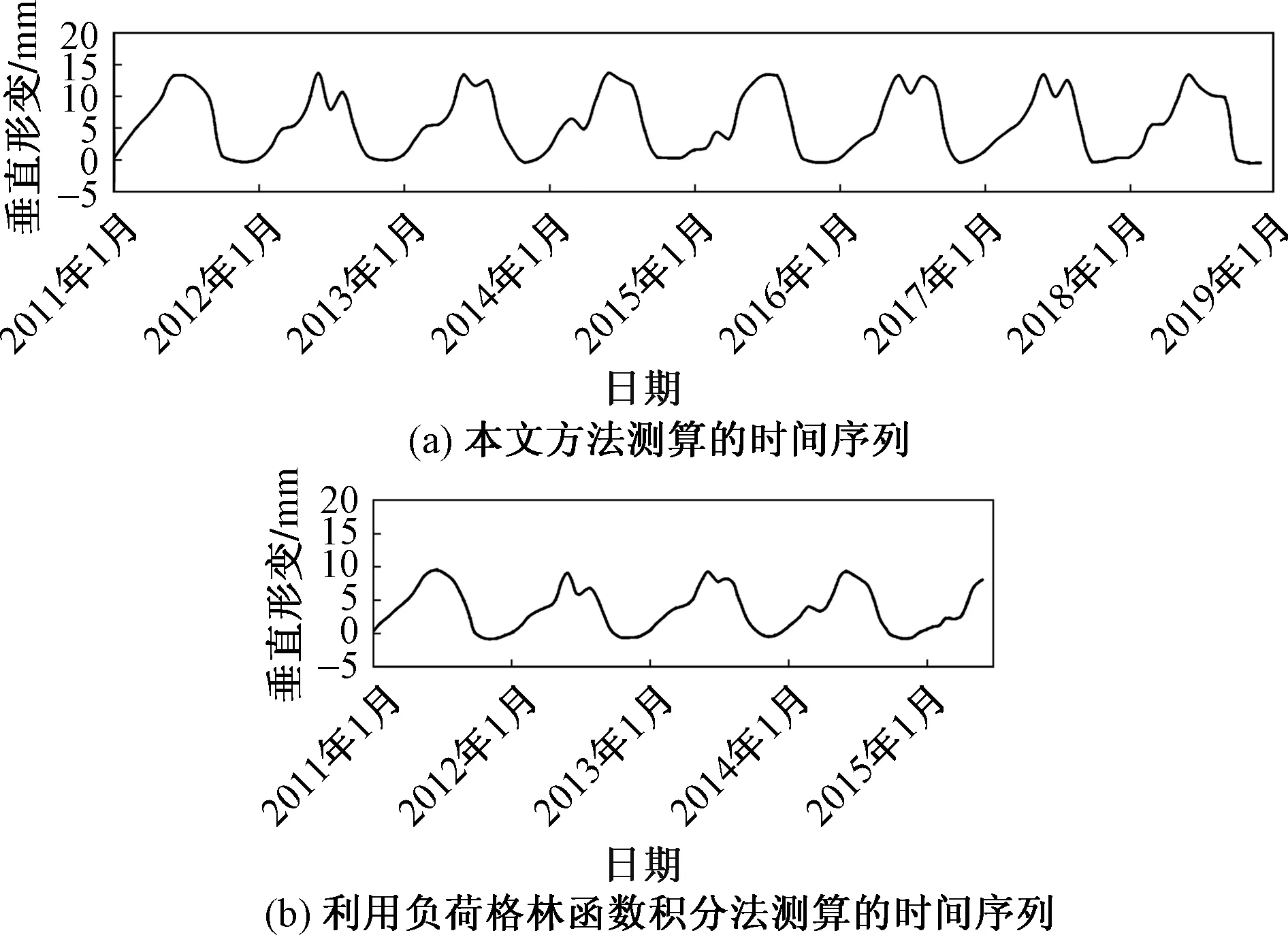
图3 三峡水位变化引起的地表垂直形变时间序列Fig.3 Time series of vertical surface deformation caused by water level changes in the Three Gorges

2.3 解算水平形变及其时间序列

有关三峡地区的水平形变研究相较于垂直形变较少，且多为综合分析，未分解为东向形变及北向形变单独研究，因此研究中只解算水平形变，不做对比。

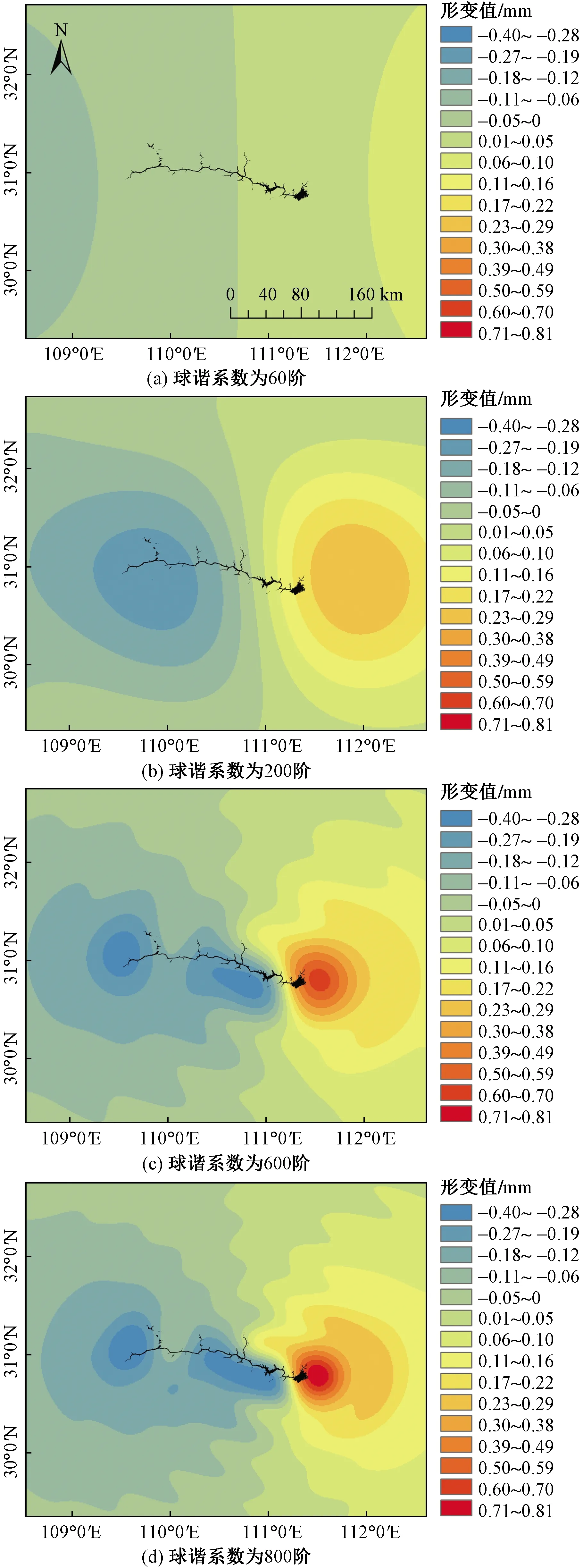
对东向形变进行分析时，依旧以2018年6月的数据为例，图4分别为球谐截断阶数为60阶、200阶、600阶、800阶时计算的东向形变分布图。当球谐截断阶数增加时，计算的东向形变更集中于三峡水库周围，而不是扩散至更远的区域，800阶时库区最大形变达到0.805 566 mm。水位下降时，东侧网格负荷向东移动，位移值为正，西侧网格负荷向西移动，位移值为负；水体负荷均由流域中心向东西两侧移动，地壳沿库区流域向外拉伸。

设置球谐截断系数为800阶时，得到的三峡大坝的东向形变时间序列如图5所示。2011—2018年东向位移的最大绝对差值约为0.77 mm，且每年的形变时间序列都呈先下降后上升的规律性变化趋势，该趋势与三峡水库水位变化趋势大致相同。

黑色不规则形状为当月水位数据下三峡水库的流域横截面图4 三峡水位变化对地表东向形变的影响(2018年6月)Fig.4 The impact of water level changes in the Three Gorges on eastward surface deformation (June 2018)

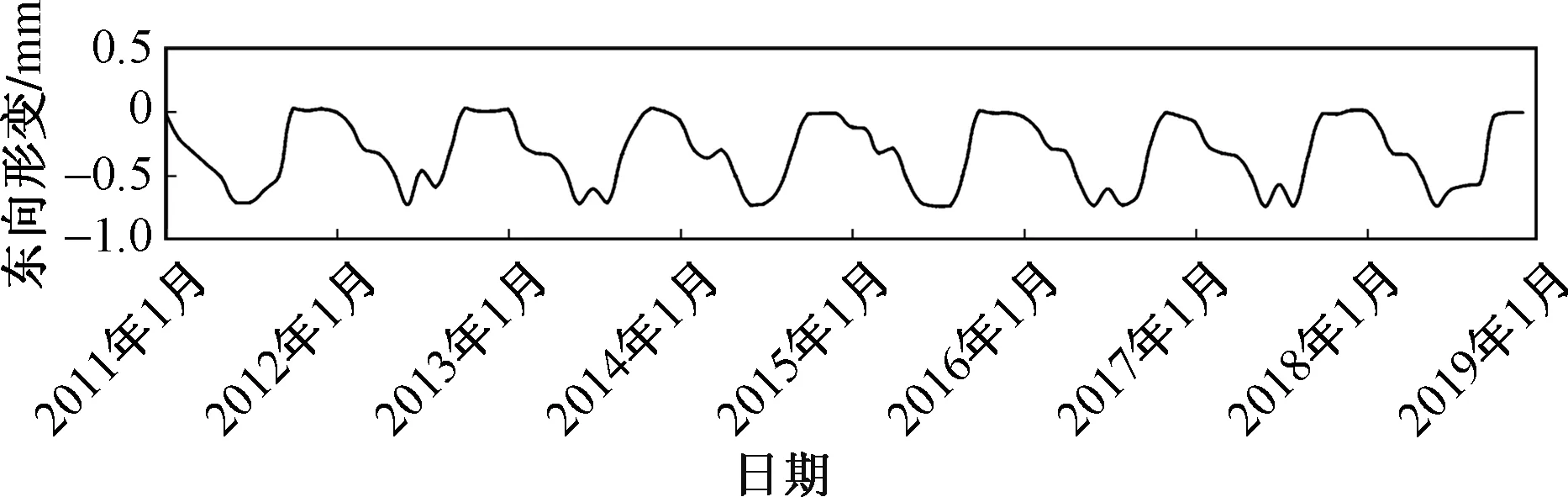
图5 三峡水位变化引起的地表东向形变时间序列Fig.5 Time series of eastward surface deformation caused by water level changes in the Three Gorges

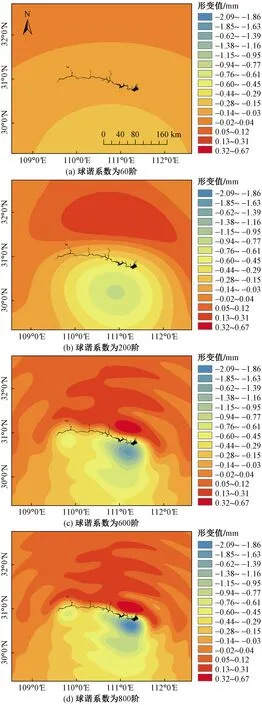
受三峡水位变化的影响产生的北向形变如图6所示，与垂直形变及东向形变相似，随着球谐截断阶数的增加，计算的形变分布图更为精确。概括来说，以三峡水库水体为中心，库区两岸均呈现出由库区中心向外部扩散的趋势。位于库区北部的载荷向北移动，呈现正值，位于南部的载荷向南移动，为负值，且南部位移绝对值略大于北部位移。800阶时，库区北部载荷最大位移值为0.669 066 mm，南部载荷最大位移为2.091 570 mm。

以800阶截断系数计算三峡大坝的北向形变时间序列，得到的结果如图7所示。2011—2018年计算出的北向形变时间序列范围为-1.96～0.07 mm，且该时间序列表现出的年度规律与东向形变时间序列基本相同。

黑色不规则形状为当月水位数据下三峡水库的流域横截面图6 三峡水位变化对地表北向形变的影响(2018年6月)Fig.6 The impact of water level changes in the Three Gorges on northward surface deformation (June 2018)

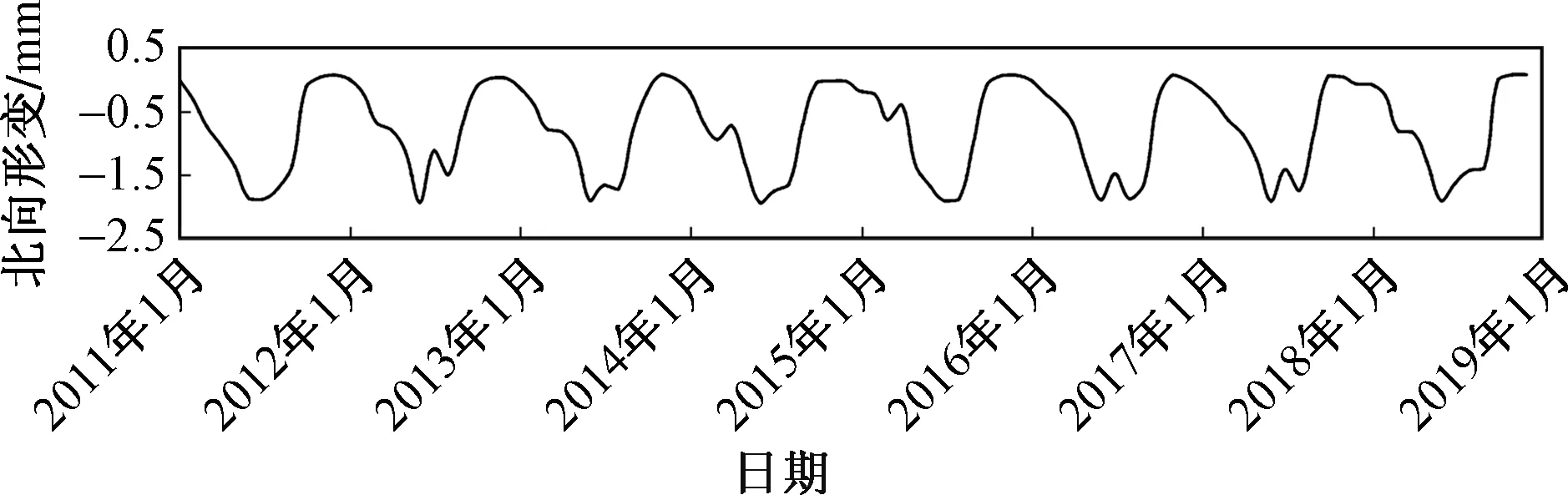
图7 三峡水位变化引起的地表北向形变时间序列Fig.7 Time series of northward surface deformation caused by water level changes in the Three Gorges

3 结论

提出一种利用球谐函数及负荷响应解算地表三维形变的方法，并将反演过程的空间分辨率提高至0.01°。为验证该方法的可行性，使用三峡水库作为实例进行验证，得出如下结论。

(1)首先利用反演的等效水高进行验证，球谐系数为800阶时误差率约为0.742%，即反演精度能达到99.258%。然后计算三峡水库的地表垂直形变时间序列，并与格林函数计算结果对比，二者在趋势上一致，且研究方法由于网格数据精度提高、球谐截断系数增加，使得能量更为集中，计算结果数值较大、更精确。从等效水高以及垂直形变两个角度验证方法可行性之后，依据负荷形变原理计算水平形变，由于以往对三峡地区水平形变的研究较少，且多将北向形变、东向形变综合分析，因此未作对比。

(2)相较于GRACE重力卫星来说，研究方法的局限是在水体负荷变化较为明显的地区中应用时更加有效，如储存大量水体的水库或湖泊，但优点是提高了反演的空间分辨率。此外，假设有一在建水库，GRACE与GPS均不能预测水库蓄水引起的地表形变；但在知晓蓄水速率之后，可以使用该方法，通过对数字高程模型(digital elevation model，DEM)数据处理得到对应水位数据，进而计算出研究区域由水体变化产生的形变数据。因此本方法对于预测及计算一些大型水域地表三维形变的研究来说具有一定的实际意义。