基于动车组接续的高速铁路列车停站方案设计研究

秦永胜，孟学雷，沈发才，张丰婷，刘仁华

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

高速铁路列车停站方案的编制需要考虑各种因素，不仅要满足客流的出行需求，还应考虑实现铁路运输能力的高效利用和运输成本的最小化。近年来，许多学者对这一问题进行了研究，GO‐OSSENS 等[1]通过对几种线路中断模式下的线路规划问题模型进行正确性和等价性证明。为充分体现铁路运输的便捷性，以旅行时间最小为目标构建了停站方案优化模型；CLAESSENS 等[2]通过研究荷兰铁路成本最优分配问题，提出了新的运营成本替代方法，并以此构建了开行方案优化模型，通过将构建的非线性模型转化为具有二元决策变量的线性模型，提出了基于约束满足和分支定界过程的算法，最后以荷兰铁路部分数据进行了实例验证；CHANG 等[3]将旅客的旅行时间和铁路公司的运营总成本综合分析，构建了开行方案优化模型，采用模糊数学规划方法进行求解，最后以台湾拟建高铁的数据进行实例验证；张小炳等[4]通过分析停站方案的均衡性和可达性构建了优化模型，采用遗传退火算法进行求解，并用京沪高铁的数据进行实例验证；牛丰等[5]基于不确定客流，构建了停站方案机会约束规划模型，利用不确定理论的相关知识将其转化为确定性的等价类模型，并通过MATLAB 平台调用GUROBI 优化软件对模型进行求解和计算分析。最后用武广段高速铁路数据进行实例分析；李得伟等[6]以中间站节点服务频率为切入点，构建了带有叉乘约束的非线性规划模型并将其转换为普通的连续性规划问题，进行模拟迭代求解；杨晓等[7]以节点服务频率为约束，构建了列车停站方案优化模型，并使用lingo软件进行模型求解，最后用国内某高速铁路数据进行实例验证；闫海峰等[8]通过考虑运行图的通过能力，以运行线在运行图上占用的时间最少为目标，构建了停站方案优化模型，使用lingo 软件中内置的全局优化算法进行求解，并基于京沪高铁的部分数据进行实例验证；简星等[9]通过推导出发运行线间隔时间公式，以运行线总占用时间最小为目标，构建了停站方案优化模型，采用模拟退火算法进行求解，并以长沙南至衡阳东区段数据进行实例验证；许若曦等[10]以大站间快车比例为切入点，构建了提升旅客出行效率的停站方案优化模型，使用遗传算法进行求解，并基于京广高铁的数据进行实例验证；史峰等[11]以旅客需求为切入点，构造了旅客弹性需求函数，以用户平衡分配为基础，构建了开行方案双层规划模型，并采用模拟退火算法进行求解；史峰等[12]通过综合考虑旅客开行方案和换乘方案，构建了双层优化模型，并采用模拟退火算法进行求解；何宇强等[13]以旅客服务质量为切入点，提出旅客方便度概念；将列车开行最大收益和旅客最大方便度作为目标，构建了多目标双层规划模型，采用混沌算法进行求解，并以石太客运专线数据进行实例验证；周文梁等[14]以铁路运营效益最大和旅客出行费用最小为目标，构建了开行方案和运行图综合优化的双层规划模型，使用模拟退火算法进行模型求解和算例验证；周文梁等[15]基于旅客时段出行需求与广义出行费用建立了弹性需求函数，以列车开行收益最大为目标，构建了基于候选列车集的开行方案优化模型，并使用模拟退火算法进行模型求解和算例验证。综上，目前的文献主要从旅客旅行时间[1,3,5,9,11−12]、出行费用[14−15]、运营成本[2,12]、旅客出行方便度[6−7,13]、运行图通过能力[8−9]等方面对列车停站方案问题展开了研究，构建了线性规划、非线性规划、机会约束规划、双层规划等优化模型，但是对于在列车运行调整计划中考虑停站方案对于动车组数量影响的研究较少。本文从实际出发，在开行区段、客流需求、列车种类、数量、等级已知的条件下，综合考虑停站方案和时间因素对动车组数量的影响，并以此构建了研究模型和设计了求解算法。

1 问题描述

我国现行编制高速铁路列车停站方案时采用的方法大多是根据确定的开行区段、运行径路、列车种类、编组辆数以及客流需求等确定初始的停站方案。从停站方案的编制过程中，不难发现现行的停站方案编制方法没有充分考虑动车组运用的情况。因此，在满足客流需求、通过能力等的条件下，停站方案仍有一定的调整空间使得动车组的运用更合理。

如图1 所示，图中共有4 条运行线，其中运行线G4和G3是接续的，即可以用一组动车组顺序的完成G4，G3 的运输任务；运行线G2 和G1 是不接续的。那么要完成G2 和G1 的运输任务，就需要2组动车组。如果想要减少动车组的使用数量，就必须使得G1和G2接续。一种做法是通过不断地调整运行线的出发时间，使得接续尽可能的多。如图1 中，通过将G2 运行线左移(在满足时间约束的条件下)，使得运行线G2 和G1 接续，从而减少了一组动车组；另一种做法是通过调整运行线的停站方案，如图2所示，通过取消G2运行线的c停站和G1 运行线的b 停站，使得运行线G2 和G1 接续，从而减少了一组动车组。

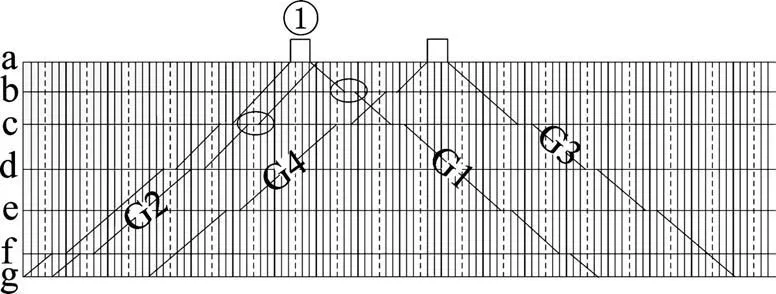
图1 列车运行图Fig.1 Train operation diagram

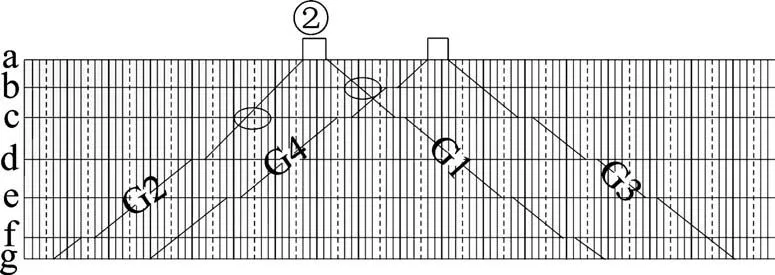
图2 列车运行图Fig.2 Train operation diagram

通过上述举例可以说明：第一，在铺画运行图时，运行线在运行图上的排列方式直接影响运用动车组的数量；第二，在运行线排列方式一定时(运行线始发时间不可调整时)，对于不同的列车停站方案，其停站的次数直接影响着列车运行时间，通过调整车站停站方式，使得小的时间范围内原本不接续的运行线接续(如图2 所示)，从而减少运用动车组的数量。

因此，通过合理地调整列车在中间站的停站方式和运行图中各个运行线的排列方式可以实现旅行时间最小和运用动车组数量最少这一目标。

2 建立模型

2.1 模型假设

1) 选定的客流区段内存在2 种列车种类和等级；

2) 只考虑区间通过能力，不考虑车站通过能力和到发线通过能力的影响；

3) 对初始停站方案的起讫点和运行径路不做改变；

4) 将列车的起停附加时分计入列车的停站时间中，并将停站时间设为定值；

5) 本文旨在研究停站方案对动车组接续的影响，默认在2站间没有可达列车时，旅客选择换乘其他车辆。

2.2 参数列表

参数列表见表1。

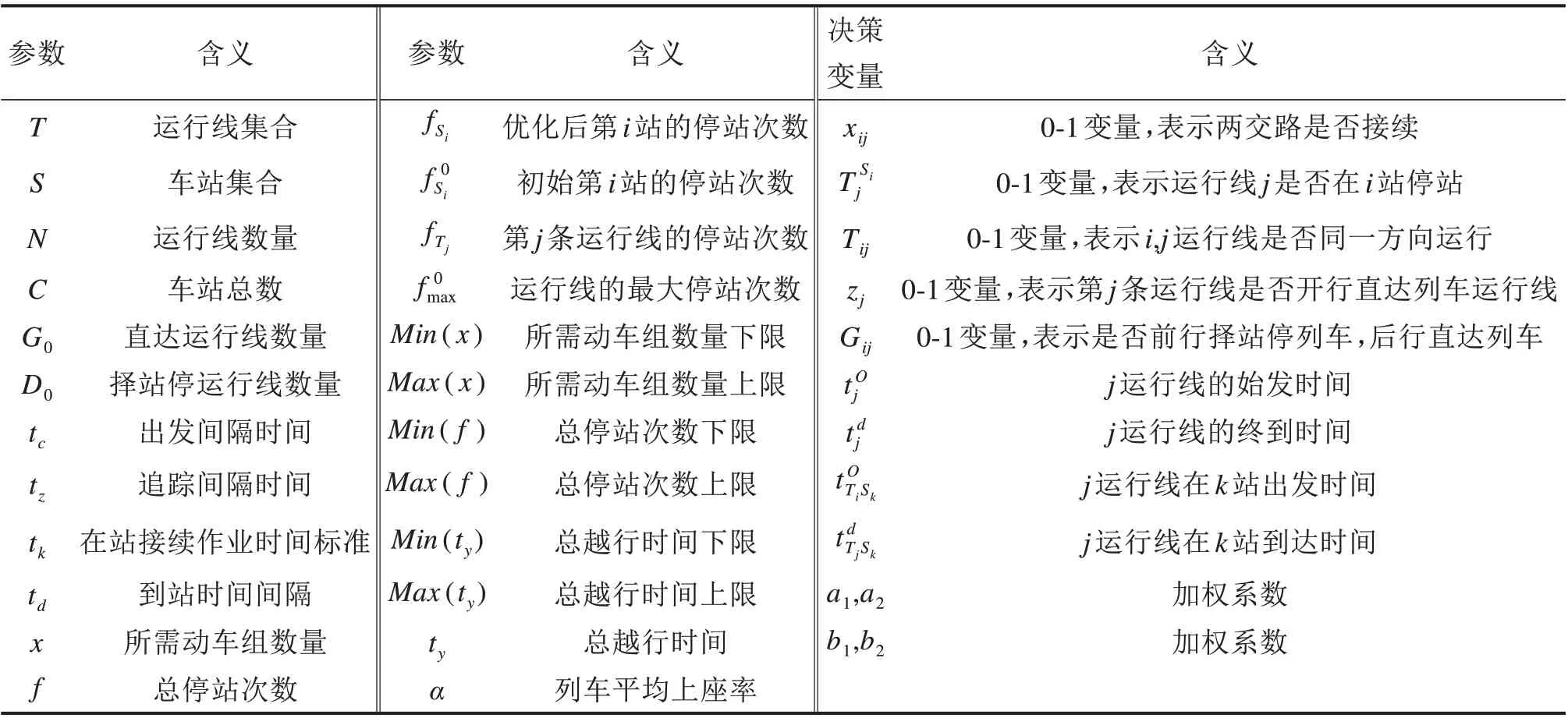
表1 参数列表Table 1 Parameter list

2.3 目标函数

本文所建模型的目标有2个。一是最大程度上减少一日内运用动车组的数量，缓解动车组数量紧张问题。二是最小化旅客旅行时间，提高服务质量。

1) 所需动车组数量：以运行线总数量与接续次数之差表示。

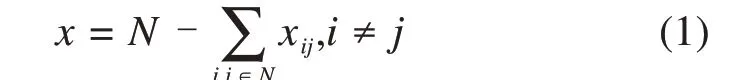
为使各目标量纲统一，进行归一化：

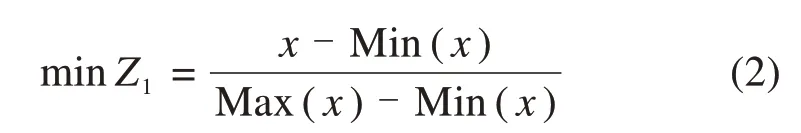
2)旅客旅行时间

对于旅行时间长短的影响因素(不包括线路长度和列车运行速度)主要有2 个：列车停站次数和列车越行时间，尤其是越行时间，其直接增加了旅客旅行时间，影响了旅客的乘车体验。所以将旅行时间最小这一目标转化为不同权重下的停站次数最小和列车越行时间最小，如式(3)～(5)所示。

归一化处理：

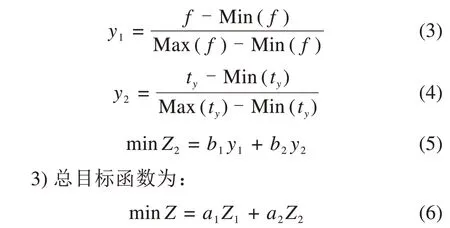
2.4 约束条件

1) 与客户需求有关的约束

旅客服务质量和停站率。本文以各个车站的停站次数来衡量停站方案的旅客服务质量。为不造成运输能力浪费，选取平均上座率α作为初始停站次数的系数，如式(7)所示。

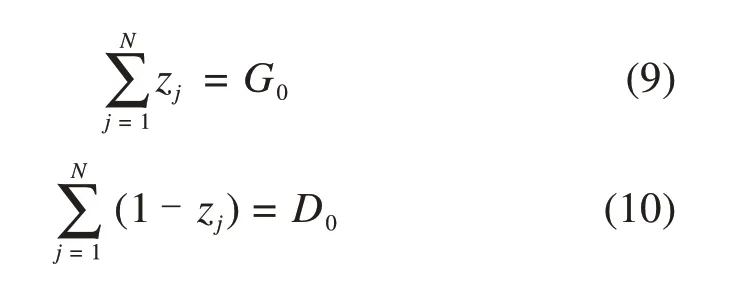
2) 与时间有关的约束

列车出发时间间隔。对于同一方向出发的列车，由于线路采取的闭塞方式不同，就需要采取不同的出发间隔时间，以确保列车运行安全。本文以同方向每个站每列列车与其他列车出发时间之差的绝对值满足出发时间间隔表示，如式(11)所示。

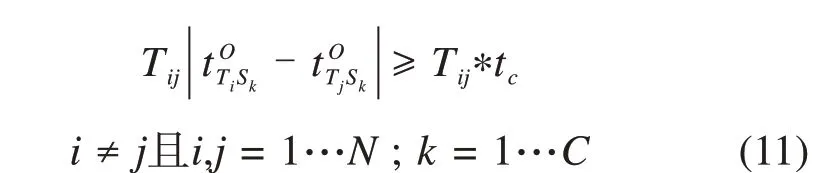
列车追踪时间间隔。对于同向行驶的2 列列车，其必须保持足够的安全距离。在本文中追踪时间间隔主要是确保直达列车与前行择站停列车的安全时距的。为使模型简单，本文以同方向每个站直达列车与择站停列车出发时间之差的绝对值满足追踪时间间隔表示，如式(12)所示。

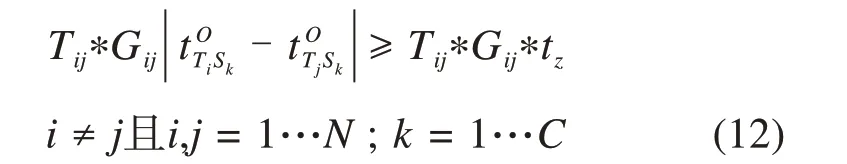
满足在站接续作业时间标准。如果在始发站或终到站2列列车运行线之间存在接续关系，以出发列车出发时间与到达列车到达时间之差满足动车组接续时间表示，如式(13)所示。

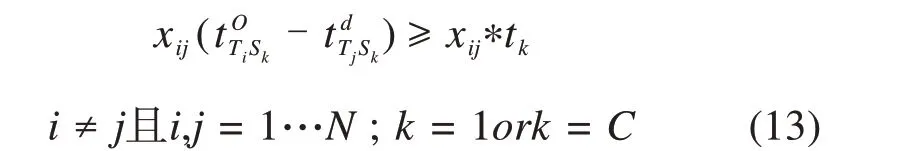
列车到站时间间隔。如果短时间内有大量列车到达车站，会对车站的接车能力造成很大的冲击，而且也存在很大的安全隐患。因此，列车到达时应保持一定的时间间隔。本文以同方向每个站每列列车与其他列车到达时间之差的绝对值满足到达时间间隔表示，如式(14)所示。

3) 与动车组类型有关的约束

在始发站或终到站，如果2条运行线接续，那么这2条运行线所需的动车组类型必须相同。本文以出发运行线所需动车组类型与到达运行线动车组类型相同表示，如式(17)所示。

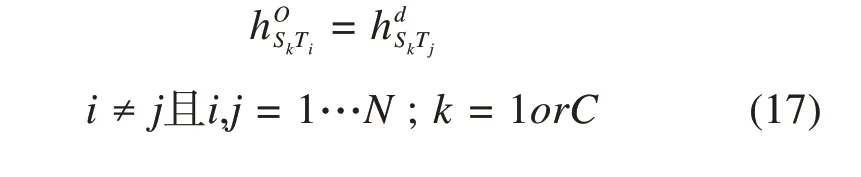
3 求解算法

本文所构建的基于动车组接续的高速铁路列车停站方案设计研究模型，当开行的列车数量和开行区段内的车站数量增加时，模型的变量会大幅度增加，运算规模会呈现几何级数递增。因此本文选取算法复杂程度较低，满意程度较高的人工蜂群随机搜索算法。

3.1 解的向量表现形式

解的信息包括停站方案(fj1)、出发时间(fj2)以及到达时间(fj3)，故解的表达形式为：

因为每条运行线的停站序列是随机产生的，所以每条运行线的停站方案是不同的，即停站方案中的0-1变量构成的停站序列是不同的。

通过决策变量，停站方案fj1以及各站停站时间(包括起停附加时分)可以获得运行线在各站的出发时间和到达时间：

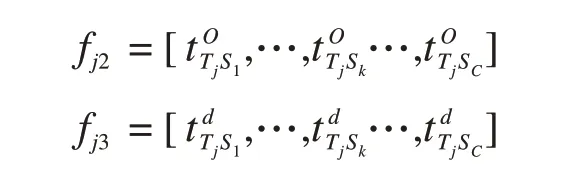
3.2 初始解的生成算法

算法步骤如下。

Step 1：输入原始数据(区间运行时分、各站停站时分、运行线数量(G0、D0)、各站停站频率、各项间隔时间)；

Step 2：根据决策变量生成停站方案；

Step 3：判断停站率等约束，满足，转Step 4；不满足，转Step 2；

Step 4：在可运行时间窗内(即式(15)的可运行时间范围)随机生成直达列车始发时间，并计算在各站出发、到达时间；

Step 5：判断时间间隔等约束，满足，转Step 6；不满足，转Step 4；

Step 6：择站停列车按顺序对第j(j初值为1)条运行线随机生成可运行时间窗内的始发时间；

Step 7：判断是否j%2=1(编写的算法是单数为上行，双数为下行)，是，转Step 8;否，转Step 12；Step 8：计算第k(每次初值为2)个中间站到达、出发时间；

Step 9：判断该站是否被直达列车越行。是，则计算越行时间，并加入停站时间之中；

Step 10：判断时间间隔等约束，满足，转Step11；不满足，转Step6；

Step 11：是否k=C，是，转Step 16；否，k=k+1，转Step 8；

Step 12：计算第k(每次初值为C−1)个中间站到达、出发时间；

Step 13：判断该站是否被直达列车越行。是，则计算越行时间，并加入停站时间之中；

Step 14：判断时间间隔等约束，满足，转Step 15；不满足，转Step 6；

Step 15：是否k=1，是，转Step 16；否，k=k−1，转Step 12；

Step 16：是否j=N，是，转Step 17；否，j=j+1，转Step 6；

Step 17：计算目标值；

Step 18：生成初始解方案。

3.3 算法邻域构造

对于判断邻域解的可行性，在邻域停站方案构造完成后，第一，判断其是否满足客流需求(即式(7)～(8)约束)，不满足则重新构造邻域停站方案；第二，对满足客流需求的邻域停站方案，计算各站(除始发站外)出发到达时间，并判断各时间间隔约束，不满足则重新构造邻域停站方案，构造次数达到邻域内部搜索次数limit1 后，还不能满足时间间隔，则在可运行时间窗内重新生成始发时间，并判断时间间隔约束，直至生成新的可行解。

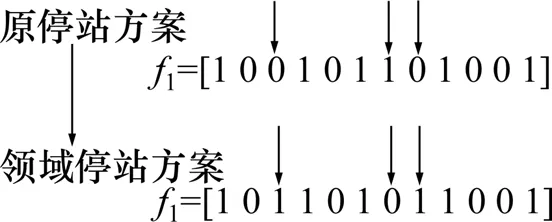
图3 邻域构造示意图Fig.3 Schematic diagram of the domain construction

3.4 算法步骤

Step 1：输入原始数据(车站数量和等级，列车种类、数量和等级，各站停站时间，各站最小停站率，列车最大停站率)；

Step 2：设定算法参数，包括种群规模NP，采蜜蜂数量FoodNumber，局部循环次数limit 和最大迭代次数MaxCycle等；

Step 3：初始化：使用初始解算法生成原始种群解(解的内容包括停站方案、各站出发时间、各站到达时间)；

Step 4：根据目标函数公式计算种群中各蜜蜂(各初始解方案)的适应值，并得出最优初始可行解(即获得最优解H 的停站方案、各站出发时间、各站到达时间、所需动车组数量、总旅行时间)；

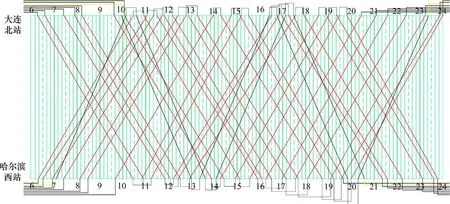
Step 5：采蜜蜂通过邻域构造方法对初始可行解进行优化，若新解FitnessSol

Step 6：根据limit 判断是否有放弃的蜜源，若有，采蜜蜂转换为侦察蜂并随机产生一个新蜜源(即新的可行解)；

Step 7：计算选择蜜源的概率prob；

Step 8：观察蜂根据概率prob 选择可行解，并在该可行解邻域内进行优化，若新解FitnessSol

Step 9：根据limit 判断是否有放弃的蜜源，若有，观察蜂转换为侦察蜂并随机产生一个新蜜源；

Step 10：将当前最优解保存在value，并进行迭代次数检验，iter=iter+1,若iter

Step 11：输出最优解。

4 实例分析

4.1 参数设定

算法参数见表2。

表2 算法参数Table 2 Algorithm parameter value

蜂群参数(种群规模、迭代次数、局部搜索次数)取值对求解结果都有较大影响。本文通过多次测试，确定种群规模NP=50，迭代次数MaxCycle=100，局部搜索次数limit=5，邻域内部搜索次数limit1=50。

4.2 计算分析

根据本文构建的模型和设计的求解算法，计算得到的初始解列车停站方案(按运行图中时间顺序排列)如图4 所示，初始解列车运行图如图6 所示。优化后最优解列车停站方案(按运行图中时间顺序排列)如图5所示，优化后列车运行图如图7所示。初始解与最优解结果对比如表3所示。

图4 初始解列车停站方案Fig.4 Initial solution of train stopping plan

图5 最优解列车停站方案Fig.5 Optimal train stopping plan

图6 初始解列车运行图Fig.6 Initial train operation diagram

图7 最优解列车运行图Fig.7 Optimal train operation diagram

表3 初始解与最优解结果对比Table 3 Initial solution is compared with the optimal solution

与初始解相比：

1) 在满足客流需求的条件下，列车停站总次数减少了10.9%；

2) 列车越行时间增加了61 min，越行时间的增多是因为在追求运用动车组数量最少这一目标过程中，运行图中运行线小范围集中造成的；

3)初始解所需动车组数量为直达列车4列、择站停列车19 列，最优解所需动车组数量为直达列车2 列，择站停列车14 列。所需直达列车等级的动车组数量减少了50%，所需择站停列车等级的动车组数量减少了26.3%，总体上所需动车组数量减少了30.4%。

5 结论

1) 本文构建的研究模型能够准确描述停站方案与动车组接续之间的制约关系，以及充分体现协同优化的思想，且实例表明模型有效。

2) 对于求解模型的算法，本文针对初始解和邻域的生成进行了算法的设计，实例表明设计的算法高效、准确。

3) 提供了一套行之有效的高速铁路列车停站方案编制的理论方法，为铁路运营工作提供决策支持，能够运用在铁路运输生产的决策工作中。

本文从全局的角度分析了列车停站方案、运行图以及动车组接续之间的关系，使得各个计划之间的联系更加紧密，模型更具有可行性，设计了更贴合模型的人工蜂群算法，实例分析结果显示优化后的各项指标都得到了明显的改进。但由于实际的停站方案考虑的条件更为复杂，如何在进一步满足旅客需求的条件下，实现停站方案的合理编制和动车组的高效利用是今后需要深入研究的方向。