考虑高铁与其它运输方式竞争的停站方案优化
王晓阳,倪少权
(1.西南交通大学交通运输与物流学院,四川 成都 610031;2.综合交通运输智能化国家地方联合工程实验室,四川 成都 610031;3.综合交通大数据应用技术国家工程实验室,四川 成都 610031)
1 引言
目前我国多种综合交通运输方式竞相发展,旅客出行选择的多样化加剧了运输通道内各种运输方式之间的博弈竞争。高速铁路若要在综合交通市场中抢占先机,进而脱颖而出,需要进一步优化运输组织模式。停站方案作为旅客评判高速铁路运输组织服务水平的标准,对其进行优化调整显得尤为重要。
国内外专家学者对停站方案开展了大量的研究。文献[1]提出“列车在重要车站停站,而在相对不重要车站交替停站”的停站策略;文献[2]讨论以输送能力为约束条件的周期列车停站方案;文献[3]构建基于节点服务的高铁停站方案优化模型;文献[4]以提升旅客出行效率为目标设计停站方案混合整数规划模型;文献[5]从列车停站方案均衡性和可达性入手对停站方案进行优化研究;文献[6]以最小化列车总停站次数为优化目标,构建基于不确定客流的停站方案机会约束规划模型;文献[7]将列车牵引能耗和旅行时间作为目标,以既有运输供给为约束建立停站优化模型。
上述研究为本文研究奠定了良好的理论基础,但现有研究都只关注高速铁路一种运输方式。在综合交通运输大体系下,高速铁路在短途运输时与公路博弈激烈,在长途运输时与航空博弈激烈,然而鲜有学者考虑“铁公”和“铁航”竞争条件下对高速铁路停站方案进行优化。鉴于此,本文选取多指标构建效用函数,考虑基于平均效用函数的高铁与其它运输方式的博弈,建立铁路营业收入和效用函数值最大的高速铁路停站方案优化模型,并设计自适应并行模拟退火算法对模型求解。
2 问题描述
高速铁路与公路、民航技术特性差异较大,由此不同运距条件下各运输方式的客运量不尽相同。为提高客运量及旅客收益,各运输方式运营部门在不同运距下会采取不同的运营策略。高速铁路在中途运输保持着巨大优势,为诱增“短途”和“长途”客流,高铁部门采取何种停站策略变得尤为关键。旅客在确定出行起讫点后,将在“时间”、“费用”、“舒适度”等方面综合权衡,进而倾向选择使自己获得最大收益的出行方式,旅客出行选择交通方式过程如图1所示。

图1 旅客出行选择交通运输方式示意图
高速铁路不同停站方案对应不同的效用函数值。因此,问题转化为基于快速性、方便性、舒适性和经济性等指标构建效用函数,考虑不同运距下高铁与其它运输方式的平均效用对比函数优化停站,立足于提升高速铁路部门营业收入以及满足不同运距旅客的差异性旅行需求。
3 模型构建
3.1 模型假设
1)假定高速铁路列车开行对数和列车开行起讫点已知。2)优化方案可能导致少部分高速铁路客流诱增或流失,本研究中忽略不计。3)短途运输航空客流份额占比较少,短途运输仅考虑高铁与公路的竞争;长途运输公路客流占比较少,长途运输仅考虑高铁与航空的竞争。4)研究通道内的道路公交时刻表和航班时刻表已知。
3.2 模型符号说明
集合:设车站集合为S,由h,i,j索引,且i 1)快速性指标 快速性指标主要通过旅客从始发地运行至目的地耗时大小来体现。高速铁路总旅行时间包括进出站时间、途中运行时间、中间站停站时间以及起停车附加时分;道路长途公交不包括起停车附加时分;民航多为直达运输,不包括中间站停站时间和起停车附加时分。旅客从i站运行至j站采用高铁、道路公交和民航三种不同运输方式总耗时计算公式分别如式(1)—式(3)所示。 ∀m∈{1,2},∀km∈Km,∀i,h,j∈S,i (1) ∀km∈Km,∀i,h,j∈S,i (2) (3) 2)经济性指标 经济性指标主要通过旅客选择第m种运输方式的第km次车从车站i运行至车站j所花费的票价来体现,即 (4) 3)舒适性指标 舒适性指标主要通过旅客选择第m种运输方式的第km次车从i站运行至j站的疲劳恢复时间来体现,即 (5) 4)方便性指标 方便性指标主要通过旅客从i站运行至j站可选择乘坐列车的发车频率来体现,即 (6) 对快速性、经济性和舒适性指标按式(7)进行标准化处理,对方便性指标按式(8)进行标准化处理。 ∀m∈{1,2,3,4} (7) (8) 旅客选择第m种运输方式中所有能从i站运行至j站的列车总效用函数值如式(9)所示。 ∀f∈{1,2,3};∀m∈{1,2,3,4},∀km∈Km (9) αf+βf+γf+δf=1 (10) 目标函数1为最大化高速铁路营业部门收入,式(11)第1项表示A类和B类高速列车总客票收入,第2项表示A类和B类高速列车总停站支出,第3项表示A类和B类高速列车总运营支出。 (11) 目标函数2为最大化高速铁路效用函数值,如式(12)所示 (12) 考虑高速铁路短途运输与公路的博弈,长途运输与航空的博弈。从i站运行至j站的高速铁路列车的平均效用函数值在短途运输应不低于道路公交,长途运输应不低于民航飞机,即 ∀i,j∈S,j>i (13) 合理的停站方案设置应能保证最低的客流密度需求,从i站至j站间开行列车的席位数应不少于相应的客流密度,即 ∀i,j∈S,i (14) 不同等级的客流节点对停站率有不同的要求,应保证列车在各车站停站次数不能低于各车站最低停站率要求[3],即 ∀h∈S (15) 从提升高速铁路通过能力和提高列车旅行速度角度出发,应当对列车停站次数上限进行一定的约束,即 ∀m∈{1,2},∀km∈Km,∀i,h,j∈S,i (16) (17) 列车在起、终点站必停,即 (18) 决策变量的取值约束如式(19)所示 (19) 上述模型为多目标0-1整数非线性规划模型,随着实例规模的增大,模型变量急剧增加,解空间的规模随着车站数和列车数的增加呈几何级数递增,即使对小规模的车站数和列车数,也很难在有效时间内找到最优解。基于模型和问题特点,同时兼顾算法的收敛效率,本文设计自适应并行模拟退火算法。 1)多目标转化 上述模型为多目标规划模型,利用权重法将双目标转化为单目标进行求解[7],引入权重系数ω1和ω2,且ω1+ω2=1。同时将极大化问题转化为极小化问题 (20) 2)初始解构造 有研究表明咽峡炎链球菌组虽然致病性强,但敏感性相对更高。青霉素的敏感率在95%以上,对头孢敏噻肟敏感率为100%[1]。本例患者临床感染中毒症状不典型,故选用头孢曲松未联合万古霉素。细菌性脑膜炎的治疗疗程更多是按经验来定,可根据临床效果个体化决定适当疗程。推荐链球菌用药15 d左右[6]。 表1 不同运距条件下αf、βf、γf、δf取值表 按照“一级节点必停、二级节点择客流量大的站点停,三级节点满足列车停站均衡性择站停”的方法随机生成一组满足约束(13)—(15)的解X0,若X0也满足约束(16)—(19),则X0即为初始解。否则,调整二级节点和三级节点的停站,直至满足所有约束。 3)邻域解构造 邻域的构造选择2-opt方法,即将高速铁路初始停站方案中列车在二、三级节点两两之间的停站方案进行对调生成新的停站方案。 4)并行化策略 并行化策略将一条马尔科夫链分裂为m条可以持续遗传和信息交互的子一代马尔科夫链,每个线程获得初始解X0后,子一代马尔科夫链分裂成m条子二代马尔科夫链,子二代马尔科夫链从相同的初温执行退火操作。经过若干次迭代达到中间某个确定的温度时,比较m条子二代马尔科夫链对应的Zp值及局部最优解Xp,如果第mp条马尔科夫链对应的Zp值最小,则在下一温度水平下,将当前的局部最优解Xp作为各个线程的初始解,第mp条马尔科夫链继续执行分裂操作。若有超过两个以上的局部最优解,任选一个即可。 5)自适应机制 自适应机制是指不同亲代的子代马尔科夫链降温至指定温度时,不同子代之间进行信息交流局部最优解。在同一温度水平t下,子代基于亲代在上一步的解和邻域局部最优解,按照Metroplics准则更新当前解。 Step2:生成初始解,根据3.1节(2)中的方法生成高速铁路初始停站方案,并计算初始解目标函数值Z0。 Step3:并行化操作,亲代的一条马尔科夫链分裂为m条可以持续分裂和信息交互的子马尔科夫链,各子代马尔科夫链独立地并发执行模拟退火操作。 Step8:调整模拟退火温度t=αt。 Step9:自适应操作,温度达到指定温度t*时,不同子代之间进行信息交流局部最优解,子代基于亲代在上一步的解和其它m-1条马尔科夫链的局部最优解,按照Step6准则更新当前解。 Step10:收敛性检验,若t≤te,则算法终止,比较m条亲代马尔科夫链对应局部最优解的值,从局部最优解中选择全局最优解。否则m条亲代马尔科夫链继续分裂并重复Step3~Step9。 以京沪高铁为优化研究对象,将其沿线23个车站作为基准站,查阅相关资料可得道路公交和民航时刻表,限于篇幅不再展示。 案例选取2020年京沪高铁四季度某日上行列车运行图和实际客流数据。其中本线全程车36列,本线区段列车74列,跨线列车183列。模型中所需各参数均按运行图系统中的实际数据取值。 应用Matlab R2020b执行自适应并行模拟退火操作,计算机配置为Intel(R)Core(TM)i5-8250UCPU(1.80 GHz)、8.00GB。计算机在运行120s,算法迭代50多次达到稳定值。限于篇幅仅展示优化后的全程列车停站方案分别见图2,算法迭代收敛图见图3。 图2 优化后京沪线全程列车停站示意图 图3 迭代次数收敛图 优化后短途列车停站频率得到提升,中途列车停站频率略有减少,长途列车停站频率显著减少。究其原因,可能是由不同运距条件下旅客对快速性和舒适性等指标的偏好不同造成的。因此,停站方案优化应当考虑“短途列车增加停站,中途列车择优停站,长途列车减少停站”的原则。不同运距列车停站次数优化前后对比如表2所示。 表2 不同运距列车停站次数优化前后对比 初始停站方案中,2020年第四季度图某日的上行京沪线列车中间站停站全日共计1294次,优化后全日共计停站1159次,优化方案使得停站次数显著减少,旅客旅行时间明显缩短。同时目标函数值进一步优化,其中铁路部门营业收入提高10.6%,综合效用值提高15.1%。 为提升高速铁路在综合交通运输市场中的竞争力,建立以高铁与其它运输方式平均效用对比函数等为约束的非线性整数规划模型,并设计自适应并行模拟退火算法求解,最后以京沪高铁为例进行停站优化。仿真结果表明:优化后短途列车停站频率得到提升,中途列车停站频率略有减少,长途列车停站频率显著减少。同时,高铁部门营业收入和高铁效用值得到明显提高。所提方法可以为高速铁路管理部门在停站方案制定方面提供合理参考和科学依据。
3.3 各运输方式效用函数




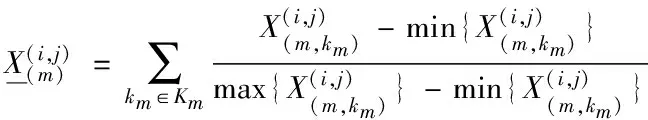

3.4 目标函数

3.5 约束条件


4 自适应并行模拟退火算法设计
4.1 算法关键步骤设计



4.2 算法实施步骤


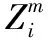


5 实例分析
5.1 数据准备

5.2 模型求解


5.3 优化结果分析

6 结论

