不锈钢钢筋混凝土梁动态损伤试验与数值模拟

周锡武，汪祥宇，张稳，张文超

(1. 佛山科学技术学院 交通与土木建筑学院，广东 佛山 528000；2. 广西大学 土木建筑工程学院，广西 南宁 530000；3. 同济大学 土木工程学院，上海 200092）

随着国内外港口码头和跨海大桥等海洋工程的迅速发展，海工混凝土结构不可避免地面临船舶、海浪冲击等随机事故以及耐腐蚀问题，配置高强度以及耐腐蚀性强的不锈钢混凝土结构已成为发展趋势[1]，因此，开展不锈钢混凝土构件在冲击荷载下力学行为的研究具有重要的意义。钢筋混凝土梁构件是混凝土结构的重要组成部分，很多学者对梁的抗冲击行为进行了一系列研究。KI‐SHI等[2]提出了基于静态力学性能的RC梁抗冲击经验公式，并发现采用最大支座反力来评估梁的抗冲击能力更合理。许斌等[3]通过落锤冲击试验研究RC 梁的动态响应以及力学行为，重点分析裂缝的发展以及破坏模式的变化，并认为用冲击力和支反力描述梁的抗冲击承载力特征值均不准确。LEE等[4]研究钢纤维混凝土梁的抗冲击力学性能，发现加入钢纤维提高了梁的承载力、吸能能力、降低了残余位移。赵武超等[5]针对冲击荷载下梁局部具有持时短暂和效应明显等特征，提出基于截面损伤因子的损伤评估方法。赵德博等[6]通过试验研究发现随着冲击速度的提高，落锤动能更多地用于梁局部损伤消耗，整体耗能比例减小，并提出了估算冲击荷载作用下梁最大挠度的经验公式。PHAM 等[7]通过试验和数值模拟提出移行塑性铰的概念以及一种推导钢筋混凝土梁剪力和弯矩图的方法。赵武超等[8]通过数值模拟指出，只有在局部响应阶段梁不发生剪切破坏的前提下，才能保证整体响应阶段的弯曲破坏，同时局部响应阶段的损伤程度也会对整体响应阶段的承载能力产生影响。ZHOU 等[9]通过不锈钢等强度代替RC 梁的落锤冲击试验发现，当配筋率较小时，采用等强度替代的SRC 梁可以减少累积冲击后的刚度损失，提高梁的抗冲击能力。然而不锈钢钢筋本身延性，强度、塑性与普通钢筋不同，且没有明显的屈服点，因此SRC 梁在冲击荷载下的损伤行为需进一步研究。本文采用国内先进超高重型落锤冲击试验系统，分别对RC 梁和等截面纵筋代替的SRC 梁进行竖向冲击试验。结合有限元模型研究SRC 梁的损伤行为，为SRC 梁的抗冲击设计和已有结构的抗冲击能力评估提供技术支持。

1 试验概况

1.1 试件设计及试验方法

本次实验共设计了6根钢筋混凝土梁试件，梁长2 000 mm，净跨1 800 mm，截面尺寸b×h=150 mm × 300 mm，保护层厚度25 mm，混凝土强度等级C40，实测标准立方体试块平均抗压强度45.3 MPa。箍筋采用普通钢筋HPB300，屈服强度302 MPa，架立筋采用普通钢筋HRB400，屈服强度420 MPa。

试件梁分为A 和B 2 组，A 组为RC 梁(编号用C)，底筋采用普通钢筋HRB400；B 组为等截面底筋代替的SRC 梁(编号用S)，采用由法国UGI‐TECH 公司生产的S2304 双相不锈钢钢筋(UGI‐GRIP1. 4362)，屈服强度893 MPa。试件采用模板浇筑，人工振捣，并在室温下养护28 d，梁截面配筋如图1所示。

图1 C16梁配筋Fig.1 Reinforcement drawing of C16 beam

本试验落锤质量为400 kg，依次将落锤提升至1.0 m 和1.5 m，对梁C16 与S16 进行累积2 次撞击实验，对其余梁进行单次撞击试验。实验设计见表1。

表1 实验设计Table 1 Experimental design

1.2 试验装置及数据采集

采用国内先进超高落锤冲击实验系统对试件进行竖向冲击试验，装置如图2所示。落锤锤头为直径200 mm 的圆柱体，将梁试件放置在落锤下方铰支座上，为防止受冲击反弹，在梁端上方布置压板并用螺杆与支座相连。通过液压装置将落锤提升到指定高度，松开夹具，落锤沿竖向导轨近似做自由落体运动，撞击梁跨中位置。落锤下落的瞬时速度由布置在导轨末端的激光测速装置测得。当锤头与梁接触时，落锤瞬时速度发生变化，数据采集在此时触发。跨中挠度由布置在梁跨中的KTC-200 拉杆式位移计测得。用裂缝测宽仪测量撞击后梁损伤裂缝的宽度，并采用高速摄像机对冲击试验过程进行记录。

图2 落锤冲击试验装置Fig.2 Drop weight impact test device

2 实验结果分析

2.1 位移时程分析

试验的位移时程曲线由梁跨中底部的位移计测得，各组位移数据如表2，其中D为跨中峰值位移，δ为残余位移。

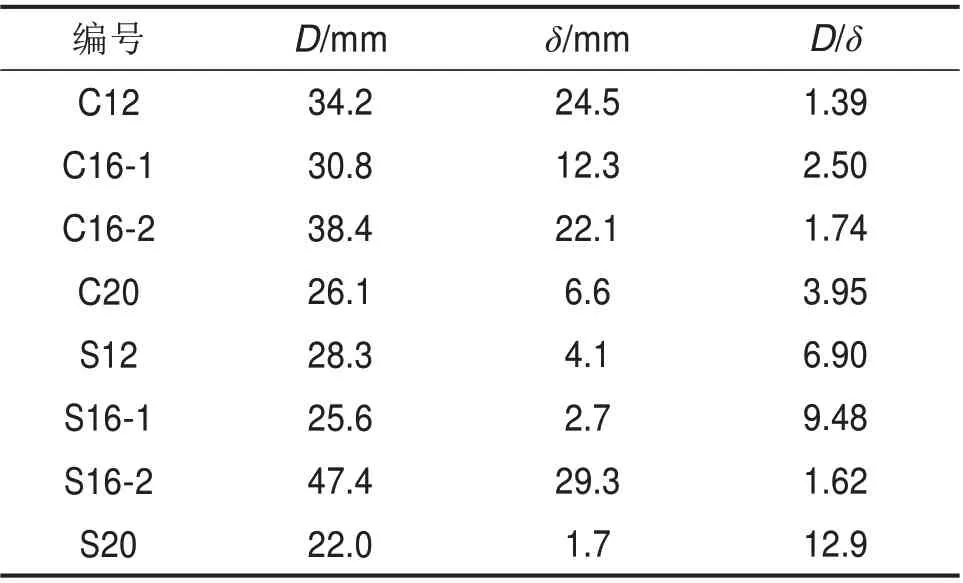
表2 位移数据Table 2 Displacement data

梁的位移时程曲线如图3所示，把配筋率相同的RC 与SRC 梁的位移时程曲线归并到同一幅图中，将冲击开始时刻定义为0 时。落锤与梁碰撞后，梁受冲击力作用向下加速运动，跨中位移逐渐增大，到达峰值后迅速下降，形成一个主波峰，随后位移下降到最小值后上升，形成一个波谷，位移上升到一定值后曲线趋于水平，碰撞过程结束。RC 与SRC 梁的跨中位移时程发展趋势类似。由图3可知，配筋相同的情况下，由于不锈钢钢筋强度高，首次撞击SRC 梁的峰值位移均低于RC梁；同时由试验测得梁S12和C12跨中钢筋残余应变分别为0.000 4，0.004 8，梁S12钢筋基本没有屈服，弹性恢复明显，而梁C12 钢筋塑性变形较大，因此梁S12 首次冲击所造成的残余位移较梁C12小，其他配筋率相同的SRC 梁与RC 梁情况类似。配筋率从0.58%提高到1.63%，梁试件峰值和残余位移均逐渐减小；由表2 对跨中峰值位移(D)与残余位移(δ)的比值分析发现，SRC 梁与RC 梁在相同冲击能量下，随着配筋率的减小，峰值位移与残余位移比值均逐渐减小。KISHI 等[2]在进行梁的抗冲击设计时，提出峰值位移与残余位移关系D≈1.5δ，本试验发现，RC 梁的损伤程度较大且接近于完全破坏时，D与δ的比值接近于1.5倍。

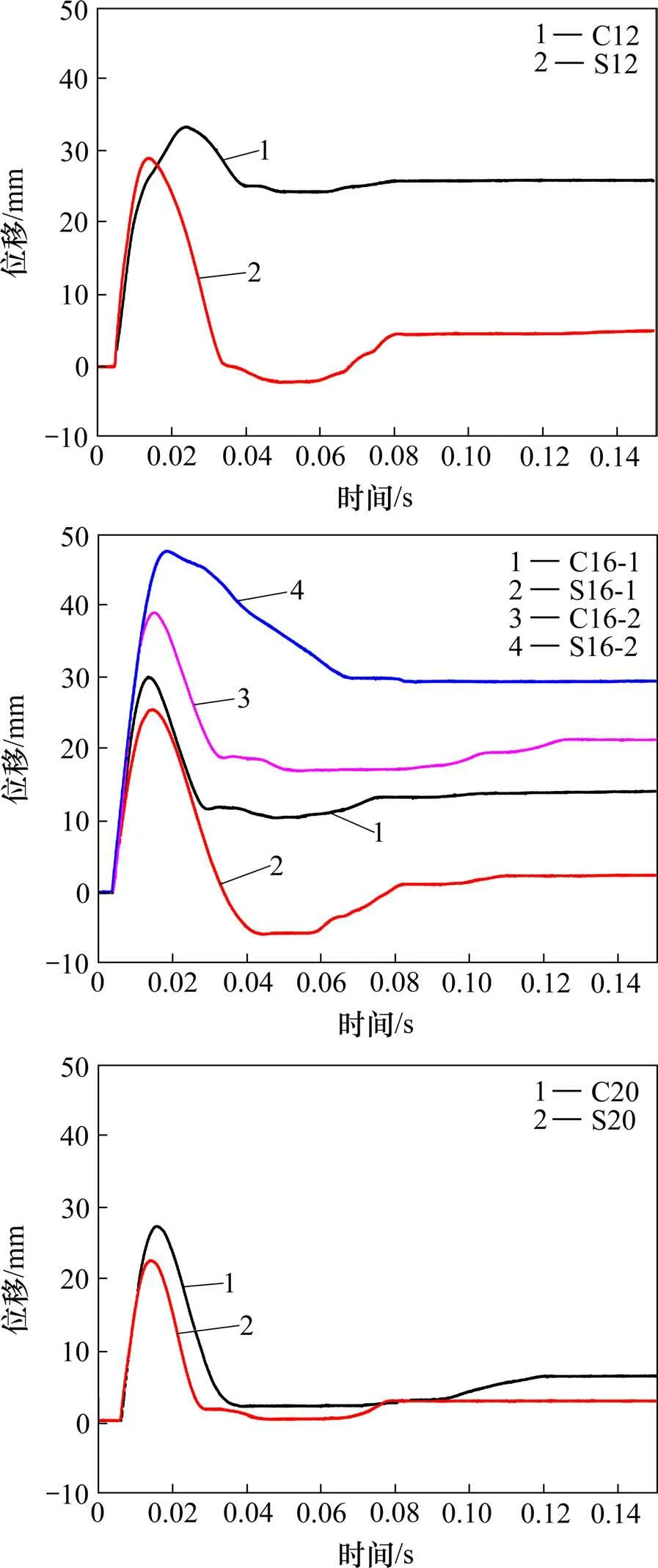
图3 位移时程曲线Fig.3 Displacement time history curves

第2 次撞击梁C16 与S16 的位移时程发展趋势与第1 次撞击大致相同，但梁S16-2 峰值及残余位移均高于梁C16-2。主要原因为第1 次撞击结束后SRC 梁的残余位移远小于峰值位移，不锈钢钢筋的塑性变形耗能较小，能量较多的作用于混凝土损伤和变形消耗上。在第2次撞击时，不锈钢钢筋承担的能量消耗增大，因此不锈钢钢筋的塑性变形得以充分发挥，同时(如图4)梁S16-2表现为脆性破坏，所以SRC 梁大于RC 梁第2 次撞击的峰值和残余位移。不锈钢钢筋没有明显的屈服点，且表现较好的延性，若用位移评价梁的抗冲击承载能力，SRC梁的最大极限位移要高于RC梁的。

2.2 损伤破坏分析

各试件的最终裂缝分布如图4所示，本文定义跨中梁锤接触区域的损伤为局部破坏，应力波未传至支座前为局部响应阶段。由图4 可知第1 次冲击结束后，等截面代替的SRC 梁整体损伤程度低于RC 梁。梁跨中均产生较明显的局部破坏，但随着配筋率的提高，梁抗弯强度提升，局部弯曲裂缝逐渐消退，局部冲切裂缝发展减弱；梁的抗剪强度增长不显著，整体剪切裂缝的发展没有受到抑制，梁整体破坏模式由延性弯曲破坏向脆性剪切破坏发展。梁C12裂缝形态主要由弯曲裂缝、局部冲切裂缝和整体剪切裂缝组成，且局部区域的损伤最严重；而梁S12整体变形耗能较低，能量更多地作用于混凝土的裂缝开展，因此裂缝发展较为充分。累积撞击下，第2次撞击速度为4.52 m/s，SRC 梁与RC 梁的裂缝均基于第1 次撞击进一步发展，梁C16局部混凝土脱落严重，端部截面与整体错位，钢筋弯曲；梁S16跨中混凝土与两端脱离且发生较大的错位，钢筋变形，接近于完全损伤，失去继续承载的能力。

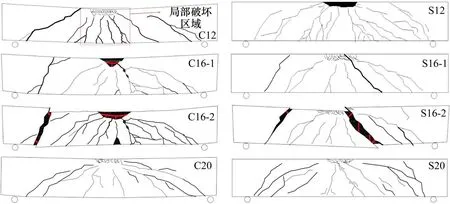
图4 试件最终裂缝分布Fig.4 Final crack distribution of specimen

3 数值模拟

3.1 模型建立及材料参数

为了进一步研究冲击荷载作用下梁的局部破坏和整体损伤，采用有限元软件Abquas 显示动力学模块对上述试验进行三维数值模拟，数值模型如图5。锤头简化为圆柱体，半径为200 mm，冲击位置在跨中，可通过修改材料密度来控制落锤质量。约束落锤使其仅在竖向发生位移。并通过预定义场设定落锤冲击速度。支座简化为图1所示矩形框结构来模拟试验过程中梁上部的压板，并与梁之间固结。在支座正下方设置耦合点约束支座的竖向位移。落锤和支座定义为刚体。不考虑钢筋与混凝土之间的黏结滑移。落锤与梁以及梁与支座的接触设置为通用接触。 混凝土选用三维八结点线性减缩积分实体单元C3D8R，并且引入单元沙漏控制，钢筋采用三维桁架单元T3D2，网格划分时近似全局尺寸为25 mm。

图5 数值模型Fig.5 Numerical model

混凝土采用Abquas 中提供的损伤塑性模型(CDP)，该模型可以分析在动态加载和单调、循环加载条件下混凝土结构的力学响应，考虑材料拉压性能的差异，不仅能描述混凝土的不可逆损伤，而且还可以描述材料的刚度退化行为[10]。普通钢筋本构采用双线性弹塑性模型[11]。不锈钢钢筋本构采用Johnson-Cook模型[12]。

采用欧洲国际混凝土委员会(CEB)[13]所提出的混凝土抗拉强度动态放大系数(TDIF)，和混凝土抗压强度动态放大系数(CDIF)模型来表征混凝土率效应。同时引入cowper-symond 模型[14]来表征普通钢筋的率效应，其表达式为ḟy/fy= 1+(ε̇/D)1/P，模型假定不随应变强化效应而改变，其中D和P的取值与钢筋的极限强度有关，本文分别取为40和5。

3.2 模型验证

对各试件的冲击力峰值与跨中位移峰值试验与数值模拟结果统计如表3 所示，由表3 可知冲击力峰值最大误差不超过20%，跨中位移峰值最大误差不超过25%，由于试验条件下存在摩擦耗能状况，该误差在允许范围内，由此可说明数值模拟结果良好。

表3 试验与数值模拟数据对比Table 3 Comparison of experimental and numerical simulation data

4 数值模拟结果分析

本文数值模拟主要研究冲击荷载下不锈钢混凝土梁整体损伤发展、冲击作用前期的内力分布。

4.1 损伤发展分析

梁S12 的模拟损伤发展历程如图6 所示，梁锤撞击可分为局部响应阶段和整体响应阶段，在局部响应阶段，梁受锤冲击，接触部位首先发生撞击损伤，且梁锤接触部位为受压区混凝土，受压区混凝土的损伤会导致梁的抗弯能力下降，进而影响梁的破坏模式。然后应力波向下和左右两端传播，在未传到支座之前，支座与梁连接部分未受到冲击荷载的影响，可看作固定铰支座，这样使梁的受荷跨度降低，集中在跨中的局部区域，梁跨中的抗弯强度随受荷跨度减小提升，因此受冲击荷载的梁在跨中区域主要形成剪切破坏的斜裂缝，并在局部范围内呈八字形，这是梁在冲击荷载下独特的剪切效应，并主要作用于局部响应阶段。当应力波传至支座后，梁受惯性力和支反力共同作用，整体开始向下移动，此时才是决定梁整体破坏模式的关键，若惯性力与支反力的合力大于梁整体的抗弯承载力则梁发生弯曲破坏，反之则发生剪切破坏，若合力既大于梁的抗弯能力又大于梁的抗剪能力则梁发生弯剪破坏。图6梁破坏模式为弯剪破坏，但剪切破坏的程度要高于弯曲破坏。因此局部的冲切破坏并不完全代表梁整体的破坏类型。

图6 梁S12损伤发展历程Fig.6 Damage development course of beam S12

4.2 局部响应阶段梁内力分析

在局部响应阶段，梁主要受冲击力和惯性力作用。梁因应力波扰动被激活区域会产生向下的加速度，未被扰动区域约束扰动区域的运动。在冲击作用前期落锤的冲击能量主要被局部破坏消耗，因此在冲击荷载作用下，梁局部破坏最严重且最先发生。结合有限元取沿梁长度方向取对称位置的7 个测点做加速度时程分析，测点布置如图7。

图7 加速度测点布置图Fig.7 Layout of acceleration measuring points

把A1～A4 的4 个测点的加速度时程曲线归并到一张图上，由图8可知，梁锤接触后，跨中测点A1 的加速度最先出现且数值最大，随着应力波的传播，后续测点由跨中到支座方向相继出现且加速度值越靠近支座越小，从而证明梁沿长度方向的加速度具有一定的传导过程。把梁时程上每点的加速度沿梁长度方向用曲线连接，得到如图9所示的历程分布图，可见在0.4 ms左右时加速度还未传至支座附近的梁段。

图8 加速度时程图Fig.8 Acceleration time chart

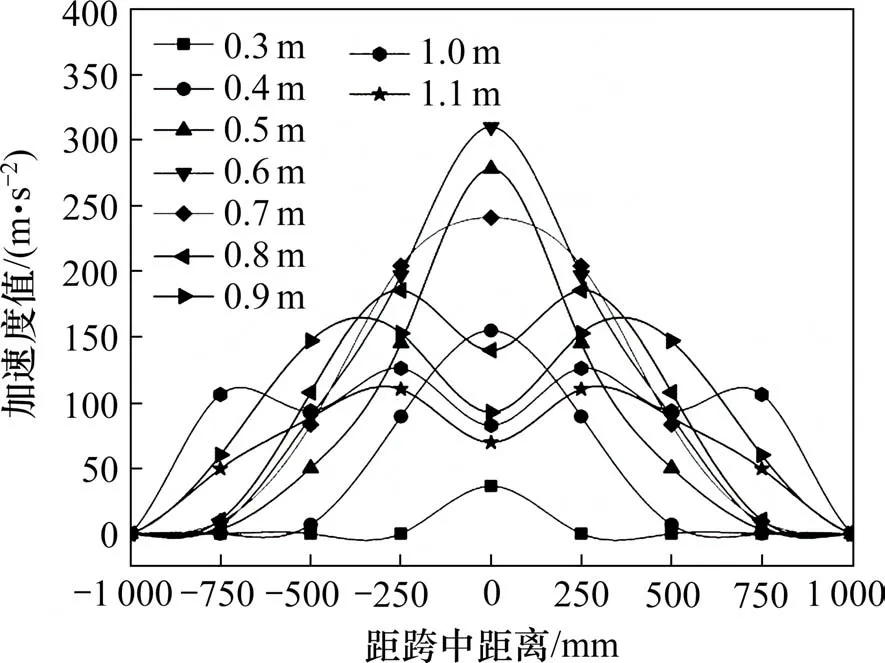
图9 加速度沿梁长度方向的历程分布图Fig.9 History distribution of acceleration along the length direction of beam

梁向下运动会产生向上的惯性力，其大小等于质量在体积上的积分与加速度相乘，通用公式[15]为：

PHAM 等[7]认为，在局部响应阶段，应力波未传至支座之前，大约有2/3 的冲击力转化为惯性力。本文发现，未因应力波扰动被激活区域的梁段约束了扰动区域梁向下的加速运动，如图10 所示。因此，梁未激活区域在失效之前可看做固定端支座，与冲击力、惯性力形成平衡力系，共同作用于梁冲击过程中的局部响应阶段。YI 等[16]发现在应力波未传到支座之前可假定惯性力沿梁长度方向近似为线性分布，因此可简化为图11 所示局部响应阶段梁的计算模型。

图10 局部阶段梁的动态响应Fig.10 Dynamic response of beam in local stage

图11 梁受力简图Fig.11 Beam stress diagram

取惯性力I约等于2/3冲击力P，从梁扰动区域左端计算截面的弯矩M和剪力V，可以表示为：

式中：2a为梁扰动区域长度，主要与冲击速度、梁长有关；q为惯性力线荷载最大值；x为计算截面与梁扰动区域左端的距离。

上述经验公式主要应用于冲击作用前期，取这一时段的截面剪力和弯矩作为研究对象，由经验公式绘出梁扰动区域的内力分布如图12，这与文献[3]分析得到的梁整体内力分布图相吻合。同时，结合文献[3, 6]，图4 和图6 梁的损伤分析发现，梁跨中在冲击初始时刻首先产生破坏，并在冲击结束后成为主要损伤区域，以剪切斜裂缝呈现，说明冲击荷载作用下梁跨中主要受剪力作用。

图12 梁内力分布图Fig.12 Beam internal force distribution diagram

总体来看，经验公式得出梁的内力分布图中，梁扰动区域的有效跨度较梁净跨小，且由于惯性力和固定端负弯矩的存在，使得梁跨中所受弯矩减少，从而减轻梁的弯曲破坏；同时，扰动区域内跨中剪力最大，并沿梁长度方向逐渐减小，因此跨中区域主要以剪切破坏为主。

5 结论

1) 等截面代替后的SRC 梁的跨中位移减小，开裂程度降低，梁的抗冲击能力提升；但配筋率较大时，不锈钢钢筋塑性损伤较小，变形耗能也小，更多的能量被混凝土变形和损伤消耗，梁整体破坏模式由延性弯曲破坏向脆性剪切破坏发展。

2) 梁配筋率增加和不锈钢钢筋替代普通钢筋都能有效的抑制跨中底部竖向裂缝的发展；峰值位移与残余位移的比值随着梁损伤程度的加重逐渐减小。本实验当梁接近完全损伤时，D/δ≈1.5；冲击荷载下，SRC 梁的最大极限位移要比普通混凝土梁延后。

3) 剪切效应主要作用于梁的局部响应阶段，使梁产生局部的冲切破坏；局部的冲切破坏并不完全代表梁整体的破坏类型，整体的破坏类型主要取决于梁的抗弯抗剪能力是否能承受局部破坏后剩余的冲击荷载。结合有限元作出梁在冲击荷载下的加速度分布，通过分析得出局部响应阶段梁内力计算的经验公式。