不同摩擦系数下双凹面摩擦摆支座耗能性能的研究
陈章伟,董锦坤,李 茜,窦存杰
不同摩擦系数下双凹面摩擦摆支座耗能性能的研究
陈章伟1,董锦坤1,李 茜2,窦存杰1
(1.辽宁工业大学 土木建筑工程学院,辽宁 锦州 121001;2.中交路桥北方工程有限公司,北京 100024)
利用有限元软件ABAQUS对双凹面摩擦摆支座上、下滑动面摩擦系数不相等施加了竖向荷载以及正弦位移荷载,得到不同摩擦系数下双凹面摩擦摆支座的滞回曲线、临界位移曲线以及支座残余位移。通过对模拟结果分析可以得到双凹面摩擦摆支座临界位移与支座摩擦系数呈线性关系;支座的耗能能力随着摩擦摆支座摩擦系数增大而增大,支座的恢复能力随着支座摩擦系数增大而减小。
有限元;滞回曲线;临界位移;残余位移
摩擦摆支座的整体概念是在1985年由Zayas首次提出[1]。摩擦摆支座以构造简单、施工简便、造价低以及承载能力大、抗平扭能力强、良好的稳定性和自复位能力、耐久性好等优点得到了国内外学者的普遍关注[2]。近年来,国内外学针对摩擦摆支座的材料、结构设计、力学性能等方面做了相应的研究。2016年,龚健[3]对摩擦摆力学模型进行了分析与探讨,并提出了FPB各模型的优缺点以及适用范围。2018年,李晓东等[4]采用超高分子聚乙烯(MSM)为膜材材料分析对比了润摩擦以及干摩擦的耗能性能。2006年,Fenz等[5]分析了双凹面摩擦摆支座的力学性能。本文对双凹面摩擦摆支座的上、下滑动面采用不同的摩擦系数,分析对比双凹面摩擦摆支座的滞回曲线、临界位移以及残余位移等性能,得到支座刚度、耗能性能、临界位移的影响规律[6]。为双凹面摩擦摆支座不同摩擦系数的设计提供了相应参考。
1 支座模型建立
采用大型有限元软件ABAQUS通过旋转建模方式对双凹面摩擦摆支座建立三维实体模型[7-9]。摩擦摆支座的滑动面半径1=2=1 250 mm。有限元三维实体模型具体构造如图1所示。
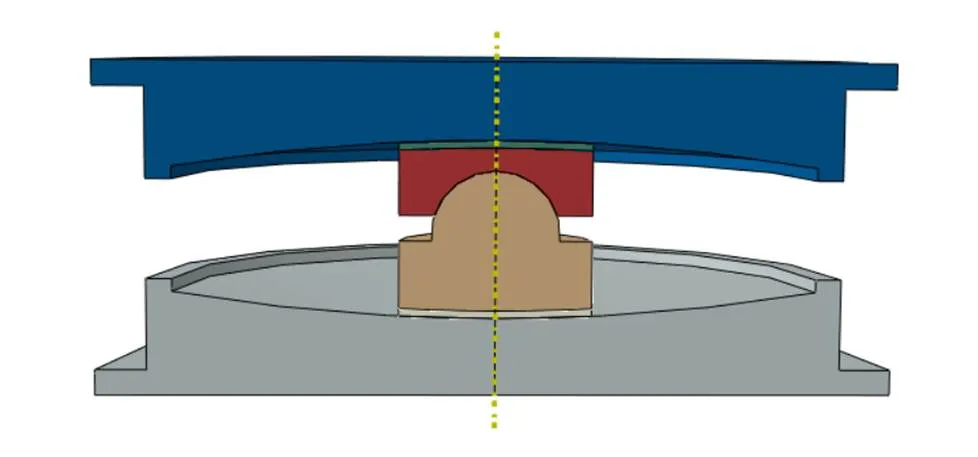
图1 双凹面摩擦摆支座三维实体模型
支座模型主要分为6个部分,即上支座板、耐磨材料、凹球面、凸球面、耐磨材料以及下支座板。其中上支座板、下支座板、凸球面与凹球面组成的铰接滑块采用Q345钢,耐磨材料采用改性超高分子质量聚乙烯(UHMWPE)。Q345钢材的弹性模量为2.1×105MPa、泊松比为0.3;UHMWPE的弹性模量为850 MPa、泊松比为0.42。通过有限元软件对支座施加400 kN的竖向荷载以及最大水平位移为300 mm的水平位移荷载。改变双凹面摩擦摆支座的上、下滑动面摩擦系数,分析支座滞回曲线、临界位移、残余位移等性能。支座滑动面摩擦系数设计实验模型参考表1。
表1 摩擦系数不等的双凹面摩擦摆支座
实验模型编号µ1µ2 10.060.03 20.060.04 30.060.05 40.070.04 50.070.05 60.080.05
2 支座滞回曲线分析
依据实验模型建立6组有限元实体模型。采用对照组实验将模型分为3组。第一组:模型1、模型2、模型3;第二组:模型1、模型4、模型6;第三组:模型3、模型5、模型6。各组试验模型滞回曲线如图2(a)、(b)、(c)所示。
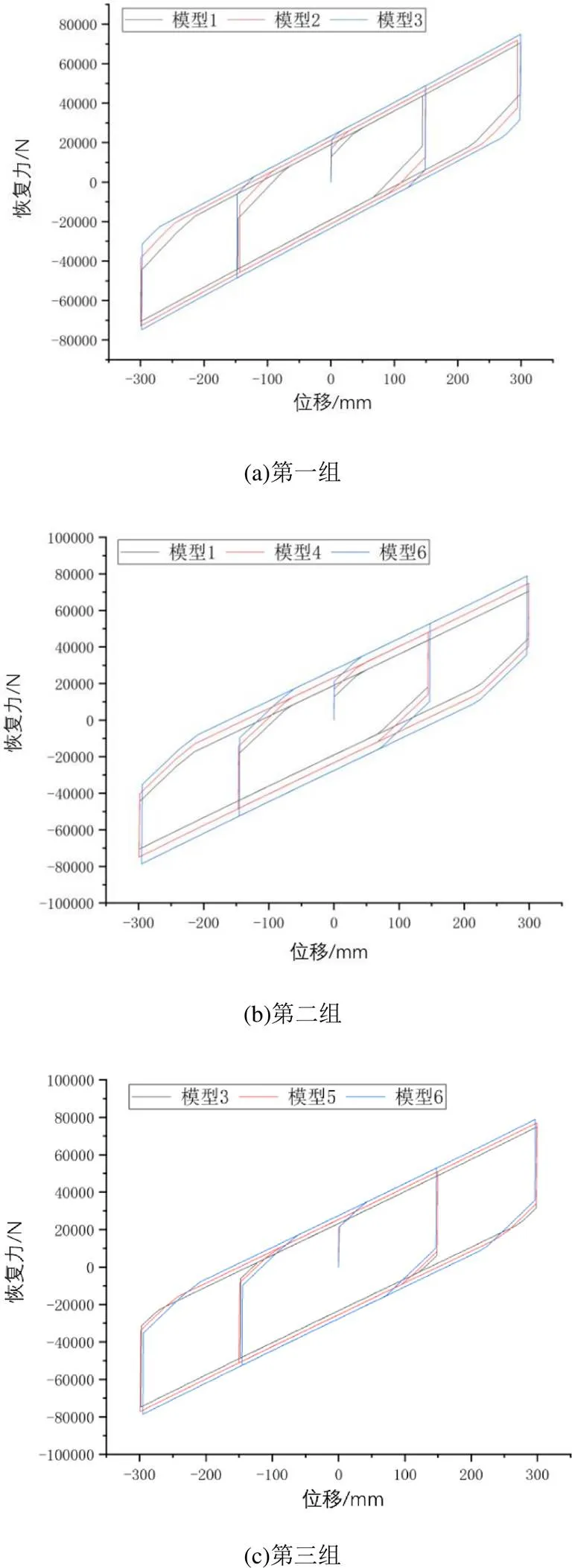
图2 各组试验支座滞回曲线对比图
3组对照实验组模型滞回曲线较为饱和,支座耗能性较好。分析图2(a)、(b)、(c)可得第一组支座刚度r2分别为341.24、348.87、340.02,支座刚度re分别为172.02、172.47、172.58;第二组支座刚度r2分别为341.24、345.07、344.97,支座刚度re分别为172.02、172.43、172.95;第三组支座刚度r2分别为340.02、342.41、344.97,支座刚度re分别为172.58、172.95、172.95。各组支座的刚度基本相同,最大误差2.5%。图中也可观察得到各曲线基本平行。支座滑移位移小于临界位移时,支座等效于单球面摩擦摆支座,此刻支座刚度、隔震周期只与2(滑动面摩擦系数较小的半径)有关。滑移位移大于临界位移时,支座上、下滑动面共同作用。支座的刚度与e(双凹面摩擦摆支座等效半径)有关。对比各组支座滞回曲线,支座滞回环随着摩擦系数增大而增大,即支座的耗能性能越佳。
3 临界位移
依据有限元分析结果得到各试验模型支座的临界位移。图3所示为试验模型1、模型2、模型3临界位移云图。临界位移分别为35.03、21.10、10.96 mm。
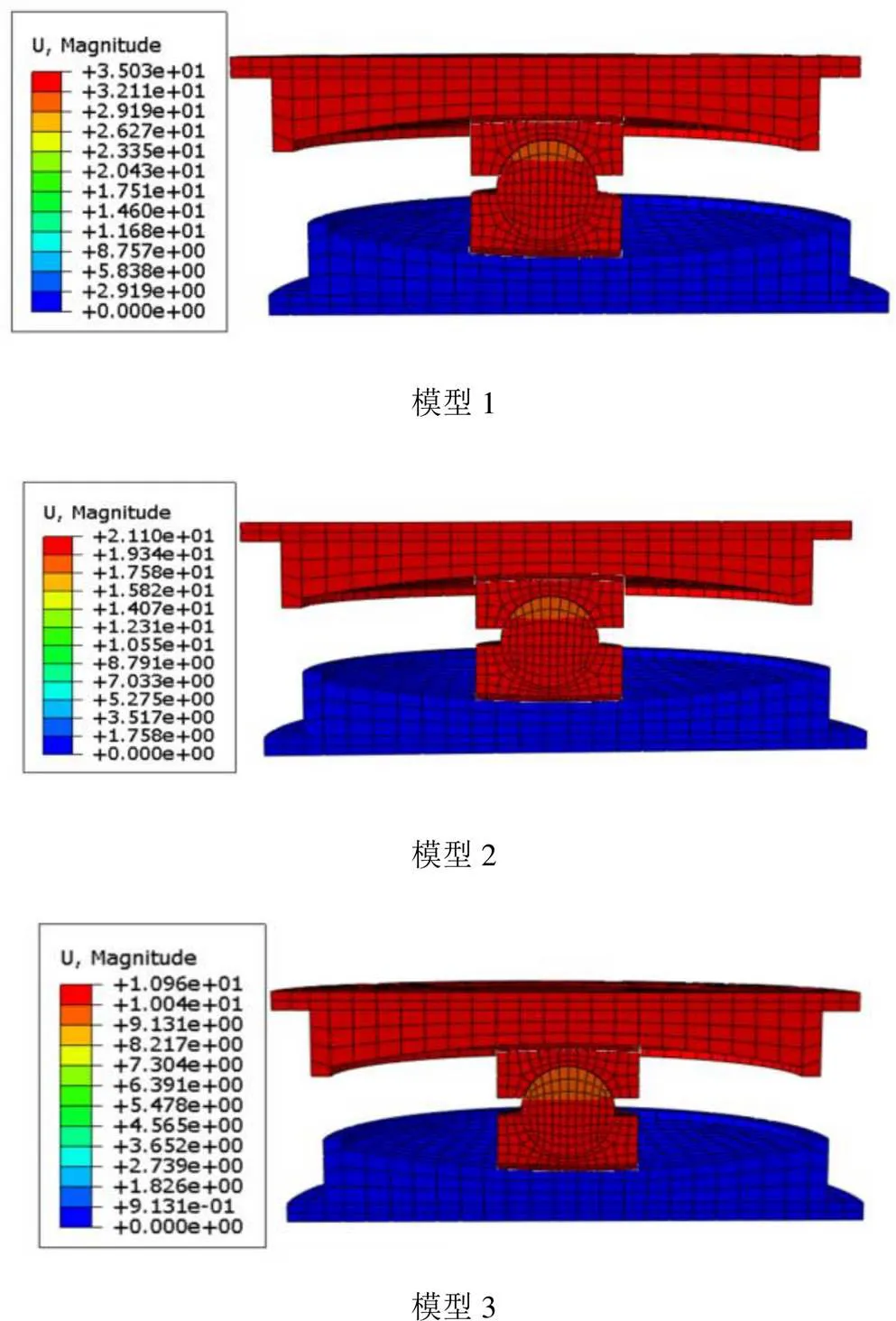
图3 支座残余位移图
对比各组试验模型的临界位移值,绘制点线图。如图4所示。

图4(a)所示支座上滑动面摩擦系数固定,下滑动面摩擦系数逐渐增大,支座的临界位移随着下滑动面摩擦系数的增大而减小。图4(b)各试验支座上、下滑动面摩擦系数均改变,但是上下滑动面摩擦系数差值相等,支座的临界位移也几乎相同。图4(c)各试验支座的下滑动面摩擦系数不变,随着上滑动面摩擦系数的增大,支座临界位移也随之增大。
4 支座残余位移
支座残余位移是衡量摩擦摆支座恢复能力的指标。对于摩擦摆支座不仅要提高支座的耗能性能,也要提高支座的恢复性能。在设计支座时需要更好地衡量支座摩擦系数以达到最佳性能。图5为试验支座1、2、3残余位移云图。

其余支座残余位移数值可参考表2。
表2 各试验支座残余位移与理论值对比
试验模型编号模拟数值/mm理论数值/mm误差值/% 1112.50112.500 2125.10125.000.08 3137.40137.500.07 4137.40137.500.07 5149.70150.000.20 6162.30162.500.12
由表2可得,双凹面摩擦摆支座残余位移模拟值与理论值误差值最大仅有0.2%。可能由于网格划分方式导致计算结果产生的误差。理论值可依据公式=11+22计算。当支座隔震周期固定时,支座残余位移随着支座摩擦系数增大而增大,即支座的恢复能力越低。
5 结语
通过上述模拟分析可得如下结论。
(1)对于不同摩擦系数的双凹面摩擦摆支座滑移位移小于临界位移时支座的刚度以及隔震周期只与支座滑动面摩擦系数较小的半径有关。滑移位移大于临界位移时,支座的刚度以及隔震周期与支座等效半径有关。
(2)支座的临界位移受到摩擦系数的影响,当支座1大于2时,不改变1,支座临界位移随着2的增大而减小;当2为定值,支座临界位移随着1增大而增大。
(3)双凹面摩擦摆支座残余位移与支座滑动面半径以及摩擦系数有关,残余位移随着支座摩擦系数以及半径增大而增大。
(4)对于双凹面摩擦摆支座需要合理衡量滞回耗能、临界位移、残余位移之间关系。使结构在小震作用下,支座等效为单球面摩擦摆支座时具有良好的耗能性能以及恢复能力。
[1] Zayas V A, Low S S, Mahin S A. A Simple Pendulum Technique for Achieving Seismic Isolation[J]. Earthquake Spectra, 1990, 6(2): 317-333.
[2] 庄军生. 桥梁减震、隔震支座和装置[M]. 北京: 中国铁道出版社, 2012.
[3] 龚健. 摩擦摆隔震支座力学模型的探讨[J]. 工程建设与设计, 2016(9): 38-40, 44.
[4] 李晓东, 火娟, 赵健. 摩擦摆支座力学性能探究与其应用分析[J]. 建筑结构, 2018, 48(19): 86-90.
[5] Fenz D M, Constantinou M C. Behaviour of the double concave Friction Pendulum bearing[J]. Earthquake Engineering & Structural Dynamics, 2006, 35(11): 1403-1424.
[6] 夏俊勇, 宁响亮, 吴滔, 等. 双凹摩擦摆支座的设计验证及应用[J]. 铁道建筑, 2016(6): 23-26.
[7] 石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2006: 9-51.
[8] 曹金凤, 石亦平. ABAQUS有限元分析常见问题解答[M]. 北京: 机械工业出版社, 2009.
[9] 冷新云, 夏俊勇, 郭红峰, 等. 摩擦摆支座结构设计及验证[J]. 铁道建筑, 2013(5): 45-48.
Study on Energy Dissipation Properties of Friction Pendulum Bearing with Double Concave Surface under Different Friction Coefficients
CHEN Zhang-wei1, DONG Jin-kun1, LI Qian2, DOU Cun-jie1
(1.School of Civil and Architectural Engineering, Liaoning University of Technology, Jinzhou 121001, China;2.Road & Bridge North Engineering Co., LTD, Beijing 100024, China)
In this paper, the finite element software ABAQUS is used to apply vertical load and sinusoidal displacement load to the unequal friction coefficients of the upper and lower sliding surfaces of the double-concave friction pendulum bearing, and the hysteretic cycle curve, critical displacement curve and residual displacement of the bearing under different friction coefficient are obtained. By analyzing the simulation results, it can be obtained that the critical displacement of the friction pendulum bearing on the double concave surface has a linear relationship with the friction coefficient of the bearing. The energy dissipation capacity of the support increases with the increase of friction coefficient, the recovery capacity of the support decreases with the increase of friction coefficient.
finite element; hysteretic curve; critical displacement; residual displacement
10.15916/j.issn1674-3261.2022.01.011
TU391
A
1674-3261(2022)01-0056-04
2020-12-28
辽宁省高校基本科研项目(JFL201715402)
陈章伟(1995-),男,陕西西安人,硕士生。
董锦坤(1969-),男,辽宁凌海人,教授,博士。
责任编辑:孙 林

