基于多边形膜片弹簧与压电致动器复合的一体化主被动Stewart减振系统

2021-10-20 02:28王敏吴军卫蒲华燕孙翊彭艳谢少荣罗均丁基恒

航空学报 2021年9期

王敏,吴军卫,蒲华燕,孙翊,彭艳,谢少荣,罗均,2,丁基恒,3,*

1. 上海大学无人艇工程研究院，上海 200444

2. 重庆大学机械传动国家重点实验室，重庆 400044

3. 同济大学上海智能科学与技术研究院，上海 200082

遥感卫星的光学成像是当前不受现实环境和地域限制的空间信息获取的主要手段。其可广泛应用于导航定位、海洋预报、灾难监测和军事侦察等多个领域，在国民经济、军事科技方面起到非常重要的作用。遥感卫星中的主要工作部分是高分辨率镜头，其工作环境的好坏对整个系统影响至关重要。遥感卫星在轨工作时，由于太阳能电板的运转、动量轮的高速转动都会造成高分辨率镜头的微小振动，会使得高分镜头产生米级的成像误差。航空光学设备成像精度的持续增加来源于隔振性能的改善。在很多精密设备的工作环境中，通常将多个单自由度的隔振器以一定的形式并联起来构成6自由度隔振平台，这是较常用的隔振器构型[1-3]。

在多自由度平台中有一种叫Stewart构型的平台广泛应用于航空航天、精密机床、飞行器模拟等精密设备中，其具有精度高、承载能力强等特点[4-5]。北京航空航天大学李伟鹏[6]研制了一种空间高稳定精密更碎Stewart平台，该平台基于“滚珠丝杠+压电陶瓷”复合作动器组成。此种复合执行器式Stewart平台从执行器角度以滚珠丝杠执行器为宏动部分、压电执行器为微动部分的大行程高频响精密复合执行器。其复合执行器作动行程超过50 mm，经微动部分补偿后的整体定位误差小于1 μm。指向机构采用6-SPS并联式Stewart构型,可实现高精度、大范围指向，实验测试也证明其对指向机构具有较高的跟踪精度能力，但其存在抑振能力不足的缺点。比利时布鲁塞尔大学(ULB)研制的“软式”六杆Stewart抑振平台[7]，每根杆上集成主被动混合抑振系统，包含一个音圈电机(集成柔性片)、一个力传感器和两个柔性铰链。它可以有效抑制带宽5～400 Hz的振动信号，在50～200 Hz之间实现最大-40 dB的振动衰减，同样由于其“软”式结构，无法承载较大质量，且无结构保护装置，限制了其使用范围。

Stewart隔振平台主要由负载平台、基础平台以及6条隔振单腿组成[8-9]。Stewart隔振平台主要分为立方体构型和非立方体构型2种，立方体构型的新型Stewart隔振平台相较于非立方体构型平台的优势有：每条腿给整个平台提供的刚度均匀，各方向受力均匀，各条单腿之间的耦合最小，运动学、动力学关系简单，机械结构设计起来简单等[10]。

由于一般线性减振器的刚度是固定的，当刚度较大时具有较强的静载荷能力，但同时其固有频率也较大，其对低频振动的抑制效果就较差；而当刚度较小时，其低频处的减振效果较好，但静载荷能力却较差[11-17]。系统的固有频率不能一味的降低，要根据系统应用场景进行调整。为了解决减振器的这一矛盾，本文提出了一种具有高静刚度低动刚度特性的多边形膜片弹簧。其可以根据被减振物体的实际重量来设计膜片弹簧的参数，从而得到能满足减振需求的膜片弹簧。

然而，仅仅靠膜片弹簧减振有个很明显的缺点，其只能起到隔振作用，减振系统在共振峰处的峰值还是较大[18-23]。为了削弱共振峰值，给膜片弹簧串联一个压电致动器和力传感器。并采用基于天棚阻尼的比例积分力(PIF)反馈控制算法进行控制。天棚阻尼算法能够有效克服在低频隔振性能与高频高衰减性能之间的矛盾，其不仅可有效降低固有频率处共振峰的幅值，而且能够保证高频的高衰减性的隔振性能；而本文中基于天棚阻尼的PIF反馈控制算法，不仅可以实现天棚阻尼的效果，而且能够依靠比例环节改变系统的负载质量矩阵系统，从而进一步降低系统固有频率。

被动减振系统能够有效降低高频的振动，但是对于低频和固有频率附近处却无能无力，此处的振动信号不仅无法得到衰减，反而会共振放大。主动反馈控制能够有效解决固有频率处信号被放大这个问题，即共振峰衰减的问题。与传统的相对阻尼反馈控制相比，采用绝对阻尼反馈的天棚阻尼(Sky-Hook Damping)技术能够有效克服在低频减振性能与高频高衰减性能之间的矛盾，其不仅可有效降低固有频率处共振峰的幅值，而且能够保证高频的高衰减性的减振性能。然而，天棚阻尼技术却无法改变减振系统的固有频率和主动减振带宽的问题。众所周知，固有频率的降低和主动减振带宽的拓宽能够有效提高系统的减振性能。

本文综合考虑传统的Stewart平台，采用具有明显优势的立方体构型Stewart平台，在单腿结构上创新性的采用具有高静刚度低动刚度并加上压电执行器和力传感器使之具有主动抑制能力。相较于现有的减振方案，本文所提方法有以下创新性：

1)提出一种基于Stewart构型的新型减振装置，降低了装置复杂程度。

2)采用新型多边形膜片弹簧，使系统固有频率明显前移，使之具有较强隔振能力。

3)采用主动执行器运用控制算法，整个系统固有频率处的共振峰将明显下降，使之减振能力进一步加强。

1 隔振器的构型及组成

图1为本文所设计的Stewart型隔振器的三维模型。其主要由4部分组成：① 航空高分镜头；② 上平台(负载平台)；③ 单杆隔振单元；④下平台(基础平台)。其中单杆隔振单元长度为94 mm，上下平台布局根据立方体排布的6个单杆隔振单元来限定。对于多自由系统，不同方向的振动会互相耦合，为此，有必要对平台进行解耦处理。对这种6自由度Stewart平台进行解耦可以通过将平台设计成立方体构型来解决[24]。所谓立方体构型就是6条单腿在空间上组成一个立方体，相邻2条单腿在空间上互相垂直。这样一来就能将多自由度求解问题转换成了多个单自由度的求解问题[25]。立方体构型使得Stewart隔振平台的结构得到简化，各条单腿之间的耦合性低，整个隔振平台各向的隔振性能更加统一。

图1 隔振器三维模型Fig.1 3D model of vibration isolator

图2为单腿隔振单元，其包含：① 柔性铰链；② 压电陶瓷；③ 多边形膜片弹簧；④ 力传感器；⑤ 柔性铰链。其中起隔振作用的关键部件就是多边形膜片弹簧，柔性铰链具有高轴向刚度和低弯曲和扭曲刚度的特点，可以有效克服间隙和摩擦，能保证单腿在整个隔振平台中只提供轴向的力。

图2 单杆隔振单元Fig.2 Single leg vibration isolation unit

2 多边形膜片弹簧的设计

作为隔振器的关键元件，多边形膜片弹簧的性能与隔振器的性能直接相关。本文采用静力学方法对多边形膜片弹簧进行分析，建立起力学及刚度模型。图3为本文所设计的多边形膜片弹簧三维模型。图中带有圆孔的面为弹簧的上面和下面，这2个面通过螺栓、螺母与杆件连接从而组成隔振单腿。膜片弹簧的厚度为h，宽度为b，多边形每条边的长度为Li(i=1,2，…，8)。

图3 多边形膜片弹簧三维模型Fig.3 3D model of polygonal diaphragm spring

将多边形膜片弹簧的6条边看成是弯曲杆，则整个膜片弹簧的总刚度则由所有的弯曲杆等效刚度串并联而成。由于弹簧的上面和下面较厚，因此将上下面等效成刚性面。图4(a)为膜片弹簧的等效模型，整个膜片弹簧的刚度由杆件L1-L7所对应的轴向等效刚度k1-k7组成。由于整个机构呈左右对称设计，如图4(b)所示,取左半部分进行具体的分析，左半部分的总刚度K1由等效刚度k1、k2、k3组成，根据刚度的串联原理其关系可表示为

图4 膜片弹簧原理图Fig.4 Schematic diagram of diaphragm spring

(1)

整个膜片弹簧的等效刚度K为左半部分等刚度K1与右半部分等效刚度K2并联而成：

K=K1+K2=2K1

(2)

如图4(b)所示，膜片弹簧的等效刚度k1由杆件L1弯曲形成，等效刚度k2由杆件L2轴线拉压形成，等效刚度k3由杆件L3弯曲形成，Δy为受载荷力L4在Y方向的位移量，Fx1，Fy1分别为L1在X，Y方向上的受力大小,Fx2，Fy2分别为L2在X，Y方向上的受力大小，Fx3，Fy3分别为L3在X，Y方向上的受力大小，α为L1/L3膜片与水平方向夹角。由于整个机构上下也对称，即杆件L1与L3的性质完全相同，因此首先将杆件L1单独拿出来分析，如图5所示。图中Δx1，Δy1分别为L1在X，Y方向上的位移变化量；α为L1膜片与水平方向夹角；θ为角α的变化量。

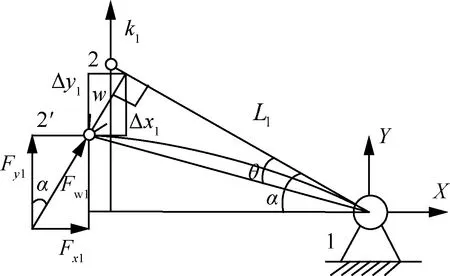
图5 杆件L1的受力分析图Fig.5 Stress analysis diagram of bar L1

实心矩形截面的惯性矩为

(3)

悬臂梁在受到静载荷Fw1下的挠度w为

(4)

转角为

(5)

悬臂梁在受到静载荷Fw1作用下，当梁的转角很小时，点2在Y方向上的位移可近似为Δy1：

(6)

式中：E为材料的弹性模量；I为实心矩形截面的惯性矩。根据式(6)可得，弯曲梁在单腿轴向的等效刚度k1就是梁的弯曲刚度k在Y方向上的分量：

(7)

图6为左半部分膜片弹簧工作时的力位移曲线。Fcr为杆件L2的欧拉临界载荷。当负载小于Fcr时，杆件L2不弯曲可以看成是一个刚体，此时只有L1和L3起隔振作用，膜片弹簧整体刚度相对较大，能承受较大静载荷。由于L1和L3刚度相同，他们串联后的刚度为k1/2。而当负载大于Fcr时，此时杆件L2开始弯曲，不再看成是一个刚体，即杆件L2此时进入隔振工作状态，此时膜片弹簧的总刚度由杆件L1、L2、L33个刚度串联而成如式(1)所示。此时，膜片弹簧的整体刚度较小。研究设计的工作状态就是负载大于Fcr后的区间，此时整个膜片弹簧的刚度较小，这意味着隔振系统的固有频率较低，具有较宽的隔振带宽[26-27]。

图6 膜片弹簧的力位移曲线(左半部分)Fig.6 Force-displacement curve of diaphragm spring (left half)

图7为侧边杆件L2受力分析图，曲杆在受到载荷力F后在Y方向上表现出弹性特性，可作为隔振器的弹性元件。整个杆件看成是一个抗弯刚度为EI的弯曲梁，L为梁件的初始长度，Δy2为上端点在Y方向上的位移，F为轴向载荷，梁在y处沿X轴方向的挠度为w(y)。

图7 侧边杆件L2受力分析图Fig.7 Force analysis diagram of side bar L2

梁弯曲后平衡状态描述为[28]

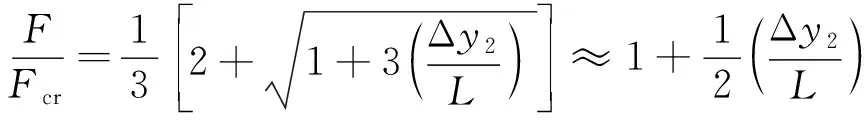
(8)

式中：Fcr为欧拉临界载荷。将式(8)两边各乘Fcr可得

(9)

由于Fcr为常数，其与材料性质以及梁形状有关，因此此弯曲梁L2的刚度为

(10)

由于整个膜片弹簧呈上下对称设计，则梁L3的刚度以及位移特性与梁L1相同。左半边膜片弹簧的总刚度由梁L1、L2、L3的3个刚度k1、k2、k3串联而成，将式(7)和(10)代入式(1)中得到左半部分膜片弹簧的刚度为

(11)

将式(11)代入式(2)得，整个膜片弹簧的等效刚度为

(12)

从上面的分析可以得知，当整个系统处于静止或者微小振动时，其刚度是较大的，能够很好地承受很大的质量；当整个系统处于较强振动时，即整个系统运动行程超过图6所示的Fcr/k1时，系统刚度较低，即降低了装置的固有频率，达到了隔振效果。

3 采用PIF反馈控制算法的简化模型

基于天棚阻尼控制技术，结合本文设计的并联式减振结构，采用动态力传感器与压电执行器的组合，设计PIF主动减振控制算法来对并联式减振平台进行主动振动控制。PIF不仅可以通过增加比例环节改变系统的负载质量矩阵系统，从而有效降低系统的固有频率；而且可以通过积分环节改变系统的阻尼，形成天棚阻尼效果，从而保证高频高衰减率的同时抑制谐振峰处的振动幅值，实现了变质量矩阵和天棚阻尼的双重效果。

根据前文中提出的结构，设计单自由度PIF反馈控制的原理简图如图8所示。在图8中，压电致动器由压电伸长量δ表示。单自由度PIF反馈控制的主动振动控制方式为：动态力传感器采集到动态力的信号，经过去噪声干扰滤波后，在主动控制单元中完成比例积分(PI)计算补偿后，将控制信号传递给压电致动器，完成主动控制。其中，PI控制器(M·Γ·s+M·Ψ)/kηs由一个增益为kp=M·Γ的比例控制器(Γ为比例增益补偿器)和一个增益为ki=M·Ψ的积分控制器(Ψ为积分增益补偿器)组成,M为负载质量。

图8 单自由度PIF反馈控制的原理简图Fig.8 Schematic diagram of single degree of freedom PIF feedback control

天棚阻尼的控制律和基于天棚阻尼技术的PIF的控制律分别为

(13)

(14)

式中：Λ为天棚阻尼技术的增益系数；kp=M·Γ为PIF反馈控制的比例增益系数；ki=M·Ψ为PIF反馈控制的积分增益系数。

根据图8所示，单自由度PIF反馈控制隔振系统的运动控制方程为

Ms2xo=-ms2xi=kη(xi-xm)=F

(15)

δ=xo-xm

(16)

式中:x0为负载的位移量;xi为基础扰动位移量;xm为中间段位位移量。

压电致动器的伸长量δ和力传感器的输出量F之间的开环传递函数可表示为

(17)

根据式(14)中PIF算法的比例增益系数和PIF算法的积分增益系数，进行整理计算可得中间段位移xm为

(18)

单自由度结构隔振系统在分别采用传统天棚阻尼控制算法和PIF反馈控制算法下的传递率函数分别为

(19)

(20)

其中:c为系统阻尼值，当增益系数Λ≫c,Ψ≫c时，隔振系统的等效阻尼可被忽略。

根据式(19)和式(20)所示，将采用不同控制方式的仿真曲线绘制如图9所示。图中，红线为质量M=1.7 kg，刚度kη=9.79×104N/m，阻尼c=69 N·s/m的被动隔振系统的传递率曲线；绿线为采用绝对速度反馈的天棚阻尼主动控制技术的传递率曲线；蓝线为采用PIF主动反馈控制的传递率曲线。从图中曲线可以看出，天棚阻尼技术不仅能够抑制固有频率处的共振峰幅值，而且能够维持被动隔振系统在高频的高衰减性，高频的传递斜率可达到-40 dB/decade。进一步地，PIF反馈控制在保证天棚阻尼技术的优势后，能够进一步的降低隔振系统的固有频率，使得固有频率前移，隔振带宽拓宽，隔振性能进一步提高。

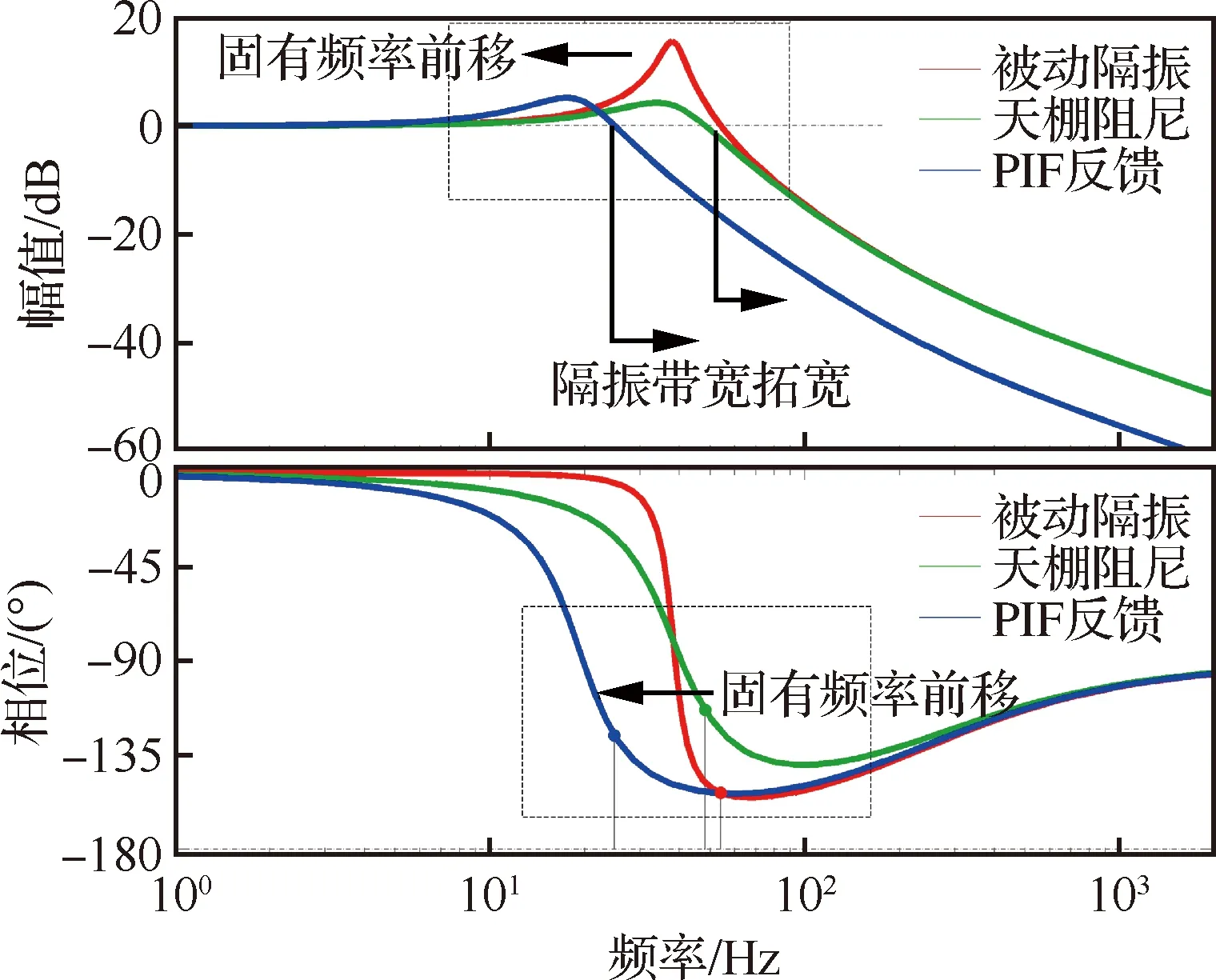
图9 采用天棚阻尼反馈与PIF反馈控制的传递率仿真对比曲线Fig.9 Simulation comparison curve of Sky-Hook Damping feedback and PIF feedback control

采用PIF反馈控制后新形成的主动隔振系统与原始被动隔振系统相比，系统的阻尼和固有频率之间的关系变为

(21)

(22)

式中：ωn为原被动隔振系统的固有频率；ε为隔振系统的阻尼比；ωc为采用PIF反馈控制后的主动隔振系统的固有频率。

根据式(21)和式(22)可知，采用PIF反馈控制后的主动减振系统的固有频率取决于比例增益补偿器Γ，阻尼则依赖于积分增益补偿器Ψ。因此，隔振系统的闭环刚度系统的闭环刚度与比例增益成反比、闭环阻尼与积分增益成正比。反馈回路中采用的力传感器加PI控制器，构成的PIF反馈控制，等同于增加系统的质量矩阵和营造出天棚阻尼的效果。因此，PIF反馈不仅可以保证固有频率处的共振峰峰值衰减和高频的高衰减率，而且还可以改变系统的固有频率。

4 基于天棚阻尼的PIF反馈控制仿真分析

根据图8所示的单自由度PIF反馈控制的原理简图，通过雅库比矩阵计算将单自由度问题转换成整个Stewart平台的多自由度问题后进行仿真分析。一个1.7 kg的负载质量块被添加到Stewart平台的上端，下端放置一个1.1 kg的基础质量块，构成一个多自由度系统的负载平台与基础平台。减振系统在Z方向上的等效刚度为9.79×104N/m。此时，系统的固有频率为36.8 Hz，系统的阻尼经过大致计算约为69 N·s/m，其他方向上的值也相同。将采用PIF反馈控制的单自由度系统在开环和不同参数的闭环情况，在MATLAB中进行传递率曲线仿真对比分析，采用不同控制参数的PIF反馈控制的传递率曲线和采用不同控制参数的PIF反馈控制的时域图分别如图10和图11所示。将图10和图11中所采用的仿真参数及仿真结果数值列举在表1中。

表1 PIF反馈控制的仿真参数及仿真结果

从图10可以看出，随着不同反馈增益系数Γ和Ψ的增大，主动控制效果越明显，固有频率下降越明显，从36.8 Hz降低至15.9 Hz，共振峰幅值衰减越有效果，从16.1 dB降低至4.91 dB。同样从图中也可以看出，随着反馈增益系数Γ和Ψ的增大，负载平台的时域信号也得到不断的衰减，从±0.6g降低至±0.07g，振动衰减达88%。

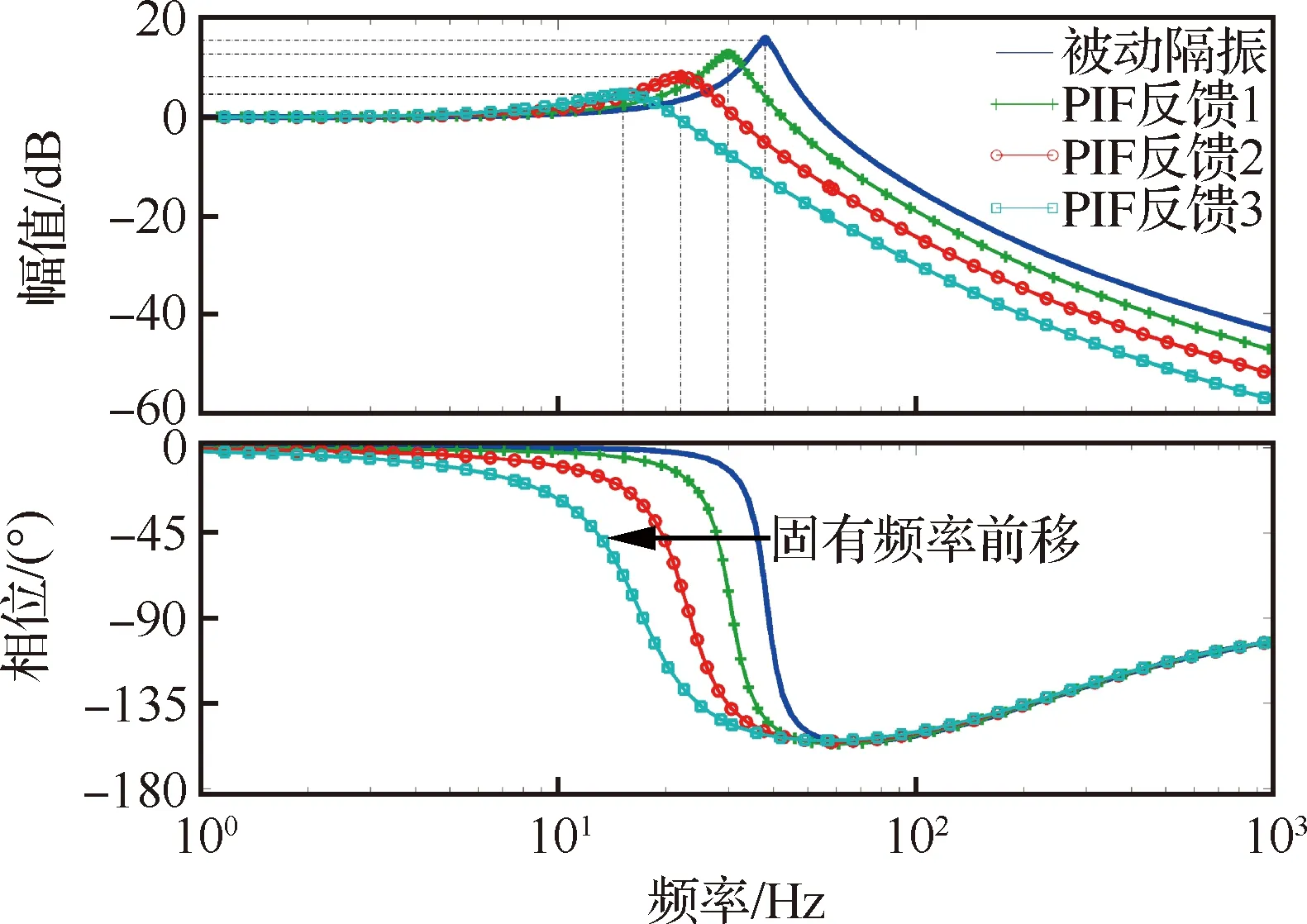
图10 不同控制参数的PIF反馈控制传递率曲线对比图Fig.10 Comparison of transfer rate curve of PIF feedback control with different control parameters

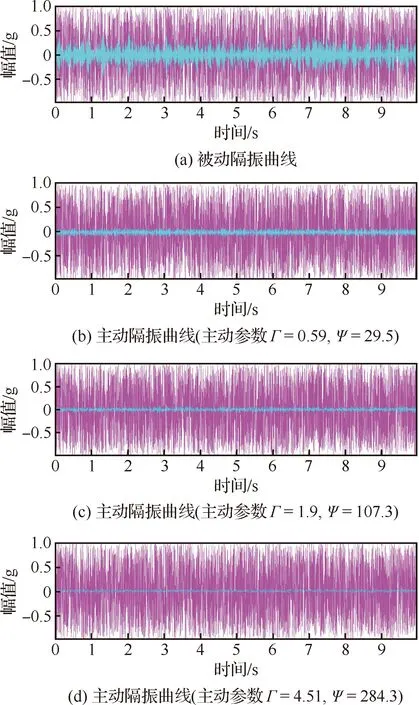
图11 不同控制参数的PIF反馈控制时域对比曲线图Fig.11 Comparison curve of PIF feedback control with different control parameters in time-domain

5 结论

1) 本文提出了一种基于Stewart构型的多自由度主被动复合减振器方案，确定了减振器的构型及主被动减振元件组成，大大降低了此结构的复杂程度。

2) 根据减振器高静-低动特性的需求，确定了减振器的关键原件膜片弹簧的工作原理，确定了膜片弹簧的构型，建立了膜片弹簧的刚度模型。