基于并矢格林函数法的孔径缝隙激励矩形波导场研究

雒向东，张 明，海 波

(兰州城市学院 电子与信息工程学院，甘肃 兰州 730070)

1 基本理论

1.1 直角坐标系的矢量波函数

20世纪30年代中期，汉森首先引进了矢量波函数用来解决某些电磁问题，其后斯特莱顿验证了这些函数的有效性，认为矢量波函数是构成各类并矢格林函数本征函数展开式的积木块.汉森引进的L、M、N3类矢量波函数都满足齐次亥姆霍兹矢量方程[1-2].因为磁型并矢格林函数M、N既满足矢量波动方程又具有无散性[3]，所以将它们作为积木块来研究孔径缝隙激励的矩形波导辐射场问题较为方便.

直角坐标系表示的矩形波导如图 1 所示，领示矢量c为z轴正向单位矢量，这样可构成两组矢量波函数M和N，分别表示矩形波导理论中的TE模和TM模.

矢量波函数M和N在波导壁上满足矢量狄里克莱边界条件：

n×M=0，

n×N=0.

这一边界条件相当于在一个纯导体表面上电场应满足的条件.

矩形波导内电磁场的直角坐标系矢量波函数可取如下形式[4]71-75:

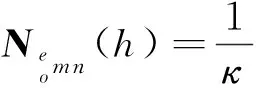
1.2 波函数的正交性

直角坐标系矢量波函数具有如下正交性[4]71-75：

它对奇偶函数的任何组合都成立，且

m、n、h和m′、n′、h′可以不同或相同，代表两组本征值.体积分区间为:

x⊂[0,a],y⊂[0,b],z⊂(-∞,+∞).

当m≠m′或n≠n′时，有：

由此可见，所有直角坐标系矢量波函数都是相互正交的.

当m=m′和n=n′时，设h≠h′，归一化系数讨论如下：

对n=0，证明有以下相同结论：

(1)

克罗内克符号定义为：

(2)

同样可推得：

(3)

对Nemn和Nomn函数可用同样方法求得的归一化系数为：

(4)

(5)

2 孔径隙缝激励的波导场

2.1 矢量函数Aemn(h)和Bomn(h)的确定

当用沿波导壁的孔径或隙缝场激励波导时，可用下式计算波导内部的场[4]74：

因为

(6)

函数定义域为:

0≤x≤a, 0≤y≤b, -∞≤z≤∞，

并在x=0、x=a、y=0、y=b满足第一类磁型并矢格林函数的边界条件:

假设

(7)

其中,Aemn(h)和Bomn(h)为两个待定的未知矢量函数.用函数Mem′n′(-h′)作为前标积，取本征值m′、n′、h′，可得：

(8)

将式(8)左边积分分成两项：

由于径向R′位于体积V内，上式中面积分等于零，故得：

当m=m′、n=n′时，式(8)右边积分为:

可得:

解出的系数为:

上式也可写为:

将本征值上的撇号去掉，但函数N′上的撇号不能去掉，上式改写为：

从而得到式(7)中的未知系数Aemn(h).用类似方法将Nom′n′(-h′)与式(7)作为前标积，用同样程序可推证得：

(9)

2.2 系数a(h)和b(h)的确定

假设

(10)

将式(9)和式(10)代入式(6)，利用下式:

可推得：

(11)

将式(11)代入式(10)，得:

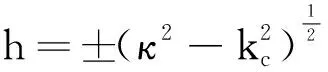
其中,上行符号对应z>z′,下行符号对应z

当用波导壁的孔径或隙缝场激励波导时，波导内部的场由下式确定：

3 结 语

采用并矢格林函数方法处理电磁场问题始于20世纪40年代初，史文格、莱文、戴振铎等采用这种方法求解各类电磁场边值问题和各类复杂媒质中的电磁场问题，使格林函数方法成为了处理电磁场问题的一种系统理论和有效方法.本文基于并矢格林函数法对矩形波导由孔径或缝隙激励时波导内场的确定进行了理论分析，推得的公式对波导内场结构研究和波导设计等具有重要的理论意义.