由Lévy过程驱动的随机线性二次最优控制问题

武灿文,唐矛宁

(1.浙江师范大学 数学与计算机科学学院,浙江 金华 321004；2.湖州师范学院 理学院,浙江 湖州 313000)

随机微分方程是随机分析中的研究重点,在随机控制问题中具有广泛的应用.关于不连续鞅驱动的倒向随机微分方程问题,Tang、Li于1994年得到了由泊松点过程驱动的倒向随机微分方程解的存在唯一性[1].一般来说,Lévy过程没有鞅表示定理.2000年,Nualart、Schoutens引入了一类特殊的Lévy过程,它是与Lévy过程相关联的成对强正交Teugel’s鞅[2],2001年,又给出了Teugel’s鞅驱动的倒向随机微分方程相适应解的存在唯一性[3].之后,又有学者对Teugel’s鞅驱动的倒向随机微分方程进行了研究.

随机线性二次最优控制问题是最优控制问题中的一个重要类型,也称为SLQ问题.2008年，Mitsui首次提出了关于Teugel’s鞅下的SLQ问题，并证明在一维情况下,倒向随机Riccati微分方程解的存在唯一性[4]；2009年,Tang、Wu证明了一类广义随机Riccati方程的可解性是最优控制存在的一个充分条件[5],Meng、Tang首次建立了Teugel’s鞅驱动的非线性正向随机系统的随机极大值原理和验证定理[6]；2012年，Tang、Zhang获得了倒向随机系统的相应结果,并将其应用于线性二次最优控制问题[7]，Meng、Zhang等研究了在部分信息下由Lévy过程驱动的倒向随机系统的最大值原理[8]；2014年，Zhang、Tang等研究了Teugel’s鞅驱动的非线性正倒向随机系统的最优控制问题,并得出了相应的理论结果[9]；2015年，Wang、Huang研究得到了由Lévy过程驱动的完全耦合的正倒向随机控制系统的随机最大值原理,并利用随机最大值原理求解LQ问题[10]；2016年，Sun、Li等研究了一类具有确定系数的SLQ最优控制问题开环和闭环的可解性,其结果对线性二次问题的内部结构有了新的认识[11].

文献[6]利用随机最大值原理解决了系统由Teugel’s鞅和布朗运动共同驱动的SLQ最优控制问题.本文在此基础上将系统拓展到更一般的情况:该系统不仅由Teugel’s鞅和布朗运动共同驱动,且状态方程中存在漂移项,性能指标中含有交叉项.

1 记号与准备工作

设T是一个给定的正实数,(Ω,F,F,P)为完备的概率流空间.其中，F={Ft}0≤t≤T是一族由一维标准布朗运动{W(t),0≤t≤T}与Lévy过程{L(t),0≤t≤T}生成且右连续递增的完备子σ-代数流.设{L(t),0≤t≤T}是一个独立于布朗运动{W(t),0≤t≤T}的R-值Lévy过程,且L有下列特征函数形式：

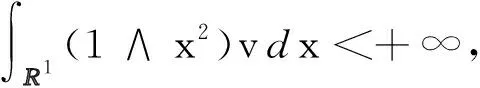
Ft=σ(W(s),s≤t)∨σ(L(s),s≤t)∨N,

其中，N为概率P下的全体零测集.

Hi(t)=ci,iY(i)(t)+ci,i-1Y(i-1)(t)+…+ci,1Y(1)(t),

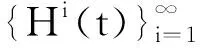
下面介绍本文中用到的一些基本符号:

E:关于概率P的期望.

l2:Hilbert空间中所有实值序列x={xn}n≥0,满足

E|ξ|2<∞.

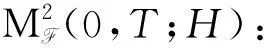
L2(Ω,F,P;H):(Ω,F,P)中的H-值随机变量ξ的集合,满足

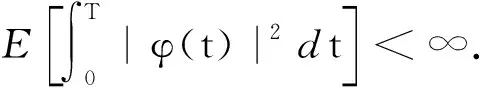
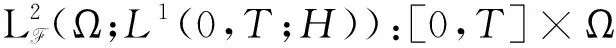
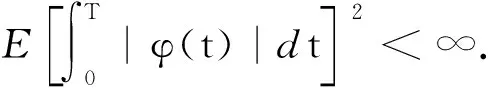
2 问题的提出

考虑如下由布朗运动和Teugel’s鞅共同驱动的线性随机微分方程(SDE):

(1)

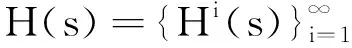
二次性能指标定义为:

(2)

对任意的可允许控制过程u(·),系统(1)相应的强解记为X(x,u)(·)或X(·),称X(·)为一个可允许的状态过程,(u(·),X(·))为允许对.

本文研究的随机线性二次(SLQ)最优控制问题可描述为：

问题1找到一个可允许控制u*(·)∈U[0,T],使得

(3)

成立.

任意满足上述关系的u*(·)∈U[0,T]称为问题1的最优控制过程,对应的状态过程X*(·)称为最优状态过程,相应的(u*(·),X*(·))称为问题1的最优对.当b(·),σ(·),βi(·),g(·),q(·),ρ(·)=0时,相应的性能指标记作J0(x;u(·)).

下面给出本文的基本假设：

假设1状态方程的系数:

A(·):[0,T]→Rn×n;B(·):[0,T]→Rn×m;C(·):[0,T]→Rn×n;D(·):[0,T]→Rn×m;Ei(·):[0,T]→Rn×n,i=1,2,…;Fi(·):[0,T]→Rn×m,i=1,2,…

都是一致有界的可测函数.另有：

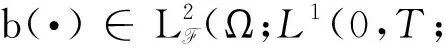
假设2性能指标的权重系数:

Q(·):[0,T]→Sn;S(·):[0,T]→Rm×n;R(·):[0,T]→Sm,

都是在[0,T]上一致有界的.另有：

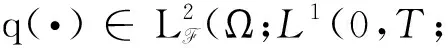
存在δ>0,更确切地有：

G≥0,R(s)≥δI,Q(s)-S(s)TR-1(s)S(s)≥0,s∈[0,T].

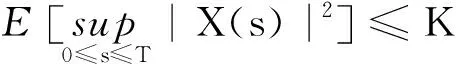
(4)

|J(x;u(·))|<∞.

(5)

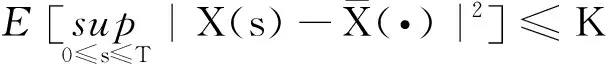
(6)

因此,由引理1可以断言问题1定义良好.

3 最优控制的存在唯一性

引理2若假设1和假设2成立,则性能指标J(x;u(·))在U[0,T]上是连续的.

(7)

引理3若假设1和假设2成立,则性能指标J(x;u(·))在U[0,T]上是严格凸的.进一步,性能指标函数J(x;u(·))在U[0,T]上是强制的,即

证明由凸函数的定义易得J(x;u(·))在U[0,T]上是严格凸的,且有：

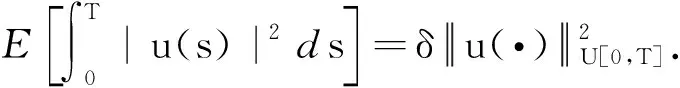
(8)

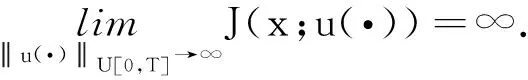
引理4若假设1和假设2成立,则性能指标J(x;u(·))在U[0,T]上Frèchet可导,对应的Frèchet导数J′(x;u(·))由以下公式给出：

(9)

其中，X(x,u)(·)为状态方程(1)的解,X(0,v)(·)为如下状态方程的解.

(10)

证明设u(·),v(·)为两个任意给定的可允许控制过程,记式(9)右端为Δu,v.由于状态方程(1)是线性的,易证X(x,u+v)(s)=X(x,u)(s)+X(0,v)(s),0≤s≤T.由性能指标(2)的定义可得：

J(x;u(·)+v(·))-J(x;u(·))=J0(0;v(·))+Δu,v，

(11)

其中，

因此,

(12)

即J(x;u(·))有Frèchet导数Δu,v.证毕.

(13)

下面给出并证明问题1最优控制的存在唯一性.

定理1若假设1和假设2成立,则问题1存在唯一的最优控制.

证明可允许控制集U[0,T]是一个自反的Banach空间,由本文引理1～3,再参考文献[12]的命题2.12,即可得证(定义在自反的Banach空间上的严格凸的,下半连续且强制的泛函存在一个唯一的最小值点).证毕.

定理2若假设1和假设2成立,则问题1可允许控制u(·)∈U[0,T]为最优控制的充要条件是对任意的可允许控制v(·)∈U[0,T],都有：

〈J′(x;u(·)),v(·)〉=0.

(14)

证明先证必要性:若u(·)∈U[0,T]为最优控制,对任意的可允许控制v(·)∈U[0,T]和0<ε≤1，有：

(15)

同理,〈J′(x;u(·)),-v(·)〉≥0,但由于〈J′(x;u(·)),v(·)〉关于v(·)是线性的,故可得〈J′(x;u(·)),v(·)〉=0.

再证充分性:设u(·)为给定的可允许控制,使得任意可允许控制v(·),有〈J′(x;u(·)),v(·)〉=0.由于性能指标J(x;u(·))在U[0,T]上是凸的,故有：

J(x;v(·))-J(x;u(·))≥〈J′(x;u(·)),v(·)〉=0.

(16)

因此,u(·)为最优控制.

证毕.

4 最优性条件与随机Hamiltonian系统

首先引入关于系统(1)的对偶方程：

(17)

若假设1和假设2成立,由文献[7]中引理2.3可知对偶方程(17)存在唯一解.定义Hamiltonian函数为H:[0,T]×Rn×U×Rn×Rn×l2(Rn)→R,

(18)

则对偶方程(17)也可以改写成如下的随机Hamiltonian系统:

(19)

定理3若假设1和假设2成立,则问题1可允许控制对(u(·),X(·))为最优对的充要条件为(u(·),X(·))满足

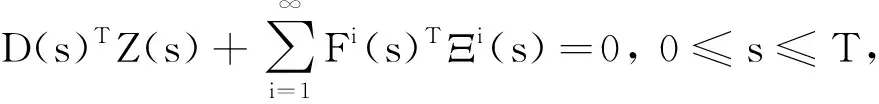
(20)

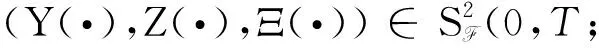
证明先证必要性:设(u(·),X(·))为最优控制对,(Y(·),Z(·),Ξ(·))为最优对(u(·),X(·))对应的对偶方程(17)的唯一解,由文献[6]中定理5.1建立的最大值原理，可得:

Hu(s,X(s-),u(s),Y(s-),Z(s),Ξ(s))=0, 0≤s≤T.

(21)

由Hamiltonian函数(18)的定义,即可得式(21),因此必要性成立.

(22)

对式(22)两边同时取期望再移项,带入式(9)可得:

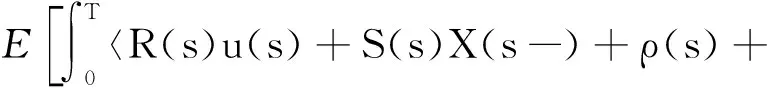
(23)

若式(20)成立,则〈J′(x;u(·)),v(·)〉=0,由定理2,(u(·),X(·))为最优控制对,故充分性成立.

证毕.

接下来介绍由状态方程(1)、对偶方程(17)和对偶刻画(20)组成的随机Hamiltonian系统：

(24)

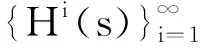
5 Riccati方程与最优控制的状态反馈表示

5.1 Riccati方程的推导

假设状态过程X(·)与对偶过程Y(·)具有以下关系：

Y(s)=2[P(s)X(s)+η(s)], 0≤s≤T.

(25)

其中，P(·)为确定性可微函数,η(·)为随机可微函数,使得它们分别满足

(26)

和

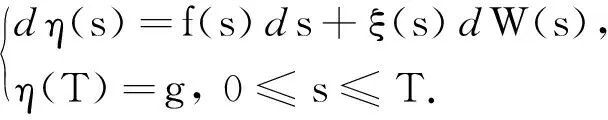
(27)

(28)

对比上式与方程(17)中 dY(s)的扩散项和漂移项,有:

(29)

和

(30)

把式(25)与式(29)代入式(20),可得：

(31)

(32)

再将式(25)、式(29)、式(32)代入式(30),有：

(33)

令

(34)

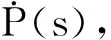
(35)

其中，M、N为式(34)所示.再由式(27)得，(η(·)、ξ(·))为如下倒向随机微分方程的解.

(36)

5.2 最优控制的状态反馈表示

定理4若假设1和假设2成立.设P(·)为Riccati方程(35)的唯一解,(η(·),ξ(·))为方程(36)的唯一适应解.对任意的(s,x)∈[0,T]×Rn,SLQ问题唯一开环可解,最优控制u*(·)的状态反馈形式为：

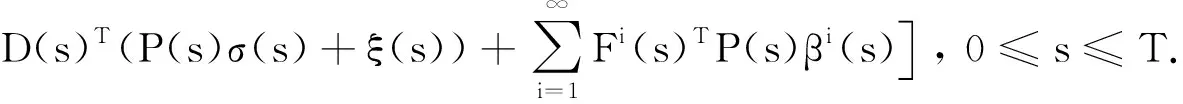
(37)

其中，M、N为式(33)所示.

证明设P(·)为Riccati方程(35)的唯一解,(η(·),ξ(·))为方程(36)的唯一适应解,则如下闭环系统存在唯一解X*(·),其中u*(·)为式(37)所示.

(38)

假设如下倒向随机微分方程存在唯一解(Y*(·),Z*(·),Ξ*(·)),

(39)

定义

(40)

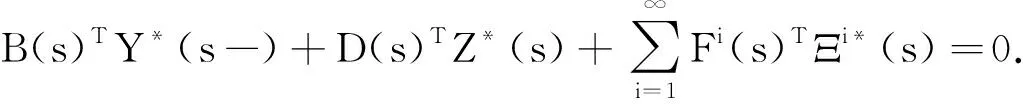
(41)

因此,由定理3知u*(·)为对应的最优控制,(u*(·),X*(·),Y*(·),Z*(·),Ξ*(·))为随机Hamiltonian系统(24)的解.

证毕.

6 Riccati方程解的存在唯一性

在文献[13]中已经得知Riccati方程的可解性对问题1的解至关重要.本节主要证明Riccati方程解的存在唯一性.

定理5若假设1和假设2成立,则对任意的s∈[0,T],问题1是唯一可解的,当且仅当对应的Riccati方程(35)是唯一可解的.

定理6若假设1和假设2成立,P(·)∈C(0,T;Rn×n)是Riccati方程(35)的解,则P(·)是唯一解.

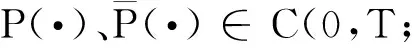
(42)

其中，M(s)、N(s)为式(34)所示.另外

(43)

M′(s)、N′(s)定义为:

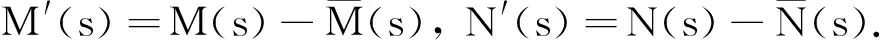
(44)

将式(43)与式(44)代入方程(42),可得：

(45)

定理7若假设1和2成立,则Riccati方程(35)在[0,T]上存在唯一解.

为证明此定理,首先需要化简Riccati方程(35).有如下命题:

命题1若假设1和假设2成立,则Riccati方程(35)等价于

(46)

其中，

(47)

N(s)·φ(s)=M(s).

另外，由式(47)得：

(48)

把式(48)代入Riccati方程(35),再由φ(s)的定义便可得到命题1的等价性.证毕.

命题2考虑如下线性矩阵值微分方程：

(49)

证明由于方程是线性的,且系数都一致有界,则存在唯一解P∈C(0,T;Sn).下面令φ(·)为如下随机微分方程的解

(50)

(51)

因为〈Hi(s),Hj(s)〉=δijs,所以对上式两边同时取期望,再化简可得：

(52)

证明(定理7)为说明方程(46)解的存在性,首先构造如下迭代格式:

对j=0,1,2,…,令

(53)

其中，

(54)

令Pj+1(s)为如下方程的解：

(55)

若假设1和假设2成立,则由命题2有Pj(s)≥0,∀0≤s≤T,j≥1.

再证

Pj(s)≥Pj+1(s),∀0≤s≤T,j≥1.

(56)

定义△j(s)=Pj(s)-Pj+1(s),∧j=φj(s)-φj-1(s),由式(53)中的定义,有：

(57)

因此，

(58)

故有：

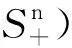
因此,由定理4和定理5知,对任意s∈[0,T],问题1存在唯一的状态反馈表示.

7 结 语

本文研究在一般情况下由布朗运动和Teugel’s鞅共同驱动的随机线性二次最优控制问题，利用凸变分原理,对偶技术等建立随机Hamiltonian系统与Riccati方程，并证明了相应的Riccati方程解的存在唯一性,从而得到了最优控制的唯一反馈表达式.该系统是在有限区间内考虑的,后续研究将会进一步考虑无限区间的随机控制问题.