关于不定方程x3-1=709qy2的正整数解

张 雪，瞿云云，徐 彬

(1.贵州师范大学数学科学学院，贵州 贵阳 550001； 2.武昌首义学院基础科学部，湖北 武汉 430064)

1 引言及主要结论

设Z，N*分别表示所有整数以及正整数的集合，D>0，且D中不含有平方因子.方程

x3-1=Dy2，x，y∈Z

(1)

对于任意给定的数r(r∈N*)，r可以唯一地表示成

r=st2，s，t∈N*，s无平方因子.

(2)

设A(r)=s，B(r)=t.本文主要讨论当D=709q，q≡1(mod 12)为奇素数时，方程

x3-1=709qy2，x，y∈N*

(3)

解的情况，即证明如下定理1和推论1.

定理1 方程(3)有正整数解的充要条件是q适合

q=A(3×7092a4+2 127a2+1)，a∈N*.

(4)

当q适合条件(4)时，方程(3)有正整数解

(x，y)=(1+2 127a2，3aB(3×7092a4+2 127a2+1)).

(5)

推论1 如果q满足以下条件之一，则方程(3)无正整数解：

(ⅰ)q=12k2+12k+1，k∈N*；

(ⅱ)q=108k2±12k+1，k∈N*；

(ⅲ)q=12k2+1，k∈N*；

2 关键性引理

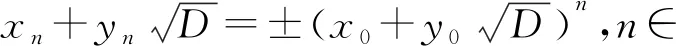
引理2[6]若p是一个奇质数，那么方程4x4-py2=1除了p=3，x=y=1和p=7，x=2，y=3这2组正整数解外，没有其他的正整数解.

引理3[6]方程x2-3y4=1仅有整数解(x，y)=(±2，±1)，(±7，±2)，(±1，0).

引理4[6]若p是一个奇质数，那么方程x4-py2=1除了p=5，x=3，y=4和p=29，x=99，y=1 820这2组正整数解外，没有其他的正整数解.

引理5[7]设k>1，l>1(k，l∈Z)为给定的数，(k，l)=1，kl不是平方数.若不定方程

kx2-ly2=1

(6)

(7)

引理6 如果(x，y)是方程(3)的1组正整数解，则必有

x-1=2 127a2，x2+x+1=3qb2，y=3ab，gcd(a，b)=1，a，b∈N*.

(8)

证明从方程(3)可知(x-1)(x2+x+1)=709qy2，而d=gcd(x-1，x2+x+1)=gcd(x-1，(x-1)2+3(x-1)+3)=gcd(x-1，3)=1或3.

当d=1时，方程(3)有以下4种可能的分解：

(Ⅰ)x-1=709qa2，x2+x+1=b2，y=ab，gcd(a，b)=1，a，b∈N*；

(Ⅱ)x-1=a2，x2+x+1=709qb2，y=ab，gcd(a，b)=1，a，b∈N*；

(Ⅲ)x-1=qa2，x2+x+1=709b2，y=ab，gcd(a，b)=1，a，b∈N*；

(Ⅳ)x-1=709a2，x2+x+1=qb2，y=ab，gcd(a，b)=1，a，b∈N*.

当x和y满足(Ⅰ)式时，由4(x2+x+1)-(2x+1)2=3可知，3=4b2-(2x+1)2=(2b)2-(2x+1)2≥2b+2x+1>3，矛盾，故x和y不满足(Ⅰ)式.

当x和y满足(Ⅲ)式时，由a2≡0，1(mod 4)，q≡1(mod 12)可知qa2≡0，1(mod 4).由x-1=qa2可知x=qa2+1≡1，2(mod 4)，则有x2+x+1≡3(mod 4)成立，即有709b2≡3(mod 4).由x2+x+1=709b2可知b为奇数，故b2≡1(mod 4)，则709b2≡1(mod 4)，矛盾，故x和y不满足(Ⅲ)式.

当x和y满足(Ⅳ)式时，由a2≡0，1(mod 4)，709≡1(mod 4)可知709a2≡0，1(mod 4).由x-1=709a2可知x=709a2+1≡1，2(mod 4)，则有x2+x+1≡3(mod 4)成立，即有qb2≡3(mod 4).由x2+x+1=qb2可知b为奇数，故b2≡1(mod 4).由q≡1(mod 12)可知q≡1(mod 4)，则qb2≡1(mod 4)，矛盾，故x和y不满足(Ⅳ)式.

因此，当d=1时，x和y不满足上面4种情况.

当d=3时，方程(3)有以下4种可能的分解：

(Ⅴ)x-1=2 127qa2，x2+x+1=3b2，y=3ab，gcd(a，b)=1，a，b∈N*；

(Ⅵ)x-1=3a2，x2+x+1=2 127qb2，y=3ab，gcd(a，b)=1，a，b∈N*；

(Ⅶ)x-1=3qa2，x2+x+1=2 127b2，y=3ab，gcd(a，b)=1，a，b∈N*；

(Ⅷ)x-1=2 127a2，x2+x+1=3qb2，y=3ab，gcd(a，b)=1，a，b∈N*.

1 418qa2=yn-1.

(9)

xn+2=4xn+1-xn，x0=1，x1=2；

(10)

yn+2=4yn+1-yn，y0=0，y1=1；

(11)

xn+1=2xn+3yn，yn+1=xn+2yn；

(12)

(13)

当n≡0(mod 2)时，由(11)式可知yn≡0(mod 2)，此时由(9)式可知矛盾，故n≡1，3(mod 4).

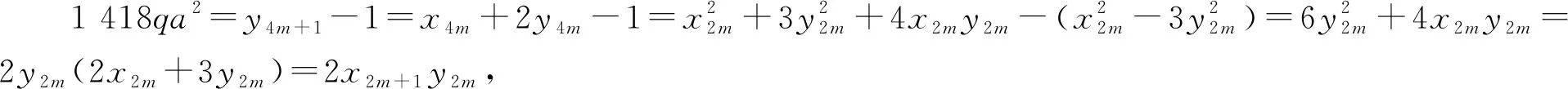
x2m+1=2u2，y2m=1 418qv2，a=2uv，gcd(u，v)=1；

(14)

x2m+1=1 418qu2，y2m=2v2，a=2uv，gcd(u，v)=1；

(15)

x2m+1=1 418u2，y2m=2qv2，a=2uv，gcd(u，v)=1；

(16)

x2m+1=2qu2，y2m=1 418v2，a=2uv，gcd(u，v)=1.

(17)

(15)式中由y2m=2v2与(13)式可得xmym=v2，又gcd(xm，ym)=1，故设xm=c2，ym=d2，gcd(c，d)=1，有(c2)2-3d4=1，由引理3可知c2=1，d=0，即xm=1，ym=0.由(10)和(11)式可知m=0，又q≡1(mod 12)为奇素数，则x2m+1=x1=2≠1 418qu2，因此在该情况下，方程(3)没有整数解.

(16)式中由y2m=2qv2可得xmym=qv2，又gcd(xm，ym)=1，则有以下情形之一成立：

xm=c2，ym=qd2，v=cd，gcd(c，d)=1；

(18)

xm=qc2，ym=d2，v=cd，gcd(c，d)=1.

(19)

将(18)式中的xm=c2和ym=qd2代入X2-3Y2=1中得c4-3(qd2)2=1.由引理4可知d=0，则此时ym=0，即m=0，但x2m+1=x1=2≠1 418u2，因此在该情况下，方程(3)没有整数解.

将(19)式中的xm=qc2和ym=d2代入X2-3Y2=1中得(qc2)2-3d4=1.由引理3可知(q，c，d)=(1，±1，0)，(7，±1，±2)，(2，±1，±1)，当q≡1(mod 12)为奇素数时，(qc2)2-3d4=1无解.因此在该情况下，方程(3)没有整数解.

(17)式中由y2m=1 418v2可得xmym=709v2，又gcd(xm，ym)=1，则有以下情形之一成立：

xm=c2，ym=709d2，v=cd，gcd(c，d)=1；

(20)

xm=709c2，ym=d2，v=cd，gcd(c，d)=1.

(21)

将(20)式中的xm=c2和ym=709d2代入X2-3Y2=1中得c4-3(709d2)2=1.由引理4可知d=0，则此时ym=0，即m=0.由q≡1(mod 12)为奇素数可知x2m+1=x1=2≠2qu2，因此在该情况下，方程(3)没有整数解.

将(21)式中的xm=709c2和ym=d2代入X2-3Y2=1中得(709c2)2-3d4=1，由引理3可知(709c2)2-3d4=1无解，因此在该情况下，方程(3)没有整数解.

x2m+2=709qu2，y2m+1=v2，a=uv，gcd(u，v)=1；

(22)

x2m+2=u2，y2m+1=709qv2，a=uv，gcd(u，v)=1；

(23)

x2m+2=qu2，y2m+1=709v2，a=uv，gcd(u，v)=1；

(24)

x2m+2=709u2，y2m+1=qv2，a=uv，gcd(u，v)=1.

(25)

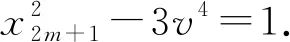
将(24)式代入x2m+2=2x2m+1+3y2m+1得qu2=2x2m+1+3×709v2，即

2x2m+1=qu2-2 127v2.

(26)

因x2m+2≡1(mod 2)，故由(24)式的x2m+2=qu2可知u为奇数，则u2≡1(mod 8).而y2m+1≡1(mod 2)，由y2m+1=709v2可得v是奇数，有v2≡1(mod 8).又x2m+1≡2(mod 8)，故对(26)式两边取模8得4≡q-7(mod 8)，即q≡3(mod 8).又因为q≡1(mod 12)的奇素数对模8的最小非负剩余必为1或5，则矛盾，因此在该情况下，方程(3)没有整数解.

将(25)式代入y2m+1=-x2m+2+2y2m+2得qv2=-709u2+2y2m+2，即

2y2m+2=qv2+709u2.

(27)

因x2m+2≡1(mod 2)，故由(25)式的x2m+2=709u2可知u为奇数，则u2≡1(mod 8).而y2m+1≡1(mod 2)，则由y2m+1=qv2可知v为奇数，则v2≡1(mod 8).又y2m+2≡0，4(mod 8)，故对(27)式两边取模8得0≡q+5(mod 8)，即q≡3(mod 8).又因为q≡1(mod 12)的奇素数对模8的最小非负剩余必为1或5，则矛盾，因此在该情况下，方程(3)没有整数解.

故x和y满足(Ⅴ)式的值仅有(x，y)=(1，0).

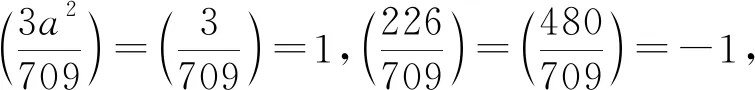
(28)

un+1=6 365 401un+414 060vn，

vn+1=97 856 180un+6 365 401vn

(29)

成立，其中u0=67，v0=1 030.

由(29)式和u0=67，v0=1 030可知，数列{un}中的每一项都为奇数，又因为2b=un与un是奇数相矛盾，故x和y不满足(Ⅶ)式.

因此，当d=3时，若(x，y)是方程(3)的1组正整数解，此时x和y必满足(8)式.

引理7[8]若D(D∈N*)是给定的没有平方因子的数，那么有且只有1组满足

D1D2=D，δ∈{1，2}，gcd(D，δ)=1，(D1，D2，δ)≠(1，D，1)

(30)

的正整数(D1，D2，δ)可使方程

D1U2-D2V2=δ，U，V∈N*

(31)

有解(U，V)，其中正整数组(D1，D2，δ)称为D的Petr组，记作P(D).

3 定理及推论的证明

定理1的证明设(x，y)是方程(3)的1组正整数解，根据引理6可知x和y必满足(8)式.当(8)式成立时，由(x-1)2+3(x-1)+3=x2+x+1可知

3×7092a4+2 127a2+1=qb2.

(32)

根据A(r)及B(r)的定义可知(32)式成立的充要条件是q满足(4)式，所以(8)式成立的充要条件是q满足(4)式.由(8)和(32)式可知，当q满足(4)式时，方程(3)的解满足(5)式.

综上所述，定理1得证.

推论1的证明由定理1可知方程(3)有解的充要条件是q满足(4)式.当q满足(4)式时，q适合(32)式，由3×7092a4+2 127a2+1=qb2可知b只能为奇数，则b2≡1(mod 8).所以由(32)式可得

2a，q≡qb2≡3×7092a4+2 127a2+1≡3(mod 8).

(33)

当q适合推论1中的条件(ⅰ)时，因为q=12k2+12k+1=12k(k+1)+1，此时q≡1(mod 8)，所以由(33)式可知，若此时方程(3)有解(x，y)，则其满足(32)式，从而

q(2b)2-3(1 418a2+1)2=1.

(34)

再由(34)式可知方程

qU2-3V2=1，U，V∈N*

(35)

有解(U，V)=(2b，1 418a2+1).因3q是没有平方因子的正整数，则由引理7可知此时3q的Petr组是

P(3q)=(q，3，1).

(36)

另一方面，q=12k2+12k+1可化为3(2k+1)2-q=2，即方程

3U2-qV2=2，U，V∈N*

(37)

有解(U，V)=(2k+1，1).则由引理7可知，此时3q的Petr组是

P(3q)=(3，q，2).

(38)

由(36)式可知这是不可能的，故当q适合推论1中的条件(ⅰ)时，方程(3)无解.

当q适合推论1中的条件(ⅱ)时，因为q=108k2±12k+1=12k(9k±1)+1，此时q≡1(mod 8)，所以从(33)式可知，若此时方程(3)有解(x，y)，则其满足(32)式，此时同理可得3q的Petr组(36)式.但注意到q=108k2±12k+1可化为3q-(18k±1)2=2，即方程

3qU2-V2=2，U，V∈N*

(39)

有解(U，V)=(1，18k±1).则由引理7可知此时3q的Petr组是

P(3q)=(3q，1，2).

(40)

由(36)式可知这是不可能的，故当q适合推论1中的条件(ⅱ)时，方程(3)无解.

(41)

从(41)式可得Y≡0(mod 2k)，即有1 418a2+1≡0(mod 2k)，则0·a2+1≡0(mod 2)，可知1≡0(mod 2)，矛盾.故当q适合推论1中的条件(ⅲ)时，方程(3)无解.

综上所述，推论1得证.