对偶分裂四元数的表示矩阵的棣莫弗定理
2021-10-18 00:46:54孔祥强赵培臣
东北师大学报(自然科学版) 2021年3期
孔祥强,赵培臣
(菏泽学院数学与统计学院,山东 菏泽 274015)
分裂四元数是非交换的结合代数,且含有零因子、幂零元和幂等元[1-3].文献[4-5]研究了分裂四元数及双曲型交换四元数的极表示.文献[6-7]定义了新的非交换环并给出2阶实矩阵的棣莫弗定理.文献[8-11]研究了对偶四元数表示矩阵及分裂半四元数的棣莫弗定理.有关对偶分裂四元数的研究已取得部分成果[12-16].本文将对偶分裂四元数的研究转化为对其四阶表示矩阵的研究,通过引入极表示,给出对偶分裂四元数表示矩阵的不同形式的棣莫弗定理,同时得到对偶分裂四元数表示矩阵方程的求根公式.
符号R、D、H、HD分别表示实数集、对偶数集、分裂四元数集、对偶分裂四元数集,I4表示4阶实单位矩阵.
1 对偶分裂四元数
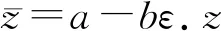
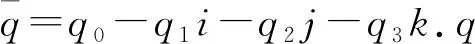
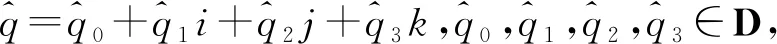
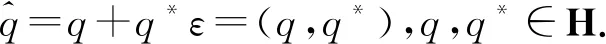
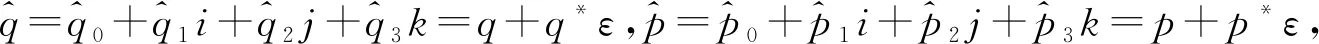

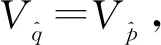
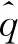
2 对偶分裂四元数的表示矩阵
定理1 任一对偶分裂四元数均可表示为D上的4阶矩阵.
由此可定义对偶分裂四元数集合为D上4阶对偶矩阵集合
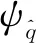
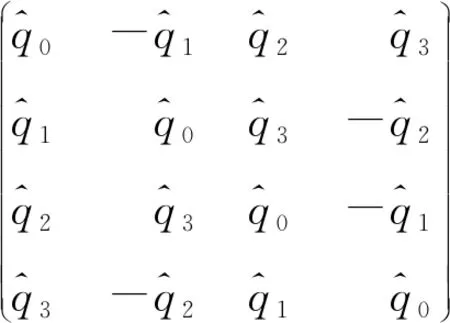
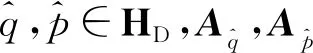
3 对偶分裂四元数表示矩阵的棣莫弗定理
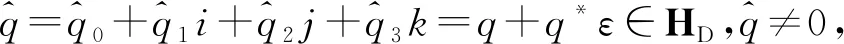
3.1 Nq>0,NVq<0时的情形


证明由数学归纳法,设对任意的正整数n,有
故
又
所以
故对任意的整数n,结论成立.
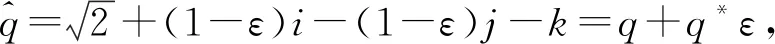
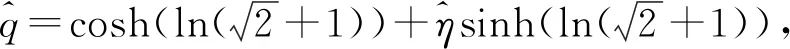
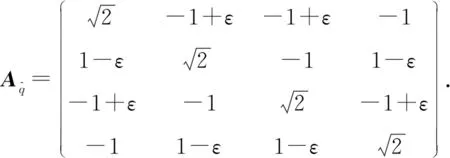
3.2 Nq>0,NVq>0时的情形

则
证明根据归纳法,设对任意的正整数n,有
故
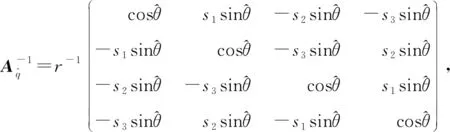

故对任意的整数n,结论成立.
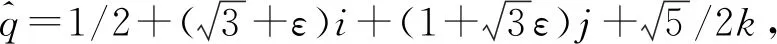
3.3 Nq<0,NVq<0时的情形

且:
(1) 当n为奇数时,
(2) 当n为偶数时,
定理4的证明与定理2—3的方法类似,此处不再赘述.

(1) 当n为奇数时,
(2) 当n为偶数时,
4 对偶分裂四元数表示矩阵的方程的根

其中k为整数.
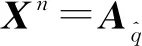
其中k=0,1,2,…,n-1.
当k=0时,第1个根为
当k=1时,第2个根为
依次可求出其余根.
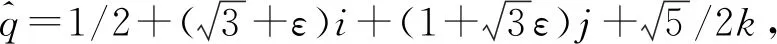
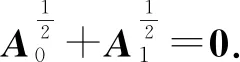
5 结语
对偶分裂四元数及其表示矩阵是四元数领域研究的重要课题.本文从对偶分裂四元数的极表示出发,分3种情形分别介绍了对偶分裂四元数表示矩阵的棣莫弗定理,推广了欧拉公式.当对偶角为实数角时,得到了表示矩阵方程的求根公式.以本文为基础,可进一步研究对偶分裂四元数的其他问题.
猜你喜欢
通化师范学院学报(2022年8期)2022-08-23 07:44:54
中学数学杂志(初中版)(2020年6期)2020-01-06 03:35:20
新教育时代·教师版(2018年17期)2018-07-21 09:39:38
数学大世界(2018年2期)2018-01-27 00:13:17
祖国(2017年21期)2018-01-02 00:55:21
湖州师范学院学报(2016年2期)2016-08-21 13:50:52
应用数学与计算数学学报(2015年1期)2015-07-20 11:39:06
数学年刊A辑(中文版)(2014年4期)2014-10-30 01:50:38
数学年刊A辑(中文版)(2014年6期)2014-10-30 01:41:24
河南科技(2013年18期)2013-08-15 00:48:29

