不确定整数阶分数阶单摆混沌系统的自适应滑模同步
孟 晓 玲
(郑州航空工业管理学院数学学院,河南 郑州 450015)
1 预备知识
分数阶系统同步取得了很多研究成果.[1-9]文献[10]对一类不确定分数阶混沌系统实现了积分滑模同步;文献[11]实现了分数系统主动滑模同步;文献[12]实现了同步时间的估计;文献[13]实现了分数阶不确定Victor-Carmen混沌系统的滑模同步.另一方面,单摆混沌系统引起了众多学者的高度关注.文献[14]研究了整数阶分数阶单摆混沌系统的混沌同步;文献[15]研究了分数阶单摆混沌系统的终端滑模同步.系统的不确定性是影响系统不稳定的根源,另外利用自适应方法研究不确定分数阶单摆混沌系统方面的结果还是比较少的.本文研究不确定整数阶和不确定分数阶单摆系统的自适应滑模混沌同步,给出了不确定整数阶及不确定分数阶单摆混沌系统的自适应滑模同步,通过设计适应律和控制器得到单摆系统获得滑模同步的2个相关结论.
定义1[16-17]分数阶Caputo微分可定义为
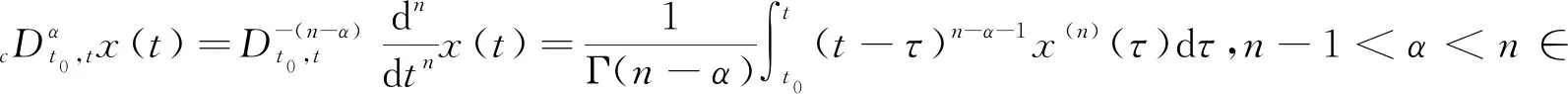
2 主要结果
分数阶单摆系统可以描述为
(1)
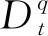
(2)
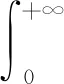
其中:y(t)=(y1,y2)T,[0,+∞)和di(t)为不确定项和外扰,ui(t)代表控制量.
假设1 不确定项Δfi(y)和外扰di(t)均有界,即存在未知常量mi,ni>0,满足
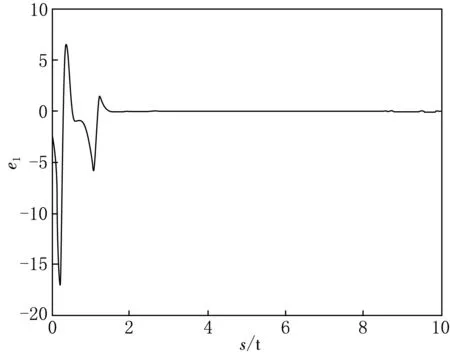
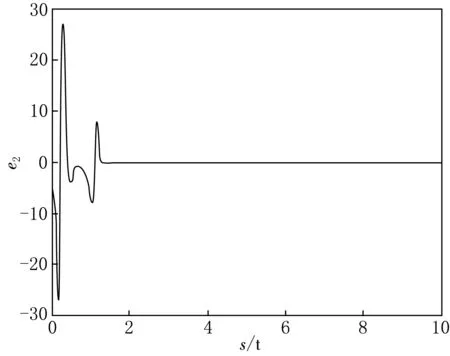
|Δfi(y)| 定义ei=yi-xi(i=1,2),则有 (3) 引理1[18]若x(t)为连续可微的函数,则对任意的t≥0,有 自适应控制律为 从而ei(t)→0,滑模面稳定. 整数阶单摆混沌系统描述如下: (4) 设计(4)为主系统,从系统如下: (5) 定义ei=yi-xi(i=1,2,…,n),从而得 (6) 自适应律设计为 两边积分得 由引理3,得si→0⟹ei(t)→0,则系统(4)与(5)是滑模同步的. 分数阶单摆混沌系统的系统误差如图1—2所示. 图1 第1误差变量 图1 第2误差变量 本文研究了单摆混沌系统的滑模同步,给出了带有不确定性和有界扰动的单摆混沌系统获得滑模同步的结论,设计出新型趋近速度更快的滑模函数是下一步考虑的崭新课题.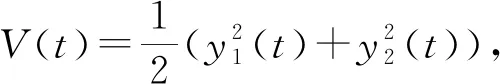
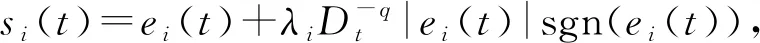
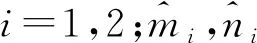
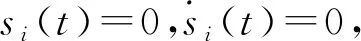
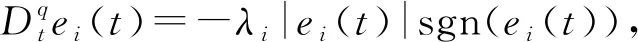
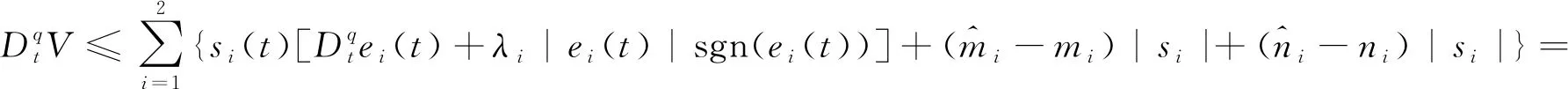
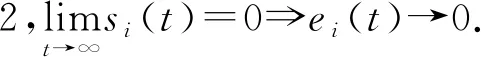
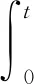
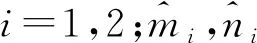
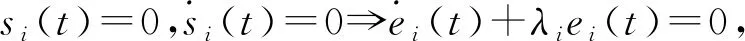
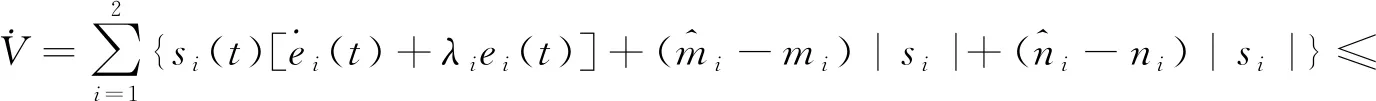
3 数值仿真
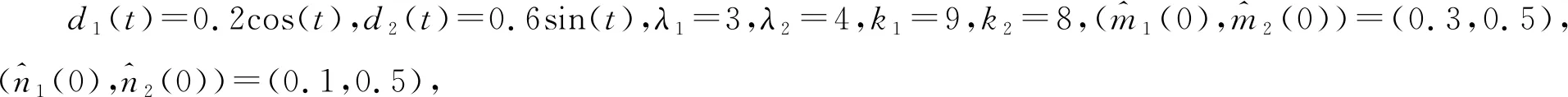
4 结论

